In the figure shown, Find minimum value of i so that TIR never takes place at P.

The correct Answer is:A, B, C
Let us take
Here,
Applying Snell's law at point Q,
Now, we can see that starting from this value of i, we get
If i is increased from this value, then will also increase and decreases from and no TIR takes place at P.
So far no TIR condition i has to be increased from the above value. Or this is the minimum value of i.
Topper's Solved these Questions
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Example Type 10
Explore 1 Video
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Example Type 11
Explore 3 Videos
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
- SEMICONDUCTORSBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORSExercise:Subjective
Explore 12 Videos
Similar Questions
In the figure shown, find .1μ2.

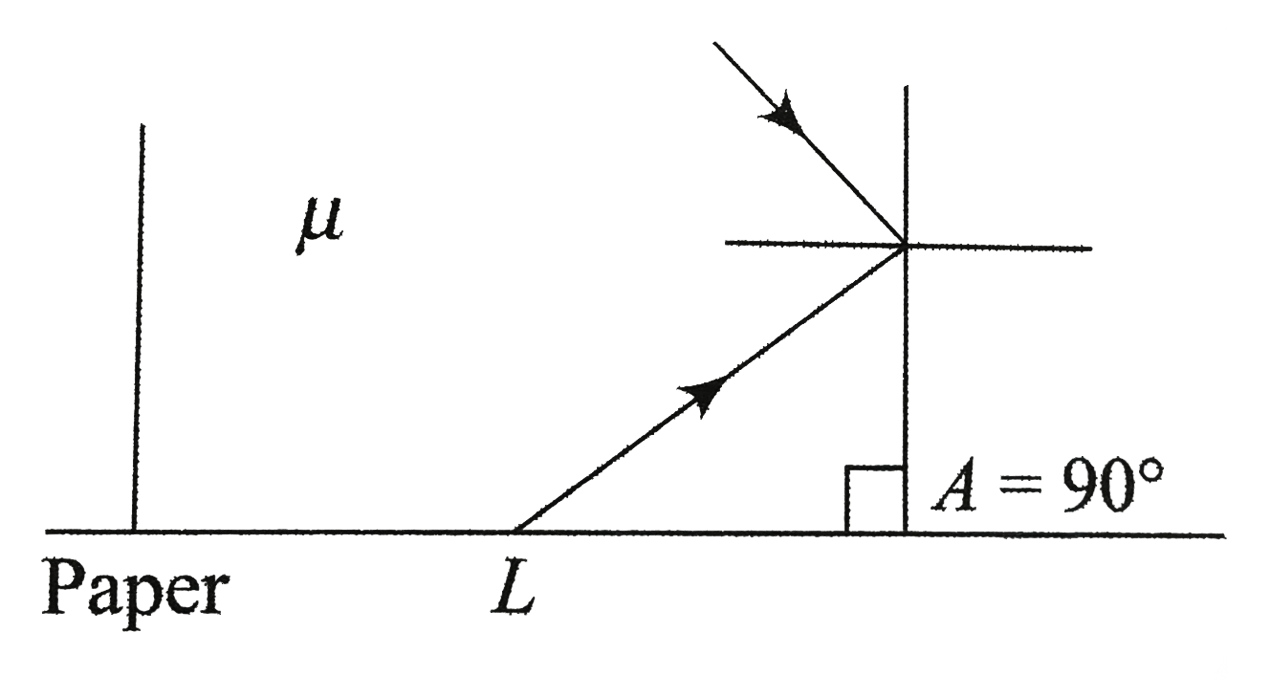
View SolutionA rectangulat block of refractive index μ is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of μ so that the letter L on the page is not visible from any of the vertical sides.
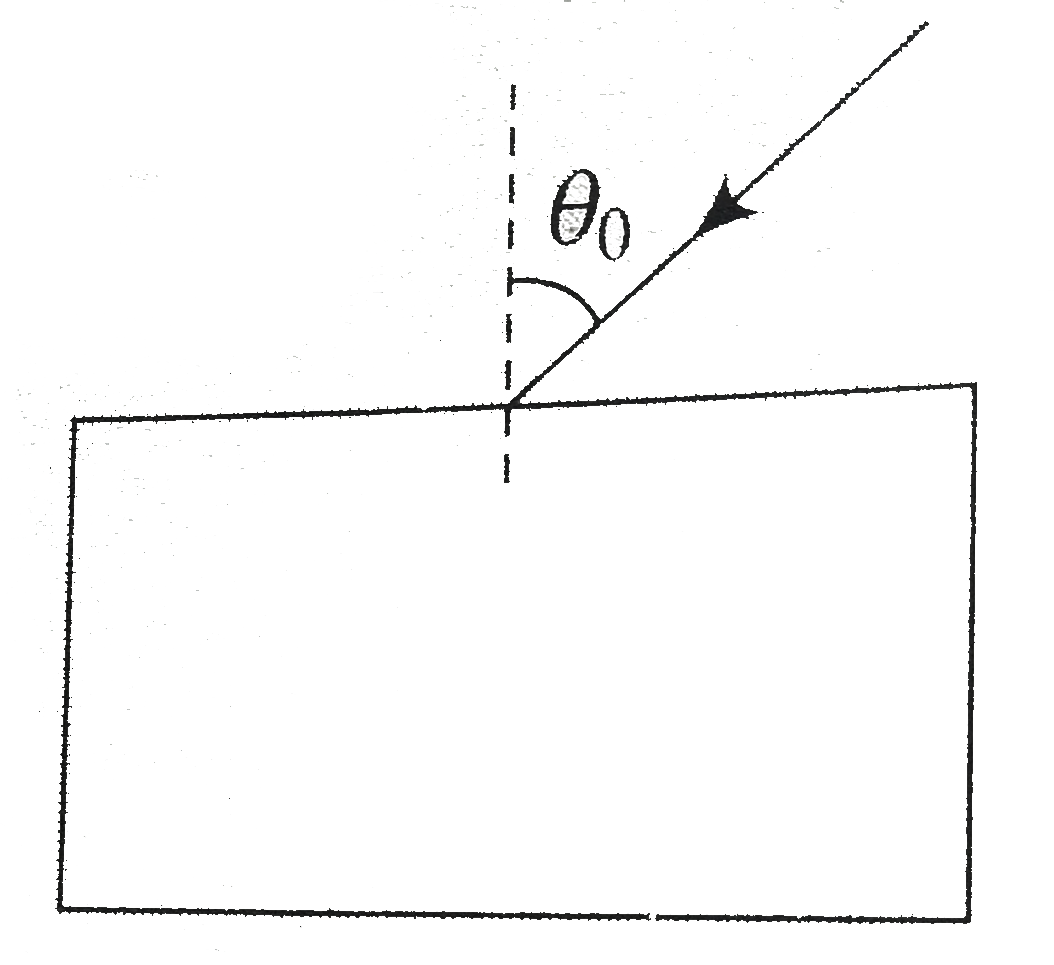
View SolutionA slab of refractive index μ is placed in air and light is incident at maximum angle θ0 from vertical. Find minimum value of μ for which total internal reflection takes place at the vertical surface.
View SolutionIn the figure shown, μ1>μ2>μ3. What are the limits of angle i so that it is neither get total internal reflection at AB nor at CD ?

View SolutionA small block of mass m is projected on a larger block of mass 10m and length l with a velocity v as shown in the figure. The coefficient of friction between the two block is μ2 while that between the lower block and the ground is μ1. Given that μ2>11μ1.

(a) Find the minimum value of v, such that the mass m falls off the block of mass 10m .
(b) If v has minimum value, find the time taken by block m to do so.
View SolutionA glass rod having square cross-section is bent into the shape as shown in the figure. The radius of the inner semi-circle is R and width of the rod is d. Find the minimum value of d/R so that the light that enters at A will emerge at B. Refractive index of glass is μ=1.5

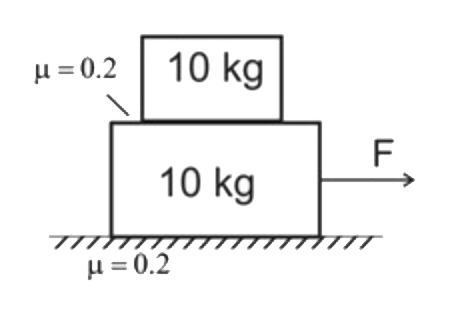
View SolutionInitially, both the blocks are at rest on horizontal surface as shown in the figure. Find the minimum value of force F in (N) so that sliding starts between the blocks (g=10ms−2)
View SolutionInfinite numbers of bloks are placed on a table on a edge as shown in the diagram.
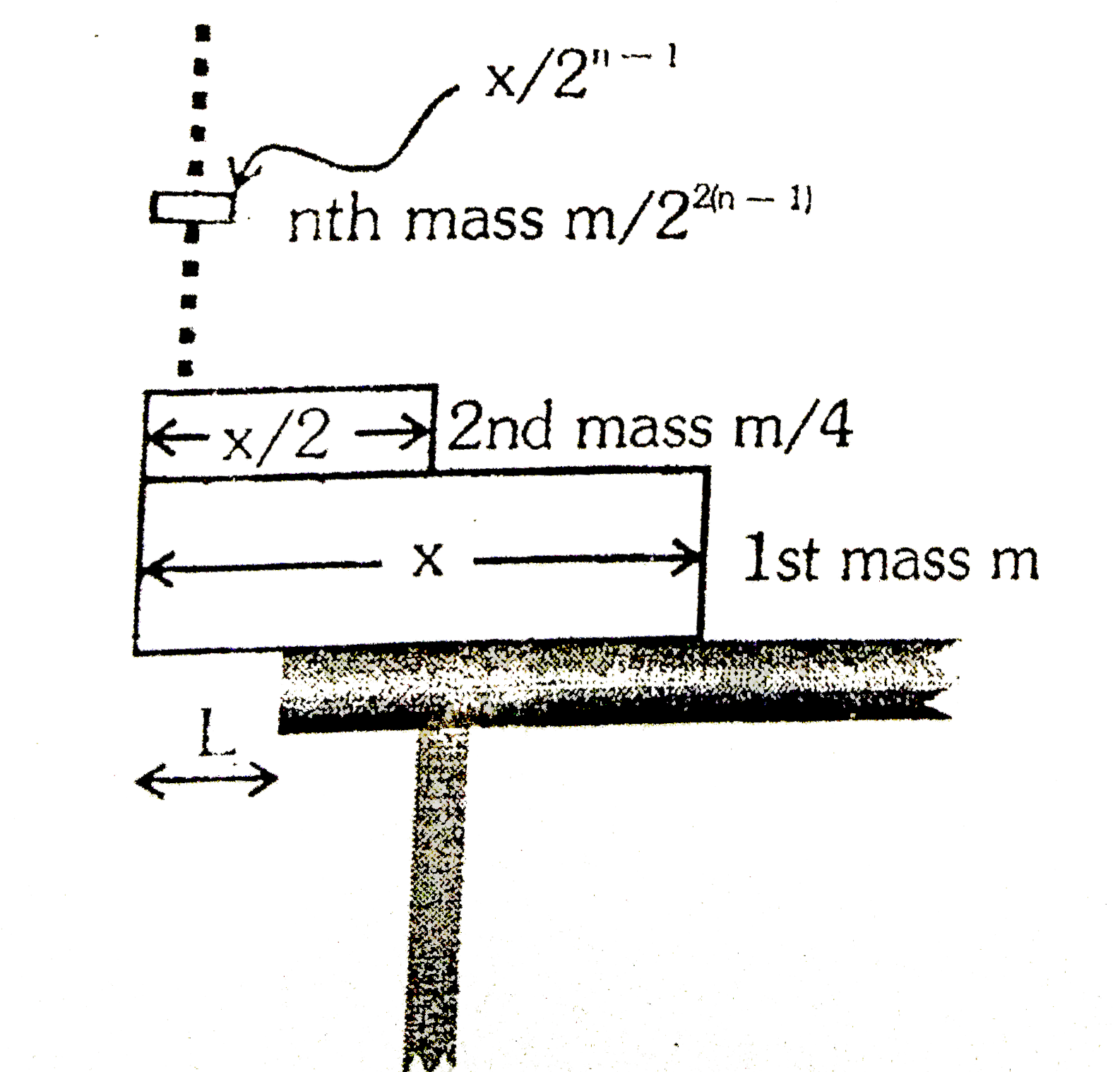
What is the minimum value of L so that the blocks are just going to topple over the table ?
View SolutionThe friction coefficient between the board and the floor shown in figure is μ Find the maximum force that the man can exert on the rope so that the board does not slip on the floor

View SolutionThe refractive index of the material of a prism of refracting angle 45∘ is 1.6 for a certain monochromatic ray. What will be the minimum angle of incidence of this ray on the prism so that no TIR takes place as the ray comes out of the prism.
View Solution
