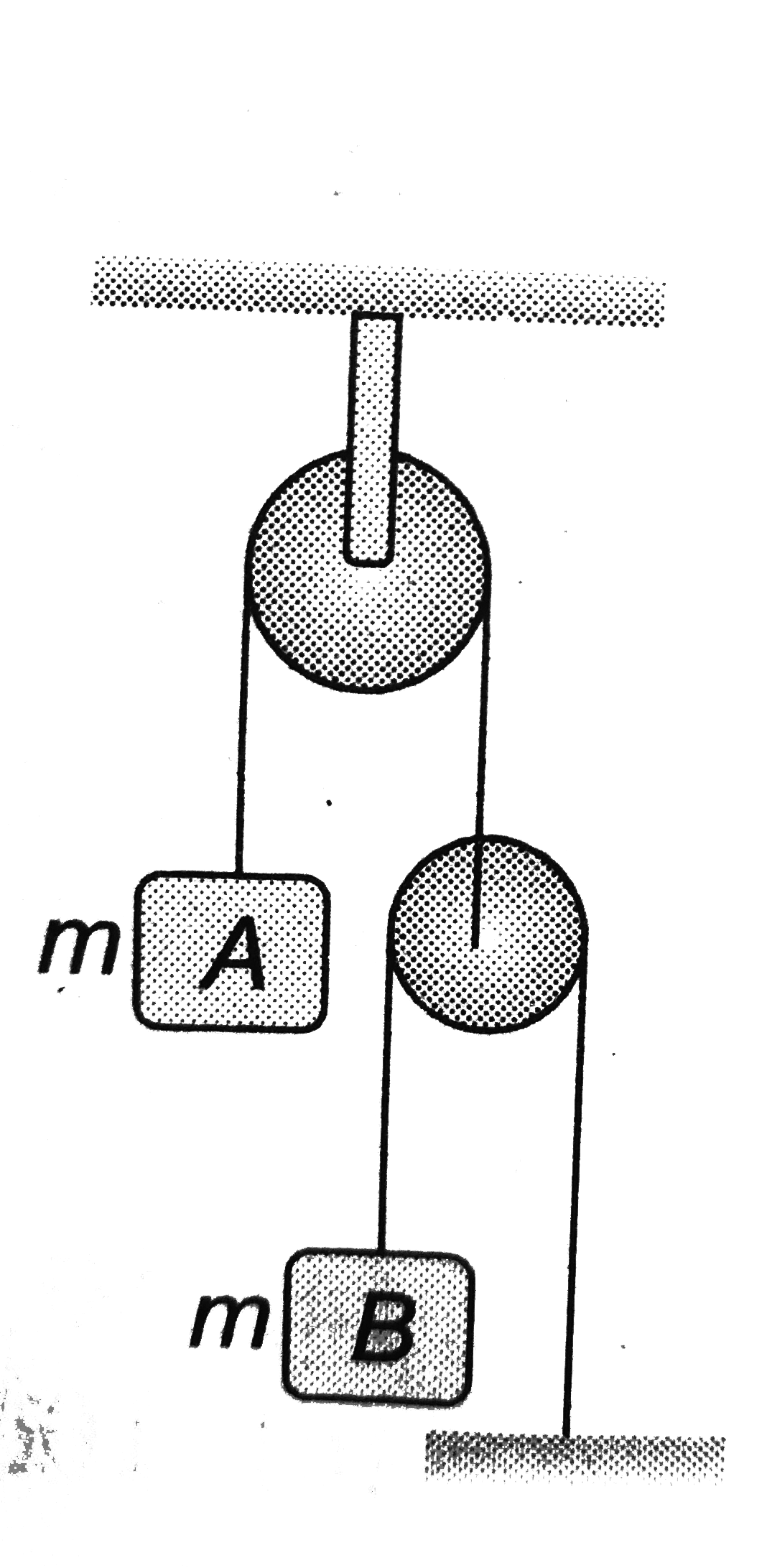
In the figure, the blocks are of equal mass. The pulley is fixed. In the position shown. A moves down with a speed u and vB= the speed of B.
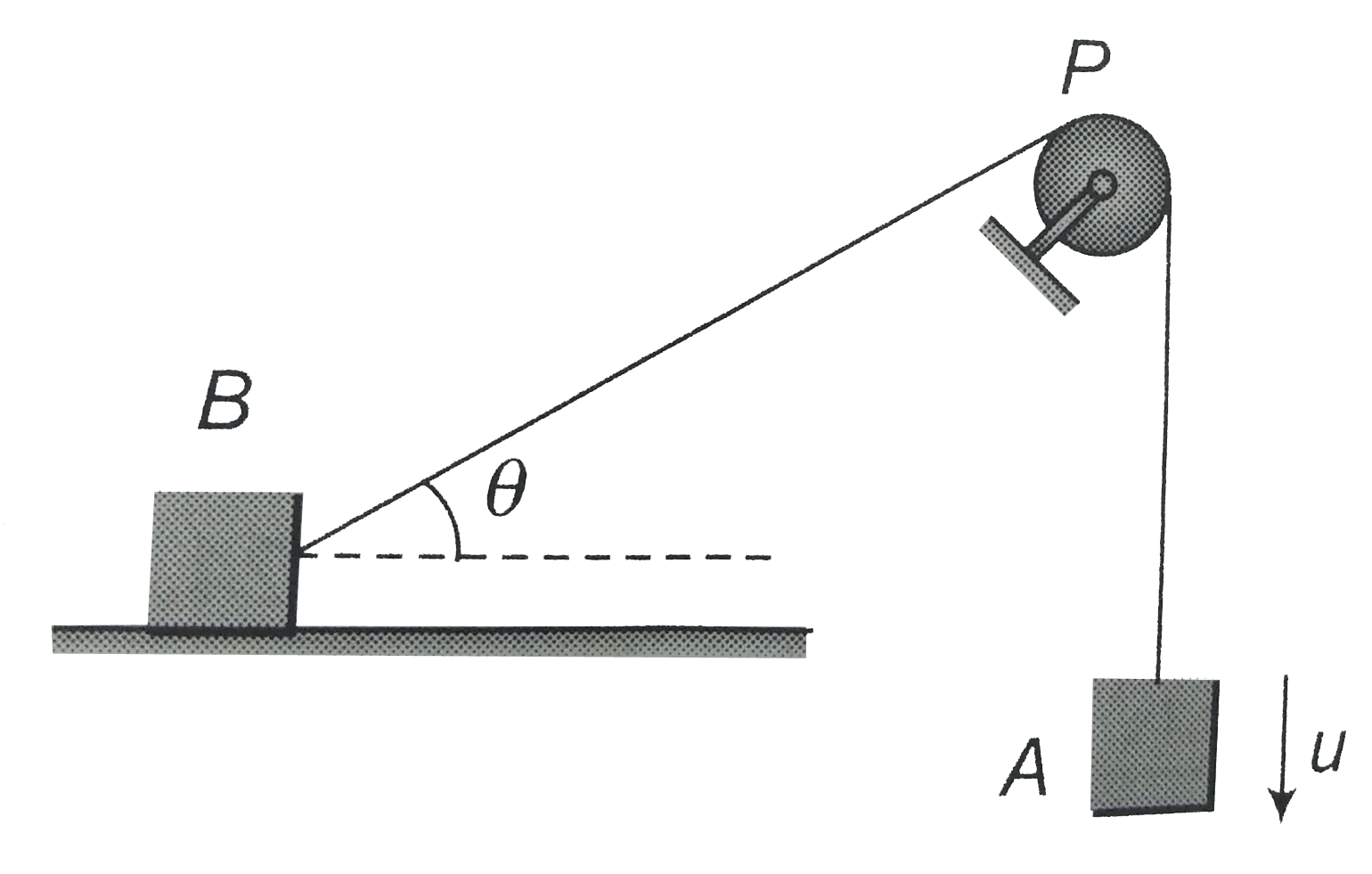
(i) B will never lose contact with the ground.
(ii) The downward acceleration of A is equal in magnitude to the horizontal acceleration of B
(iii) vB=ucosθ (iv) vB=u/cosθ
(i), (ii)
(ii), (iii)
(i),(iv)
(ii),(iv)
The correct Answer is:C
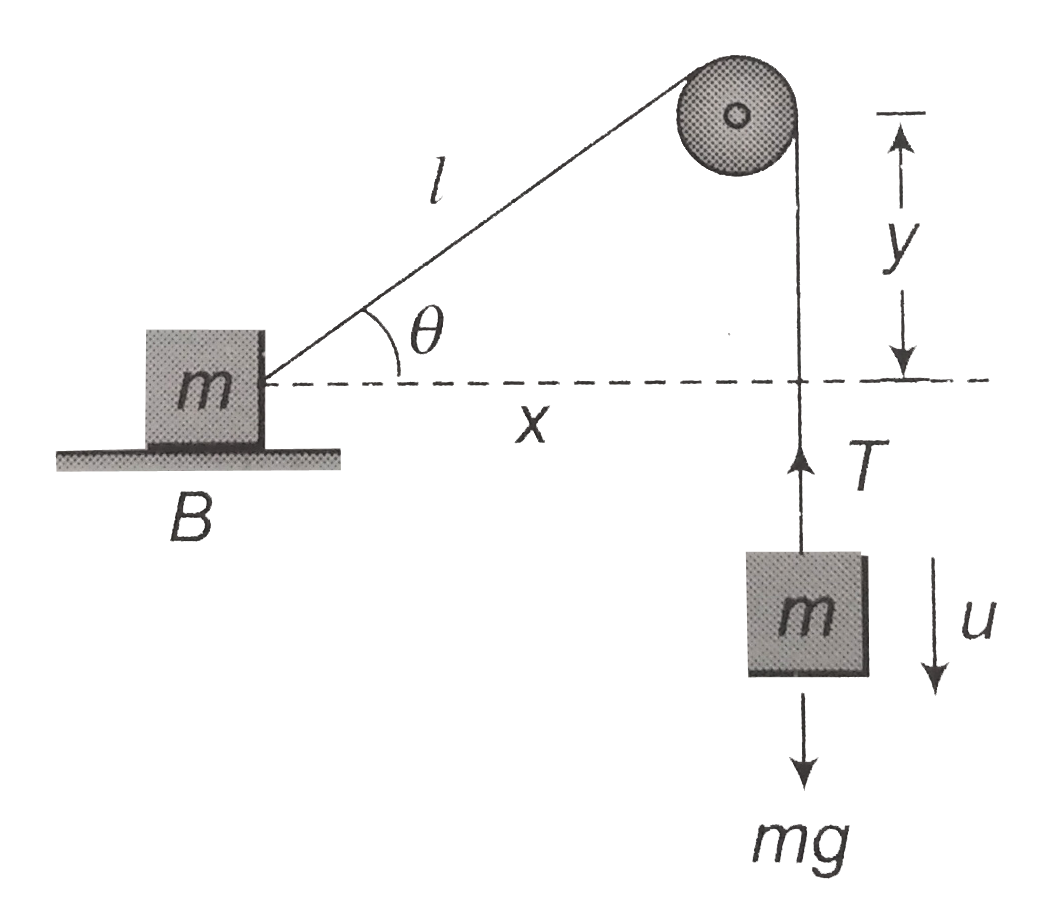
l2=x2+y2
2ldldt+2xdxdt=2ydydt
y is cosntant
ldldt=xdxdt⇒lu=xv0
v0=ux/l=ucosθ

Tsinθ+N=mg since T<mg
N is never zero.
Topper's Solved these Questions
Similar Questions

Two blocks are connected by an inextensible string as shown. The pulley is fixed. If block A moves down with speed v, find the velocit of block B at instant.
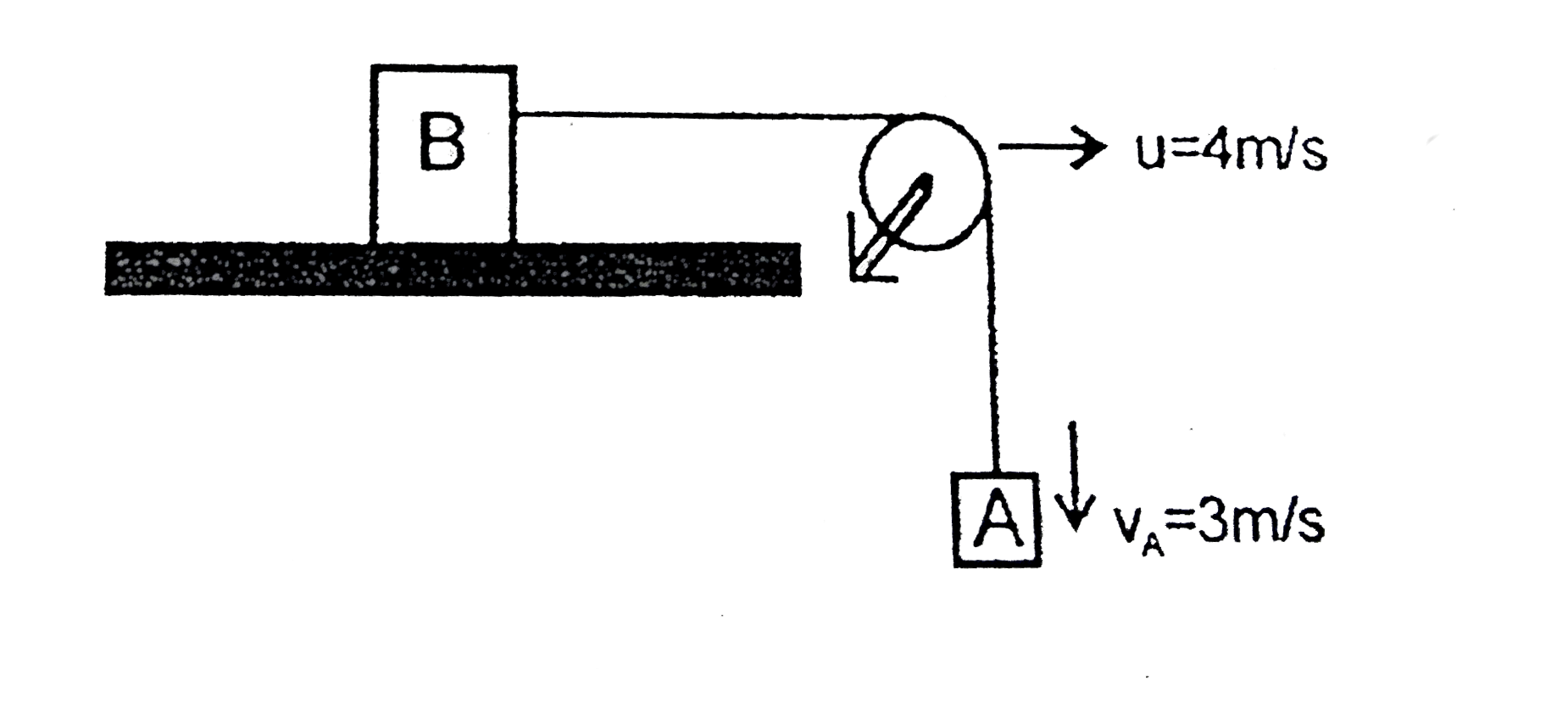
View SolutionIn the figure, the pulley P moves to the right with a constant speed of 4m/s. The downward speed of A is vA=3m/s. Then find the speed of B of the right (in m/s).
View Solution
Knowledge Check
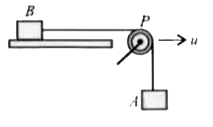
In the figure, the pulley P moves to the right with a constant speed u. The downward speed of A is vA, and the speed of B to the right is vB :
 AvB=u+uABvB+u=vACvA=vBDThe two blocks have acceleration of the same magnitude
AvB=u+uABvB+u=vACvA=vBDThe two blocks have acceleration of the same magnitudeIn the figure, the pulley P moves to the right with a constant speed u. The downward speed of A is vA, and the speed of B to the right is vB.
 AvB=vABvB=u+vACvB+u=vADThe two blocks have accelerations of the same magnitude.
AvB=vABvB=u+vACvB+u=vADThe two blocks have accelerations of the same magnitude.In the figure shown the acceleration of A is, →aA=15ˆi+15ˆj then the acceleration of B is (A remains in contact in B)
 A6ˆiB−15ˆiC−10ˆiD−5ˆi
A6ˆiB−15ˆiC−10ˆiD−5ˆi
In the figure, the pulley P moves to the right with a constant speed u. The downward spee of A is vA and the speed of B to the right is vB . Then,
View SolutionIn the figure shown neglecting friction and mass of pulley, what is the acceleration of mass B ?
View Solution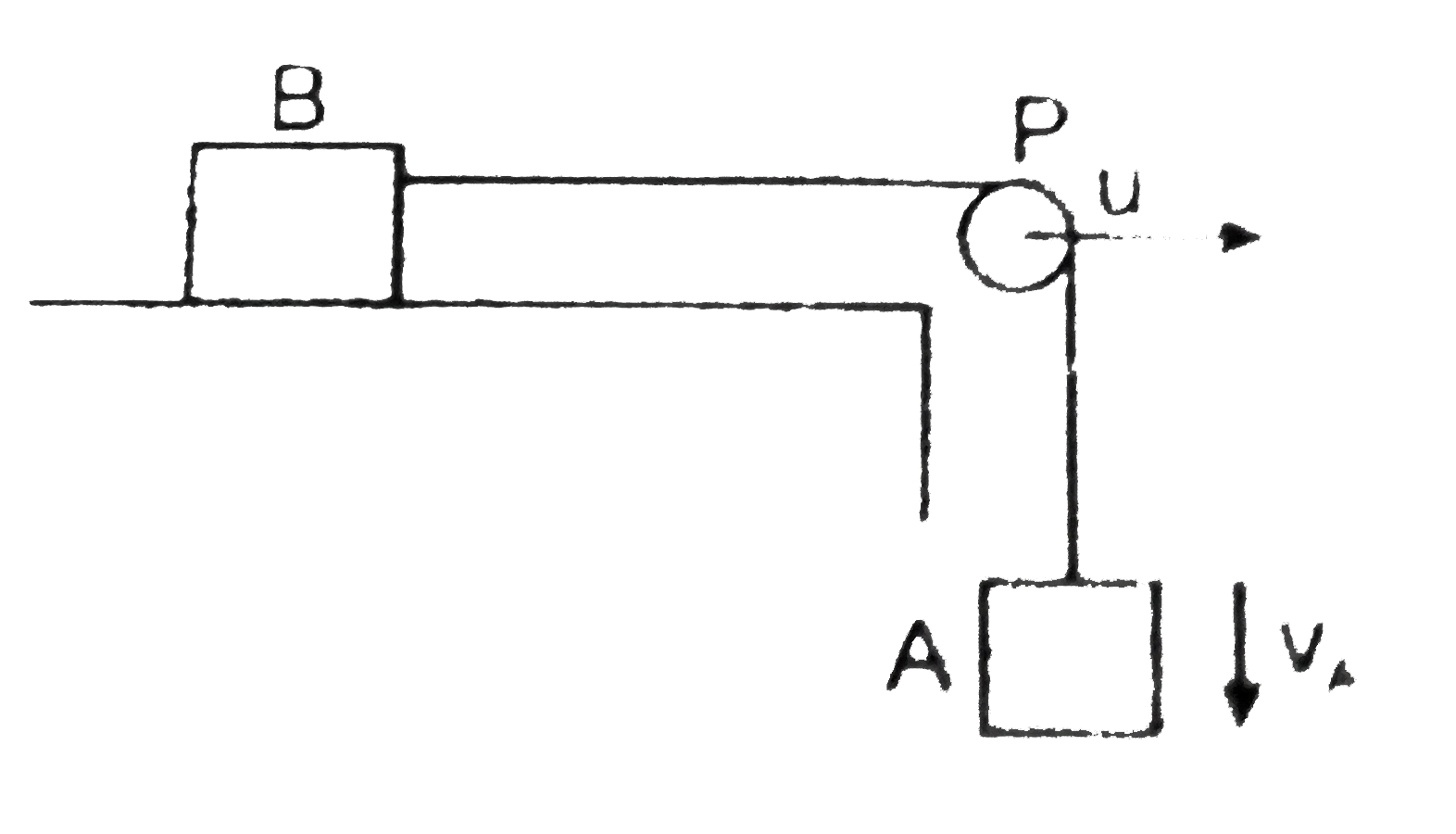
In the figure the pulley P moves to the right with a constant speed u. The downward speed of A is vA and the speed of B to the right VB.
View SolutionIf the blocks A and B are moving towards each other with accelerations a and b shown in fig. find the net acceleration of block C.

View SolutionA rod of length l slided down along the inclined wall as shown in figure. At the instant shown in figure, the speed of end A is v, then the speed of B will be
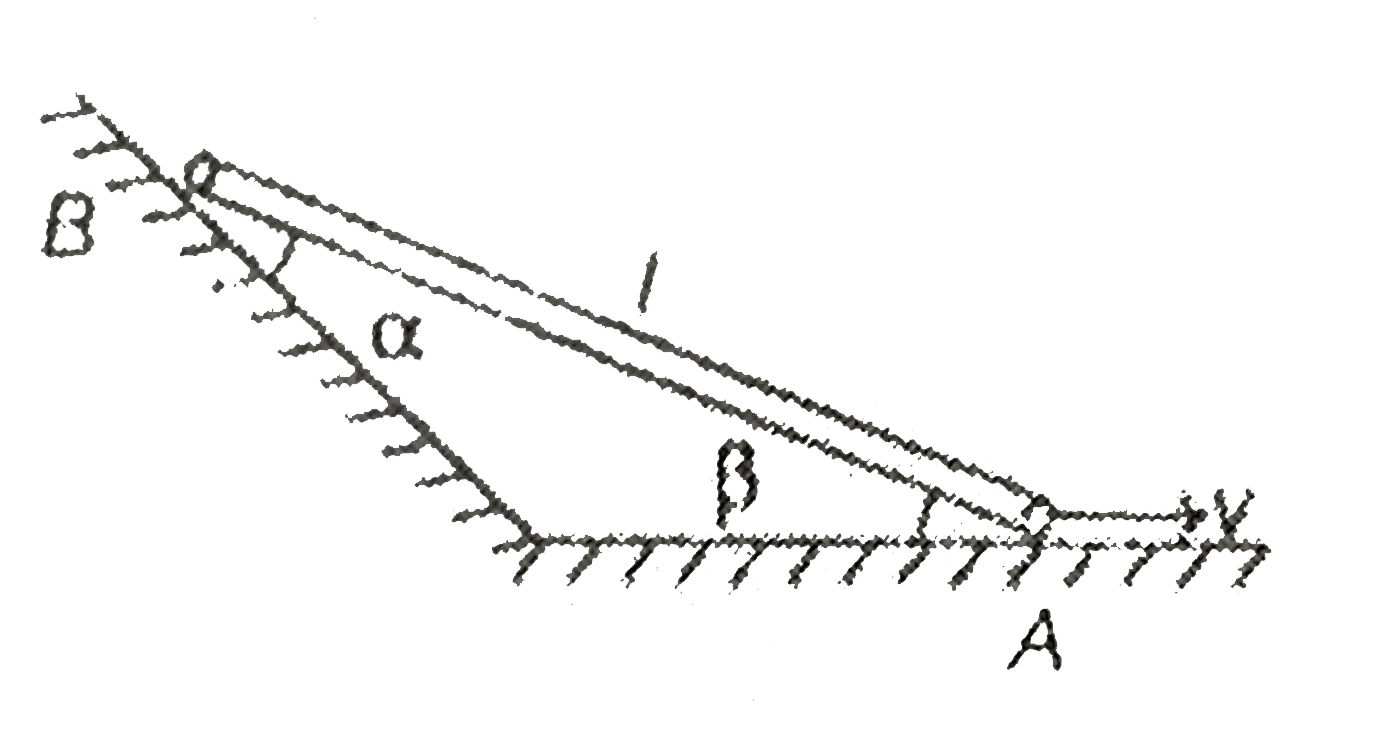
View Solution
