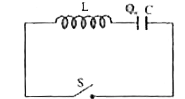
In the following electrical network at $t < 0$ , key is placed on (1) till the capacitor got fully charged. Key is placed on (2) at $t = 0$ . Time when the energy in both the capacitor and inductor will be same for the first time is

Video Solution

Text Solution

Verified by Experts

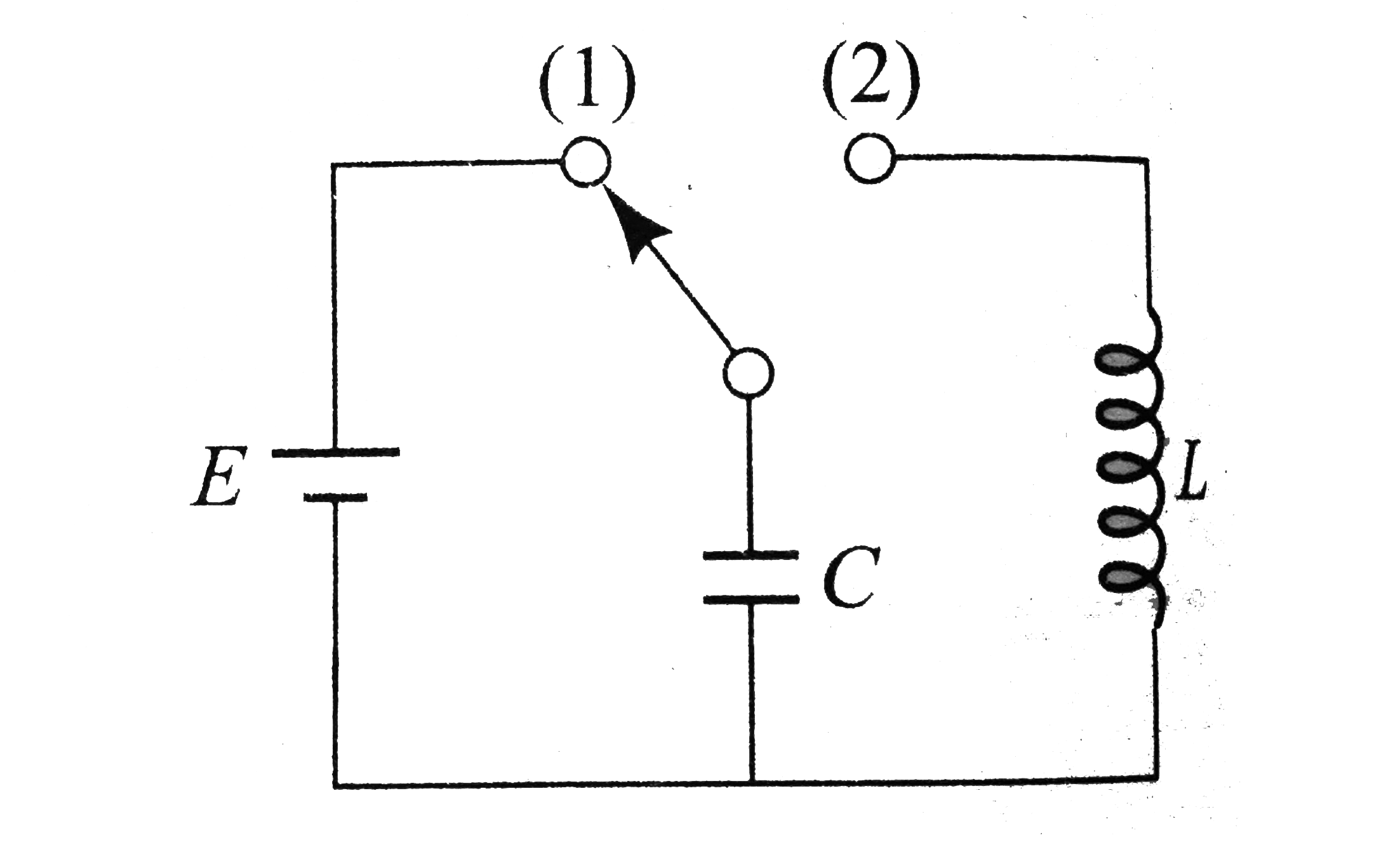
At $t = 0$ , change on capacitor $q_{0} = C E$
Change on capacitor in terms of $t$
$q = q_{0} cos ω t$ , $ω = \frac{1}{\sqrt{L C}}$
$U_{L} + U_{C} = \frac{q_{0}^{2}}{2 C}$
$U_{L} = U_{C}$
$2 U_{C} = \frac{q_{0}^{2}}{2 C}$ implies $U_{C} = \frac{q_{0}^{2}}{4 C}$ implies $\frac{q^{2}}{2 C} = \frac{q_{0}^{2}}{4 C}$
$q = (q_{0}) \frac{'}{\sqrt{2}}$
$q = q_{0} cos ω t$
$\frac{q_{0}}{\sqrt{2}} = q_{0} cos ω t$ implies $cos ω t = \frac{1}{\sqrt{2}} = \frac{cos (π)}{4}$
$ω t = \frac{π}{4}$ implies $t = \frac{π}{4 ω} = \frac{π}{4} \sqrt{L C}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In the following electrical network at $t = < 0$ Fig key is placed on (1) till the capacitor got fully charged. Key is placed on (2) at $t = 0$ . Time when the energy in both the same for the time is

A $\frac{π}{4} \sqrt{L C}$
B $\frac{3 π}{4} \sqrt{L C}$
C $\frac{π}{3} \sqrt{L C}$
D $\frac{2 π}{3} \sqrt{L C}$
Question 2 - Select One or More
In the circuit shown key is closed at $t = 0$ with capacitor initially uncharged.
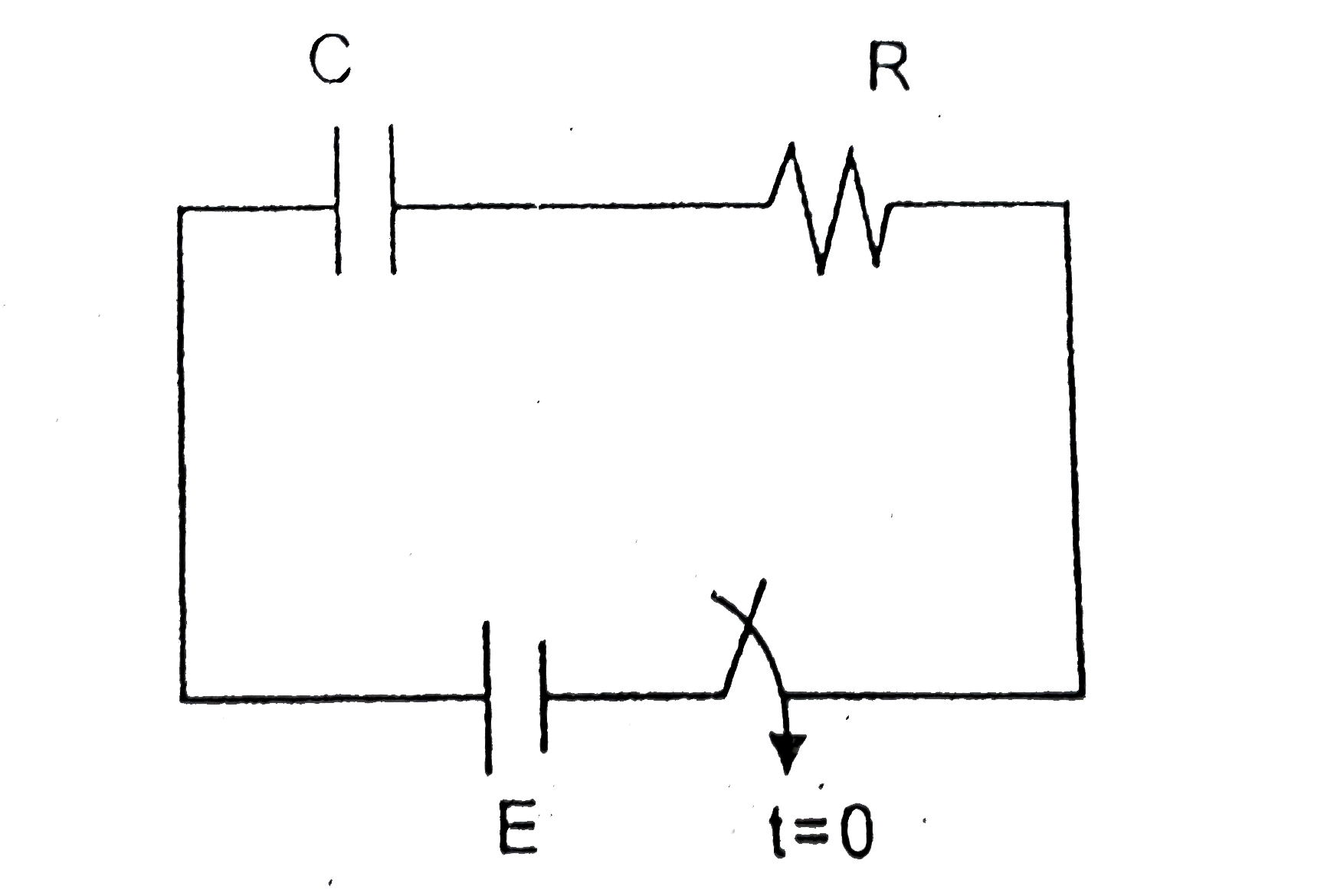ARate of increase of capacitors energy, just after the switch is closed is $\frac{E^{2}}{R}$
BMaximum power supplied by the cell is $\frac{E^{2}}{R}$
CAt $t = R C I n 2$ , capacitor is charged up to half of the energy stored by it in steady state
DAt $t = R C I n 2$ , potential difference across capacitor is same that across resistor.
Question 3 - Select One
The circuit is completed at $t = 0$ , then heat loss in $R = 4 Ω$ resistance, till the capacitor gets fully charged.

A $64 μ J$
B $384 μ J$
C $320 μ J$
D $576 μ J$

CP SINGH-ELECTROMAGNETIC INDUCTION-EXERCISES

Home
Ask Doubt
Profile