A circuit contains 50 μF capacitor and 20 mH inductor connected together with the help of a key which is open initially. Charge stored in the capacitor is 50 mC. Key is closed at t=0 . Calculate the minimum time interval in which energy stored in the inductor becomes equal to the energy stored in capacitor . Neglect any resistance in the circuit .
To solve the problem, we need to determine the minimum time interval in which the energy stored in the inductor becomes equal to the energy stored in the capacitor after the key is closed at t=0.
1. Identify the given values:
- Capacitance C=50μF=50×10−6F
- Inductance L=20mH=20×10−3H
- Initial charge on the capacitor Q=50mC=50×10−3C
2. Calculate the initial energy stored in the capacitor:
The energy stored in a capacitor is given by the formula:
UC=Q22C
Substituting the values:
UC=(50×10−3)22×(50×10−6)=2.5×10−31×10−4=25J
3. Set the energy in the inductor equal to the energy in the capacitor:
The energy stored in the inductor is given by:
UL=12LI2
At the time t when the energies are equal, we have:
UC=UL
Thus,
25=12LI2
4. Express current I in terms of charge q:
The current I can be expressed as:
I=−dqdt
For an LC circuit, the charge q on the capacitor varies with time as:
q(t)=Qcos(ωt)
where ω=1√LC.
5. Calculate ω:
ω=1√LC=1√(20×10−3)(50×10−6)=1√1×10−6=1000rad/s
6. Differentiate q(t) to find I:
I(t)=−dqdt=−ddt(Qcos(ωt))=Qωsin(ωt)
7. Substituting I back into the energy equation:
25=12L(Qωsin(ωt))2
Rearranging gives:
25=12(20×10−3)(50×10−3)2(1000sin(ωt))2
8. Solve for sin(ωt):
Simplifying:
25=0.5×20×10−3×2.5×10−3×106sin2(ωt)
25=25sin2(ωt)
Thus,
sin2(ωt)=1⟹sin(ωt)=1
9. Find ωt:
ωt=π2⟹t=π2ω=π2×1000=π2000≈0.00157s
10. Convert to milliseconds:
t≈1.57ms
Final Answer:
The minimum time interval in which the energy stored in the inductor becomes equal to the energy stored in the capacitor is approximately 1.57 ms.
- Capacitance C=50μF=50×10−6F
- Inductance L=20mH=20×10−3H
- Initial charge on the capacitor Q=50mC=50×10−3C
The energy stored in a capacitor is given by the formula:
UC=Q22C
Substituting the values:
UC=(50×10−3)22×(50×10−6)=2.5×10−31×10−4=25J
The energy stored in the inductor is given by:
UL=12LI2
At the time t when the energies are equal, we have:
UC=UL
Thus,
25=12LI2
The current I can be expressed as:
I=−dqdt
For an LC circuit, the charge q on the capacitor varies with time as:
q(t)=Qcos(ωt)
where ω=1√LC.
ω=1√LC=1√(20×10−3)(50×10−6)=1√1×10−6=1000rad/s
I(t)=−dqdt=−ddt(Qcos(ωt))=Qωsin(ωt)
25=12L(Qωsin(ωt))2
Rearranging gives:
25=12(20×10−3)(50×10−3)2(1000sin(ωt))2
Simplifying:
25=0.5×20×10−3×2.5×10−3×106sin2(ωt)
25=25sin2(ωt)
Thus,
sin2(ωt)=1⟹sin(ωt)=1
ωt=π2⟹t=π2ω=π2×1000=π2000≈0.00157s
t≈1.57ms
The minimum time interval in which the energy stored in the inductor becomes equal to the energy stored in the capacitor is approximately 1.57 ms.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - NCERT FILE (TEXTBOOK EXERCISES )11videos
ALTERNATING CURRENT
- BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - NCERT FILE ADDITIONAL EXERCISES15videos
ALTERNATING CURRENT
- BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - CONCEPTUAL QUESTIONS25videos
ALTERNATING CURRENT
- BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test16videos
ATOMS
Similar Questions
In the steady state of the circuit shown in the figure the ratio of energy stored in the inductor to th energy stored in the capacitor is 10000.
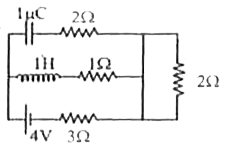 View Solution
View SolutionThe circuit is switched on at t=0, Find the time when energy stored in inductor becomes 1n tiimes of maximum energy stored in it:
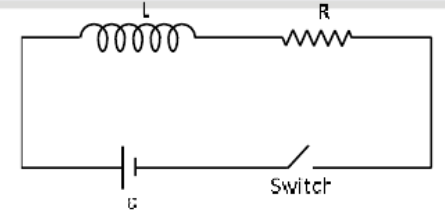 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The capacitor shown in the figure is initially unchanged, the battery is ideal. The switch S is closed at time t= 0, then the time after which the energy stored in the capacitor becomes one - fourth of the energy stored in it in steady - state is :
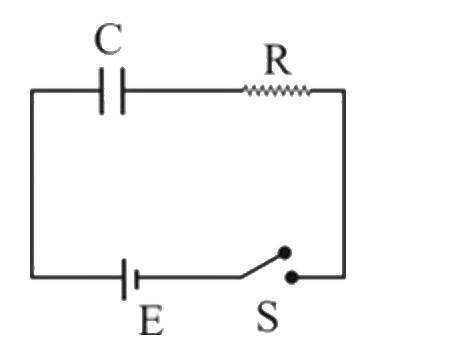 ARCBRC ln 2CRC ln 4D2RC
ARCBRC ln 2CRC ln 4D2RC - Question 2 - Select One
In a decaying L−R circuit, the time after which energy stores in the inductor reduces to one fourth of its initial values is
A(ln2)LRB0.5LRC√2LRD(√2√2−1)LR - Question 3 - Select One
In the circuit what is the change of total electrical energy stored in the capacitors when the key is pressed ?
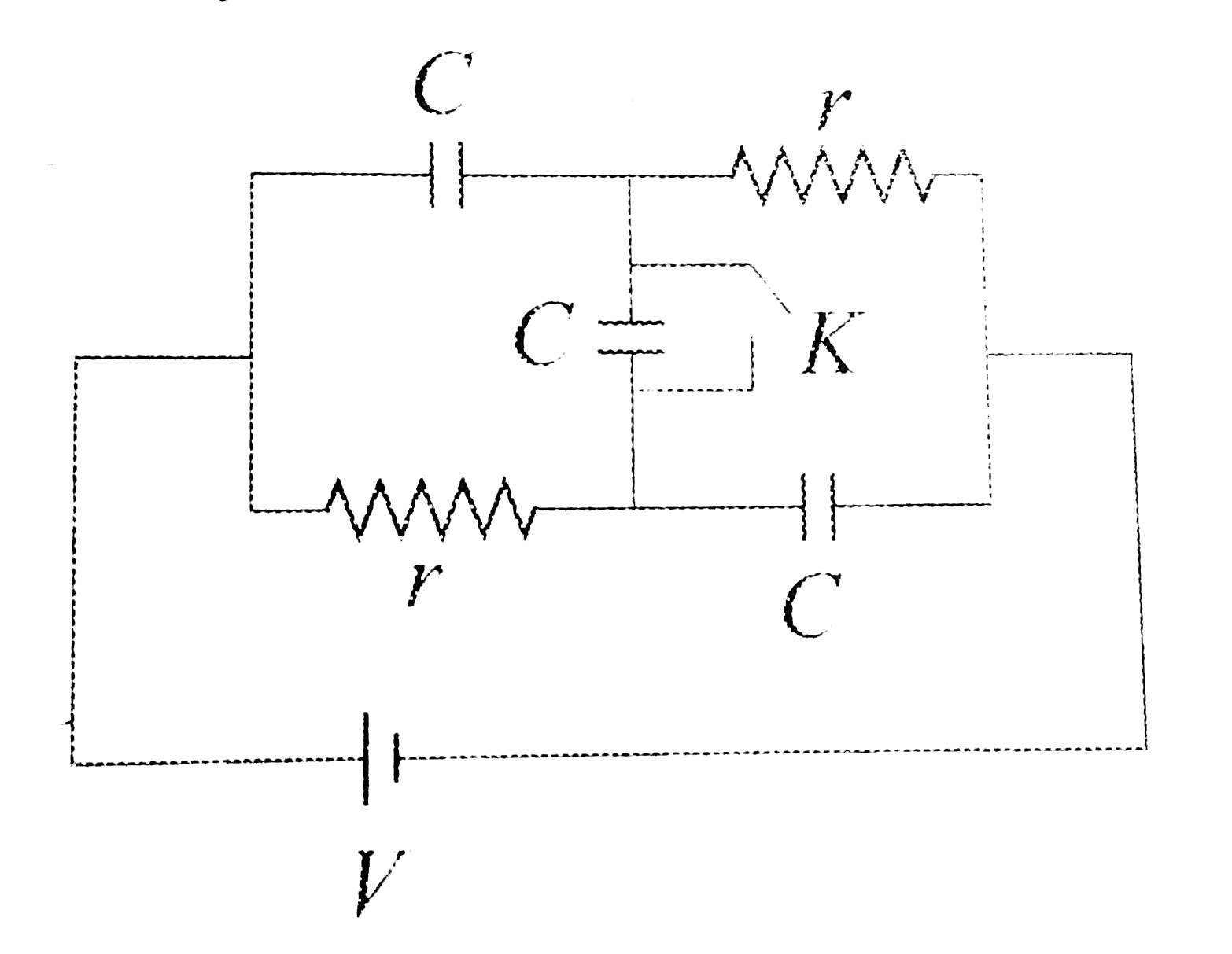 ACV212B7CV28C5CV24D3CV28
ACV212B7CV28C5CV24D3CV28
Figure-5.150 shows LC circuit with initial charge on capacitor 200μC. If at t=0 switch is closed, find the first instant when energy stored in inductor becomes one third that of capacitor.
 View Solution
View Solution
At t=0 switch S is closed .
(a) After how much time , charge on capacitor is 50% of maximum charge stored on capacitor.
(b) After how much time, energy stored in capacitor is halt of maximum energy stored in capacitor.View SolutionA capacitor of capacitance 200μF is connected to a battery through a resistance of 5kΩ at time t = 0. Charge stored in the capacitor in first second in larger than the charge stored in the next
View SolutionA series RLC circuit is connected to an ac generator. The instant at which current in the circuit is zero, the energy stored in the capacitor and inductor are:
View SolutionAn LC circuit contains a 20 mH inductor and 25μF capacitor with an initial charge of 5 mC. The total energy stored in the circuit initially is
View Solution

