In the following figure, a body of mass m is tied at one end of a light string and this string is wrapped around the solid cylinder of mass M and radius R. At the moment t = 0 the system starts moving. If the friction is negligible, angular velocity at time t would be

mgRt(M+m)
2Mgt(M+2m)
2mgtR(M−2m)
2mgtR(M+2m)
The correct Answer is:D
We know the tangential acceleration a=g1+ImR2=g1+1/2MR2mR2=2mg2m+M [As I=12MR2 for cylinder]
After time t, linear velocity of mass m, v=u+at=0+2mgt2m+M
So angular velocity of the cylinder ω=vR=2mgtR(M+2m)
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on centre of mass)
12 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on angular displacement, velocity and acceleration)
16 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple Harmonic Motion
21 Videos
Similar Questions
A light thread with a body of mass m tied to its end is wound on a uniform solid cylinder of mass M and radius R. At a moment t=0 the system is set in motion. Assuming the friction in the axle of the cylinder to be negligible, find the time dependence of
(a) the angular velocity of the cylinder and
(b) the kinetic energy of the whole system ( M=2m).

View SolutionIn the figure, a ball of mass m is tied with two strings of equal as shown. If the rod is rotated with angular velocity ω1 when
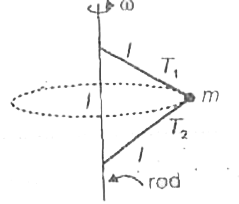
View Solution
Knowledge Check
A body of mass m is tied to free end of dtring and whiled in a circle about the other end .If the string suddenly breaks , then
Acentripetal force will vanishBthe body will move along tangent to circleCthe body will move towards or away the centreDboth 'a' and 'b'A block of mass m is attached to one end of a light string which is wrapped on a disc of mass 2m and radius R. The total length of the slack portion of the string is 1. The block is released from rest. The angular velocity of the disc just after the string becomes taut is
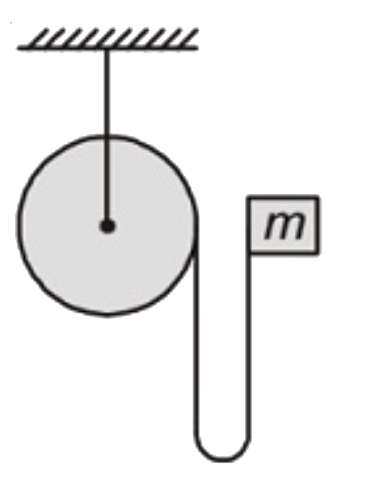 A√glR3B√gl2R2C√2gl3R2D√3gl2R2
A√glR3B√gl2R2C√2gl3R2D√3gl2R2A body of mass 1 kg tied to one end of string is revolved in a horizontal circle of radius 0.1 m with a speed of 3revolution/sec , assuming the effect of gravity is negligible, then linear velocity, acceleration and tension in the string will be
A1.88m/s,35.5m/s2,35.5NB2.88m/s,45.5m/s2,45.5NC3.88m/s,55.5m/s2,55.5NDNone of these
A uniform disc of radius R and mass M is mounted on an axis supported in fixed friction less bearing. A light cord is wrapped around the rim of the wheel and suppose we hang a body of mass m from the cord.
(a) Find the angular acceleration of the disc and tangential acceleration ofpoint on the rim.
(b) At a moment t= 0, the system is set in motion, find the time dependence of the angular velocity of the system and the kinetic energy ofthe whole system.
View SolutionIn the arrangement shown in figure two equal masses (each m) hung light cords wrapped around a uniform solid cylinder of mass M and radius R. The cylinder is free to roate about a harizontal axis. If the system is released from rest then, the tension in each cord is-

View SolutionA mass 'm' is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall or release?
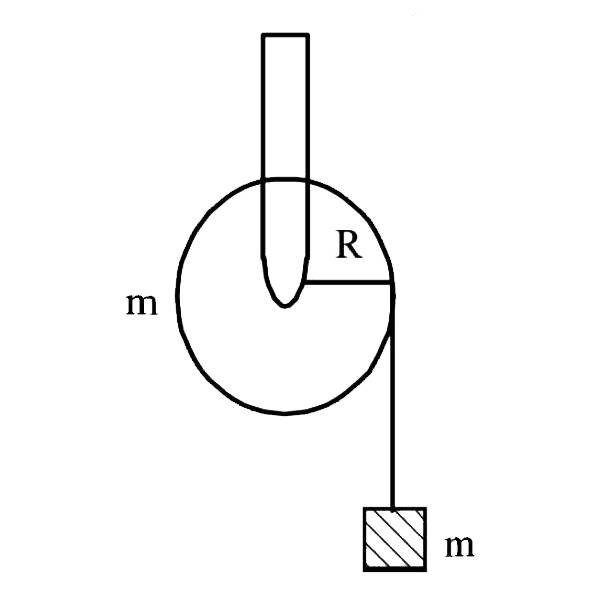
View SolutionA body of mass 100g is tied to one end of a 2m long string. The other end of the string is at the centre of the horizontal circle. The maximum revolution in one minute is 200. The maximum tensible strength of the string is approx
View SolutionA paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are

View Solution
