Question

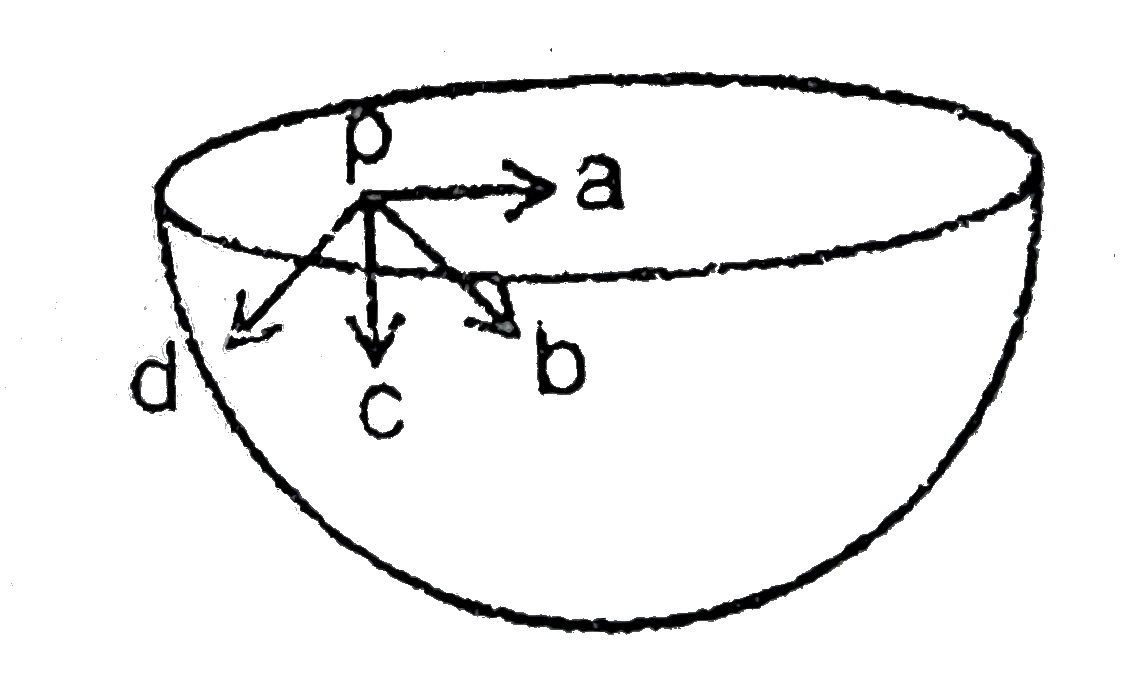
In the following two exercises, choose the correct answer from among the given ones: The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig.) (i) a, (ii) b, (iii) c, (iv) 0.
For the above problem, the direction of the gravitational intensity at an arbitrary point P is indicated by the arrow (i) d, (ii), e, (iii) f (iv) g.

Explanation

At all points inside a hollow spherical shell, potential is same. So, gravitational intensity, which is negative of gravitational potential gradient, is zero. Due to zero gravitational intensity, the gravitational forces acting on any particle at any point inside a spherical shell will be symmetrically placed. It follows from here that if we remove the upper hemispherical shell, the net gravitational force acting on a particle at P will be downwards. Since gravitational intensity is gravitational force per unit mass therefore, the direction of gravitational intensity will be along c. So, option (iii) is correct.