In the given circuit, initially switch S1 is closed, and S2 and S3 are open. After charging of capacitor, at t=0, S1 is opened and S2 and S3 are closed. If the relation between inductance, capacitance and resistance is L=4CR2, tehn find the time (in s) after which current passing through capacitor and inductor will be same (given R=In2mΩ,L=2mH)

The correct Answer is:(1)
After charging, charge on capacitor =Cε
Now, at t=0 two circuits are formed
1. Discharging of capacitor
q=Cεe−t/τC=Cεe−t/RC
i1=−dqdt=ε2Re−t/RC
2. Growth of current in L−R circuit.
i2=ε2R[1−e−t/τL]
Now, i1=i2
(ε).2Re−t/τC=ε2R[1−e−t/τL] ..(i)
Given l=4CR2
L2R=2RC=1In2⇒τC=τL=1In2
Solve to get t=1s
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Archives (fills In The Blanks)
3 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Archives (single Correct )
8 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercises (linked Compreshension)
36 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
28 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
Similar Questions
In given circuit initially switch Sw1 is closed and Sw2 is open, Now Sw1 is opened and Sw2 is closed, what is the heat liberated in resistance R?

View SolutionIn the circult shown
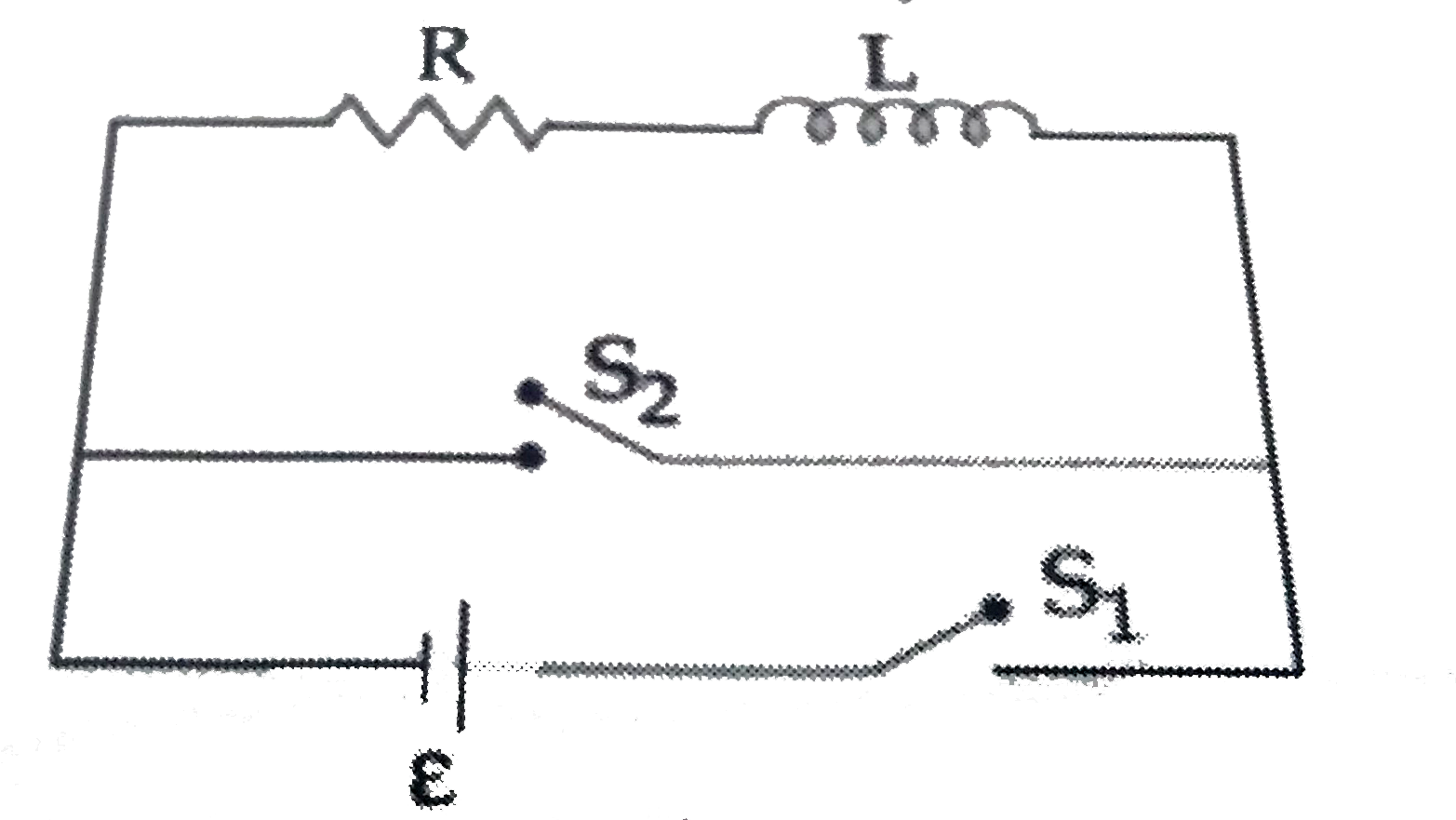 the switch S1 is closed at time t=0 and the swith S2 is kept open. At some later time (t0) ,the swith S1 is opened and S2 is closed .The behaviour of the current I as a function of time 't' is given by :
the switch S1 is closed at time t=0 and the swith S2 is kept open. At some later time (t0) ,the swith S1 is opened and S2 is closed .The behaviour of the current I as a function of time 't' is given by :
View Solution
Knowledge Check
After the capacitor gets fully charged, S1 is opened and S2 is closed so that the inductor is connected in series with the capacitor. Then,
Aat t=0,energy stored in the circuit is purely in the formed of magnetic energy.Bat any time t>0, current in the circuit is in the same directionCat t>0, there is no exchange of energy between the inductor and capacitorDat any timet>0instantaneous current in the circuit mayV√CLIn the circuit shown in the figure, if switches S1 and S2 have been closed for a long time, then charge on the capacitor.
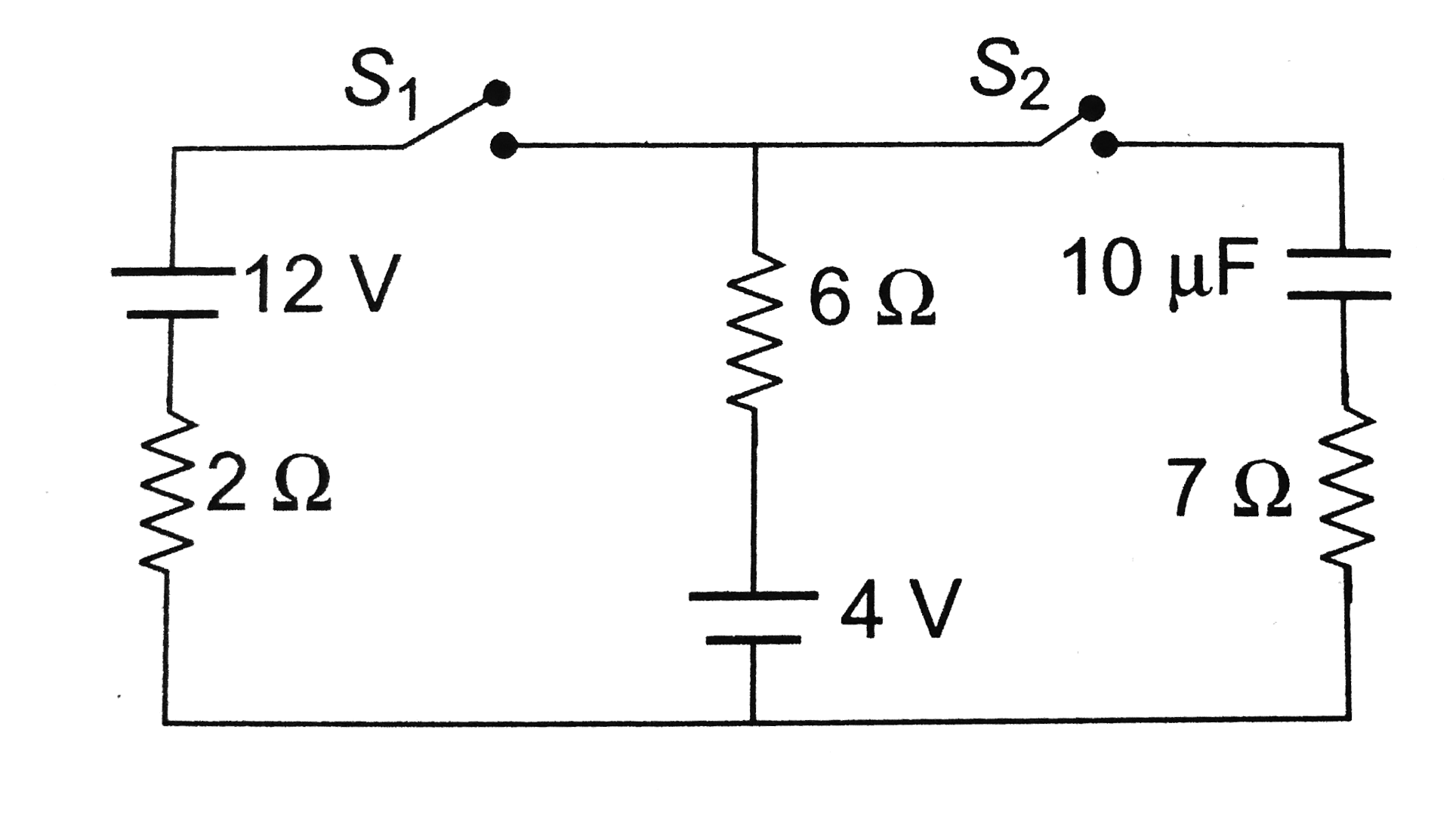 Ais 100μCBincreases to 200μC if one third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same areaCboth (a) and (b) aboveDcharge on the capacitor remains unchanged if one third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same area.
Ais 100μCBincreases to 200μC if one third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same areaCboth (a) and (b) aboveDcharge on the capacitor remains unchanged if one third of the gap of the capacitor's plates is filled with a dielectric (K=2) of same area.In the circuit shows (Fig.) switches S1 and S3 have been closed for 1s and S2 remained open. Just after 1s, switch S2 is closed and S1 and S3 are opened. Find after that instant (t=0):
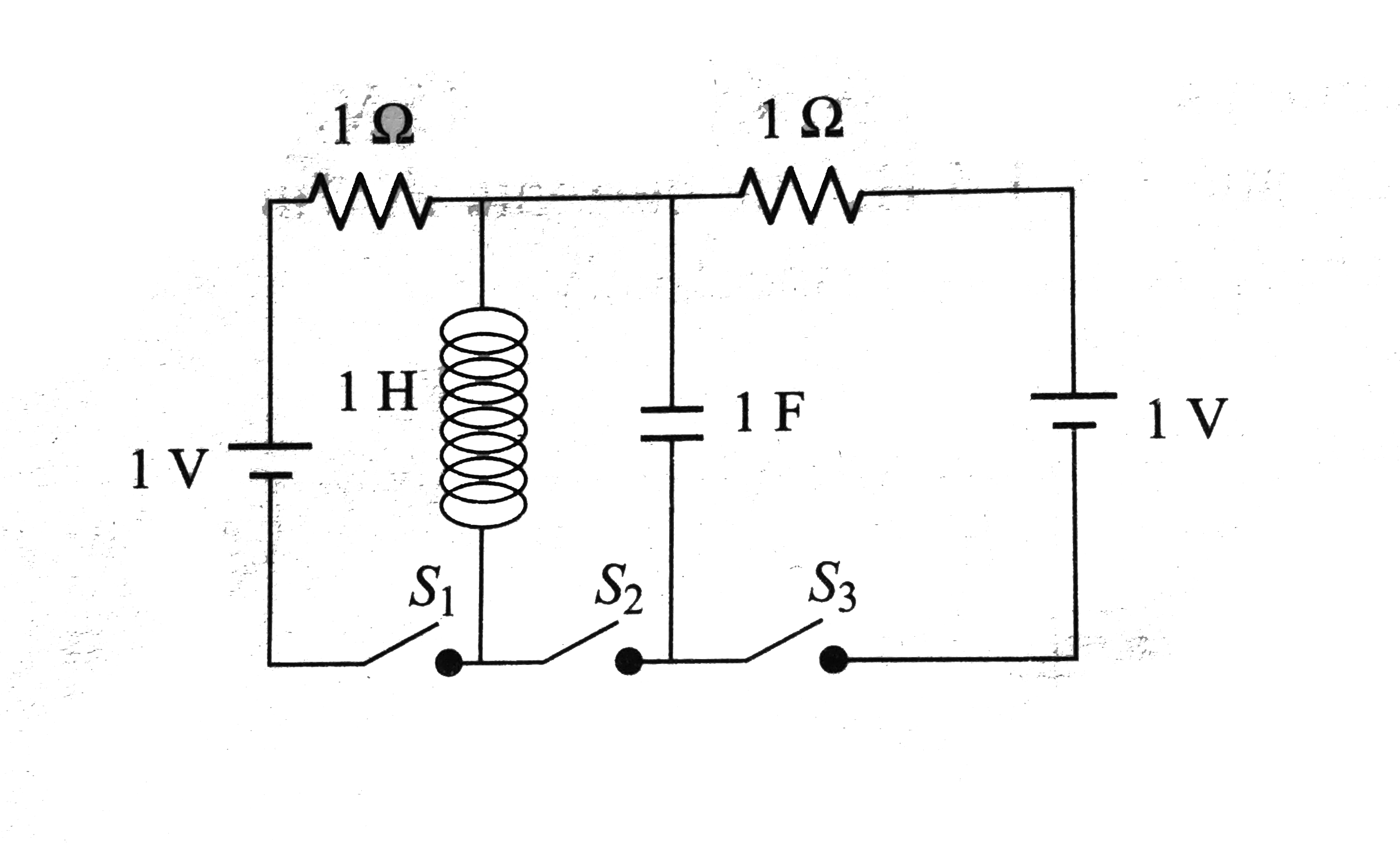
the maximum charge on the capacitorA√3(1+1e)B√3(1−1e)C√2(1+1e)D√2(1−1e)
At any time S1 switch is opened and S2 is closed then find out heat generated in circuit.
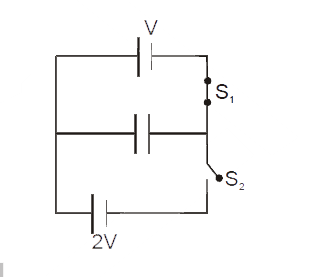
View SolutionIn the given circuit switch S2 is Kept closed and S1 is kept open for a very long time such that the system is in steady- state . Now S1 is also slosed keeping S2 closed.
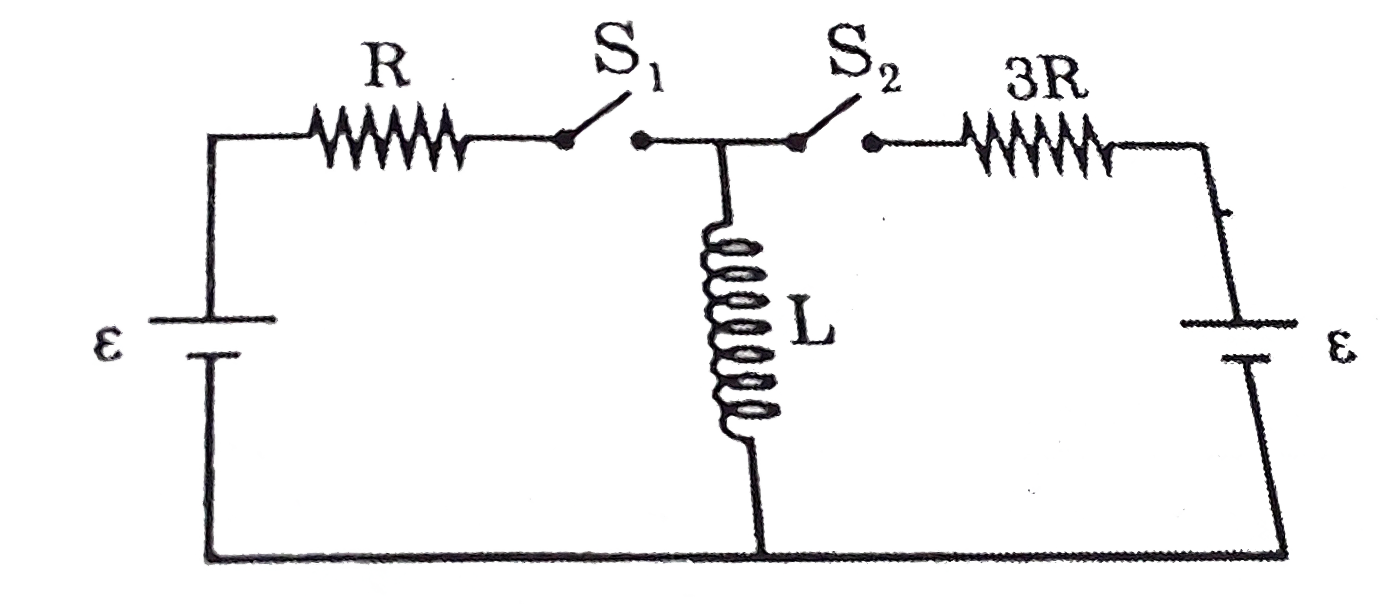
Current passing through inductor L time after S1 is closed , is :
View SolutionIn given circuit initially switch S1 is closed for long time and then opened and now S2 is closed. The total energy dissipated in 4Ω resistor is equal to :-
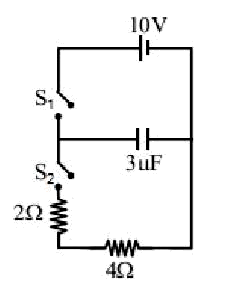
View SolutionInitally switch S1 is closed, after a long time, S1 is opened and S2 is closed. Find the heat produced in coil after long time.
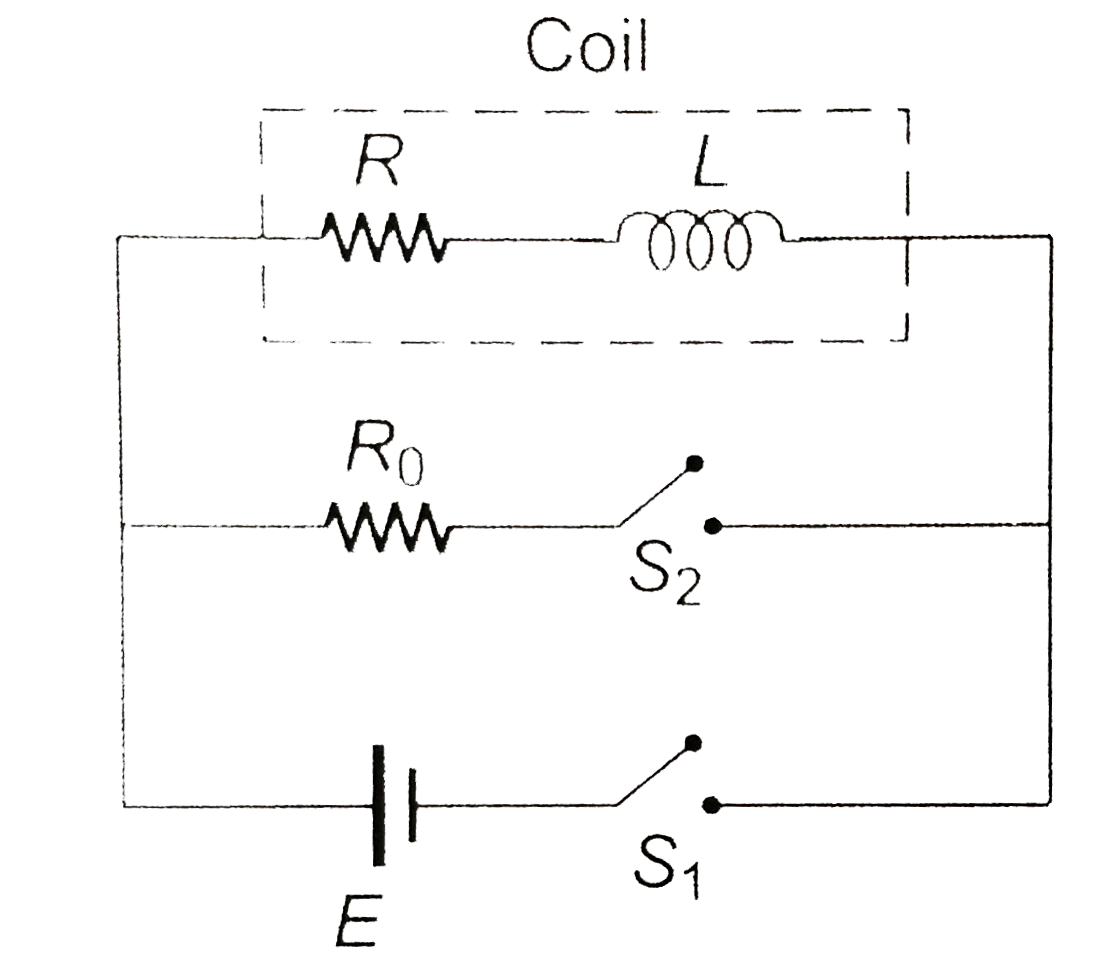
View SolutionIn given circuit all capacitor were uncharged initially. First switch S1 is closed for long time. When circuit reaches to steady state S1 is opened and S2 closed.

The current through R2 jus after closing the switch S2 is
View Solution
