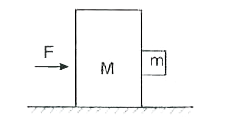
In the given figure, the wedge is acted upon by a constant horizontal force 'F'. The wedge is moving on a smooth horizontal surface. A ball of mass 'm' is at rest relative to the wedge. The ratio of forces exerted on 'm' by the wedge when 'F' is acting and 'F' is withdrawn assuming no friction between the edge and the ball, is equal to :
To solve the problem regarding the wedge and the ball, we will analyze the forces acting on the ball in two scenarios: when the horizontal force F is applied to the wedge and when it is withdrawn. We will then find the ratio of the forces exerted on the ball by the wedge in both cases.
1. Understanding the System:
- We have a wedge on a smooth horizontal surface, and a ball of mass m resting on the wedge.
- The wedge is acted upon by a constant horizontal force F.
2. Forces Acting on the Ball When Force F is Applied:
- When the force F is applied, the wedge accelerates horizontally.
- Let the acceleration of the wedge be aw=FM, where M is the mass of the wedge.
- The ball experiences a normal force N from the wedge and the gravitational force mg acting downward.
- The ball will also have a horizontal pseudo force acting on it due to the acceleration of the wedge, which is maw.
3. Equations of Motion for the Ball:
- The forces acting on the ball can be resolved into components. The normal force N acts perpendicular to the surface of the wedge.
- The vertical component of the normal force balances the weight of the ball:
Ncos(θ)=mg
- The horizontal component of the normal force provides the necessary centripetal force for the ball:
Nsin(θ)=maw
4. Finding the Normal Force N:
- From the first equation, we can express N:
N=mgcos(θ)
- Substituting N into the second equation gives:
mgsin(θ)cos(θ)=maw
- Simplifying this leads to:
gtan(θ)=aw
5. Forces Acting on the Ball When Force F is Withdrawn:
- When the force F is withdrawn, the wedge is no longer accelerating.
- The only forces acting on the ball are its weight mg and the normal force N′ from the wedge.
- In this case, the normal force will only balance the weight of the ball:
N′=mg
6. Ratio of Forces:
- The ratio of the forces exerted on the ball by the wedge when F is acting and when F is withdrawn is given by:
Ratio=NN′=mgcos(θ)mg=1cos(θ)
Final Answer:
The ratio of forces exerted on m by the wedge when F is acting and when F is withdrawn is equal to 1cos(θ).
- We have a wedge on a smooth horizontal surface, and a ball of mass m resting on the wedge.
- The wedge is acted upon by a constant horizontal force F.
- When the force F is applied, the wedge accelerates horizontally.
- Let the acceleration of the wedge be aw=FM, where M is the mass of the wedge.
- The ball experiences a normal force N from the wedge and the gravitational force mg acting downward.
- The ball will also have a horizontal pseudo force acting on it due to the acceleration of the wedge, which is maw.
- The forces acting on the ball can be resolved into components. The normal force N acts perpendicular to the surface of the wedge.
- The vertical component of the normal force balances the weight of the ball:
Ncos(θ)=mg
- The horizontal component of the normal force provides the necessary centripetal force for the ball:
Nsin(θ)=maw
- From the first equation, we can express N:
N=mgcos(θ)
- Substituting N into the second equation gives:
mgsin(θ)cos(θ)=maw
- Simplifying this leads to:
gtan(θ)=aw
- When the force F is withdrawn, the wedge is no longer accelerating.
- The only forces acting on the ball are its weight mg and the normal force N′ from the wedge.
- In this case, the normal force will only balance the weight of the ball:
N′=mg
- The ratio of the forces exerted on the ball by the wedge when F is acting and when F is withdrawn is given by:
Ratio=NN′=mgcos(θ)mg=1cos(θ)
The ratio of forces exerted on m by the wedge when F is acting and when F is withdrawn is equal to 1cos(θ).
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - I
157 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
136 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - Problem
162 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
In the given figure, the wedge is acted upon by a constant horizontal force F. The wedge is moving on a smooth horizontal surface. A ball of mass 'm' is at rest relative to the wedge. The ratio of forces exerted on 'm' by the wedge when F is acting, and when F is withdrawn, assuming no friction between the wedge and the ball, the ratio is equal to

View SolutionA horizontal force F pushes wedge of mass M on a smooth horizontal surface. A block of mass m is stationary to the wedge, then:
View SolutionA block of mass m is at rest on a rough wedge as shown in figure. What is the force exerted by the wedge on the block?

View SolutionA block of mass m is at rest on a rough wedge as shown in figure. What is the force exerted by the wedge on the block?

View SolutionA block of mass m is at rest on a rought wedge as shown in figure. What is the force exerted by the wedge on the block?

View SolutionIn given figure all surfaces are smooth. The ratio of forces exerted by the wedge on mass 'M' when force 'F' is not applied and when 'F' is applied such that 'M' is at rest with respect to wedge is:

View SolutionAll the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :

View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA small ball ( uniform solid sphere ) of mass m is released from the top of a wedge of the same mass m. The wedge is free to move on a smooth horizontal surface. The ball rolld without sliding on the wedge. The required height of the wedge are mentioned in the figure.

The horizontal separation between the ball and the edge 'PQ' of wedge just before the ball falls on the groun is
View Solutiona Block of mass m is placed on a wedge of mass M there is no friction between the block and the wedge .The minmum coefficient of friction between the wedge and the gound so that wedge does not move is,
View Solution
