A block of mass m is placed behind in contact with vertical side of M as shown in the figure. The coefficient of static friction between m and M in μ. The least horizontal force with which m can be pushed so that the two blocks move together is (neglect friction between M and ground).
To solve the problem, we need to determine the least horizontal force F that can be applied to the block of mass m so that both blocks m and M move together without the smaller block sliding down.
1. Identify the Forces Acting on Block m:
- The weight of block m acts downward: Wm=mg.
- The normal force N exerted by block M on block m acts upward.
- The force of static friction fs between the two blocks acts horizontally to the right, opposing the tendency of block m to slide down.
2. Set Up the Vertical Force Balance:
- Since block m is not moving vertically, the normal force N must balance the weight of block m:
N=mg
3. Calculate the Maximum Static Friction:
- The maximum static friction force fs that can act between the two blocks is given by:
fs=μN=μmg
4. Set Up the Horizontal Force Balance:
- When a horizontal force F is applied to block m, both blocks will accelerate together. Let the acceleration of the system be a.
- The friction force must be sufficient to provide the necessary force to accelerate block m:
fs≥ma
- Substituting the expression for static friction:
μmg≥ma
5. Rearranging the Inequality:
- Dividing both sides by m (assuming m≠0):
μg≥a
6. Determine the Least Horizontal Force F:
- The total mass being accelerated is (m+M). The force required to accelerate both blocks together is:
F=(m+M)a
- Since a can be at most μg:
F=(m+M)(μg)
Final Result:
The least horizontal force F with which block m can be pushed so that both blocks move together is:
F=(m+M)μg
- The weight of block m acts downward: Wm=mg.
- The normal force N exerted by block M on block m acts upward.
- The force of static friction fs between the two blocks acts horizontally to the right, opposing the tendency of block m to slide down.
- Since block m is not moving vertically, the normal force N must balance the weight of block m:
N=mg
- The maximum static friction force fs that can act between the two blocks is given by:
fs=μN=μmg
- When a horizontal force F is applied to block m, both blocks will accelerate together. Let the acceleration of the system be a.
- The friction force must be sufficient to provide the necessary force to accelerate block m:
fs≥ma
- Substituting the expression for static friction:
μmg≥ma
- Dividing both sides by m (assuming m≠0):
μg≥a
- The total mass being accelerated is (m+M). The force required to accelerate both blocks together is:
F=(m+M)a
- Since a can be at most μg:
F=(m+M)(μg)
The least horizontal force F with which block m can be pushed so that both blocks move together is:
F=(m+M)μg
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - I157videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II136videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - Problem162videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)10videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)10videos
LOGIC GATES
Similar Questions
A block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it isView SolutionA block of mass m is in contact with the cart C as shown in figure -
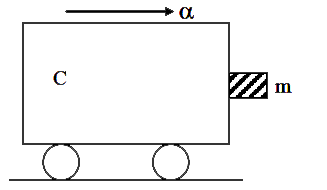
The coefficient of static friction between the block and the cart is μ , The accelertion α of the cart that will prevent the block from failing satisfies -View SolutionA block of mass m is in contact with the cart C as shown in The coefficient of static friction between the block and the cart is μ The acceleration a of the cart that will prevent the block from falling satisfies
 .View Solution
.View SolutionA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?
 View Solution
View SolutionA block of mass M is in contact with a cart of mass M. The coefficient of static friction between block and cart is μ . To prevent the block from sliding on cart, acceleration a should be
View SolutionA block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)
 View Solution
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA wooden block of mass m resting on a rough horizontal table is pulled by a force F as shown in the figure. If μ is the coefficient of friction between block and table, its acceleration will be
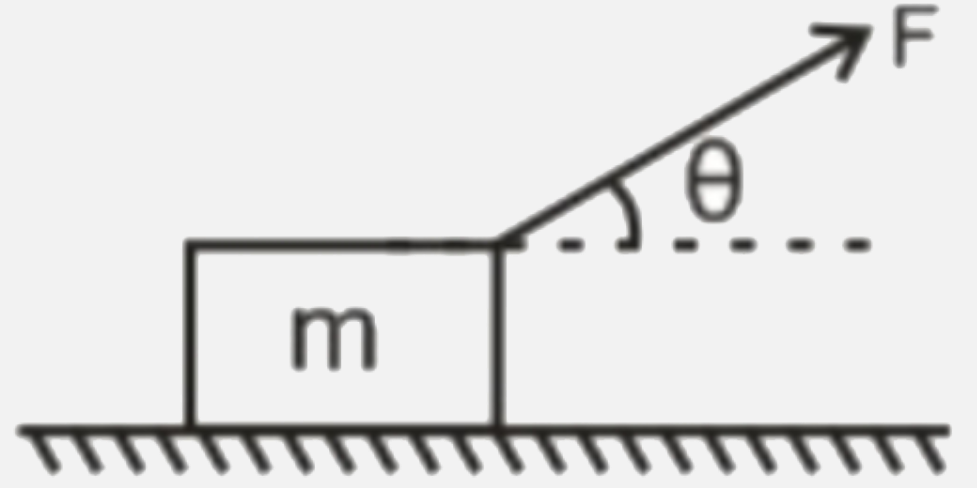 View Solution
View SolutionA block of mass m kg is pushed up against a wall by a force P that makes an angle 'θ' with the horizontal as shown in figure. The coefficient of static friction between the block and the wall is μ. The minimum value of P that allows the block to remain stationary is
View Solution

