A body takes ''n'' times as much time to slide down a rough inclined plane as it takes to slide down an identical but smooth inclined plane. If the angle of inclination of the inclined plane is ''θ''. What is the coefficient of friction between the body and the rough plane ?
To solve the problem, we need to determine the coefficient of friction (μk) between a body and a rough inclined plane, given that the time taken to slide down the rough plane is n times the time taken to slide down an identical smooth inclined plane.
1. Define Variables:
- Let the length of the inclined plane be l.
- The angle of inclination is θ.
- The time taken to slide down the smooth inclined plane is ts.
- The time taken to slide down the rough inclined plane is tr.
2. Time for Smooth Inclined Plane:
- The formula for the time taken to slide down a smooth inclined plane is:
ts=√2lgsinθ
3. Time for Rough Inclined Plane:
- The formula for the time taken to slide down a rough inclined plane, considering friction, is:
tr=√2lg(sinθ−μkcosθ)
4. Relate the Times:
- According to the problem, the time taken on the rough plane is n times that on the smooth plane:
tr=n⋅ts
5. Substituting the Time Formulas:
- Substitute the expressions for tr and ts:
√2lg(sinθ−μkcosθ)=n⋅√2lgsinθ
6. Square Both Sides:
- Squaring both sides to eliminate the square roots:
2lg(sinθ−μkcosθ)=n2⋅2lgsinθ
7. Cancel Out Common Terms:
- Cancel 2l and g from both sides:
1sinθ−μkcosθ=n2⋅1sinθ
8. Cross Multiply:
- Cross multiplying gives:
sinθ=n2(sinθ−μkcosθ)
9. Rearranging the Equation:
- Rearranging the equation leads to:
sinθ=n2sinθ−n2μkcosθ
- Rearranging further gives:
n2μkcosθ=n2sinθ−sinθ
- Factor out sinθ:
n2μkcosθ=(n2−1)sinθ
10. Solving for μk:
- Finally, solve for μk:
μk=(n2−1)sinθn2cosθ
- This can be simplified to:
μk=(n2−1)n2tanθ
Final Result:
The coefficient of friction μk between the body and the rough inclined plane is:
μk=(n2−1)n2tanθ
- Let the length of the inclined plane be l.
- The angle of inclination is θ.
- The time taken to slide down the smooth inclined plane is ts.
- The time taken to slide down the rough inclined plane is tr.
- The formula for the time taken to slide down a smooth inclined plane is:
ts=√2lgsinθ
- The formula for the time taken to slide down a rough inclined plane, considering friction, is:
tr=√2lg(sinθ−μkcosθ)
- According to the problem, the time taken on the rough plane is n times that on the smooth plane:
tr=n⋅ts
- Substitute the expressions for tr and ts:
√2lg(sinθ−μkcosθ)=n⋅√2lgsinθ
- Squaring both sides to eliminate the square roots:
2lg(sinθ−μkcosθ)=n2⋅2lgsinθ
- Cancel 2l and g from both sides:
1sinθ−μkcosθ=n2⋅1sinθ
- Cross multiplying gives:
sinθ=n2(sinθ−μkcosθ)
- Rearranging the equation leads to:
sinθ=n2sinθ−n2μkcosθ
- Rearranging further gives:
n2μkcosθ=n2sinθ−sinθ
- Factor out sinθ:
n2μkcosθ=(n2−1)sinθ
- Finally, solve for μk:
μk=(n2−1)sinθn2cosθ
- This can be simplified to:
μk=(n2−1)n2tanθ
The coefficient of friction μk between the body and the rough inclined plane is:
μk=(n2−1)n2tanθ
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - I157videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II136videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - Problem162videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)10videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)10videos
LOGIC GATES
Similar Questions
A body takes 1(13) times as much time to slide down a rough inclined plane as it takes to slide down an identical bust smooth inclined plane. If the angle of inclination is 45°, find the coefficient of friction.
View SolutionA given object taken n time more time to slide down 45∘ rough inclined plane as it taken to slide down a perfectly smooth 45∘ incline The coefficient of kintic friction between the object and the incline is .
View SolutionAn object takes 1 second to slide down a rough 45∘ inclined plane. The time taken to slide down a smooth 30∘ inclined plane having the same slope length is (μ=0.5)
View SolutionTwo identical blocks A and B of equal masses are placed on rough inclined plane as shown in the figure. Initially the block A is √2m behind the block B. Coefficient of kinetic friction for the blocks A and B are 0.2 and 0.3 respectively (g=10m/s2). By the time the two blocks come on the same line on the inclined plane if they are released simultaneously, the distance moved by B is βm Find the value of β
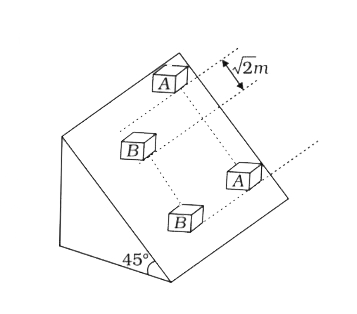 View Solution
View SolutionIn the case of a body sliding down a rough inclined plane show that μs=tanθ
View SolutionA block of mass m slides down a rough inclined plane with an acceleration g2
 View Solution
View SolutionA block of mass m takes time t to slide down on a smooth inclined plane of angle of inclination θ and height h. If same block slids down on a rough inclined plane of same angle of inclination and same height and takes time n times of initial value, then coefficient friction between block and inclined plane is
View SolutionThe time taken by a body to slide down a rough 45∘ inclined plane is twice that required to slide down a smooth 45∘ inclined plane. The coefficient of kinetic friction between the object and rough plane is given by
View SolutionA block slides down on inclined plane (angle of inclination 60∘ ) with an accelration g/2 Find the coefficient friction
 View Solution
View SolutionThe time taken by a block of wood (initially at rest) to slide down a smooth inclined plane 9.8 m long (angle of inclination is 30∘) is
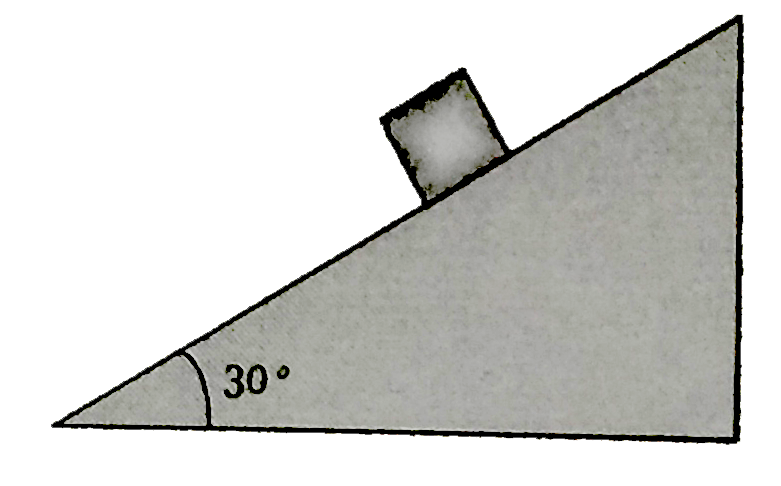 View Solution
View Solution

