In the previous problem what will be refractive index of the liquid so that point E is visible (PE=R/3) through the telescope in air when the vessel is filled with liquid completely, without moving the telesope and vessel.
1.5
√3
√2
none of these
The correct Answer is:d.
Any point ot right of P on surface PA will not be visible when the vessel is filled with liquid.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension51videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective26videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK1videos
FRICTION
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank39videos
GRAVITATION
Similar Questions
A person looking through a telescope T just sees the points on the rim at the bottom of a cylindrical vessel when the vessel is empty. When the vessel is completely filled with a liquid (μ,=1.5), he observes a mark at the centre B,of the bottom without moving the telescope or the vessel. What is the height of the vessel if the diameter of it scross section is 10cm.
View SolutionA person looking through a telescope focuses the lens at a point on the edge of the bottom of an empty cylindrical vessel Next he fills the entire vessel with a liquid of refractive index μ, without disturbing the telescope. Now, he observes the midpoint of the bottom of the vessel Determine the radius to depth ratio of the vessel
View Solution
Knowledge Check
- Question 1 - Select One
In a vessel, as shown in Figure., point P is just visible when no liquid is filled in vessel through a telescope in the air. When liquid is filled in the vessel completely, point Q is visible without movint the vessel or telescope. Find the refractive index of the liquid.
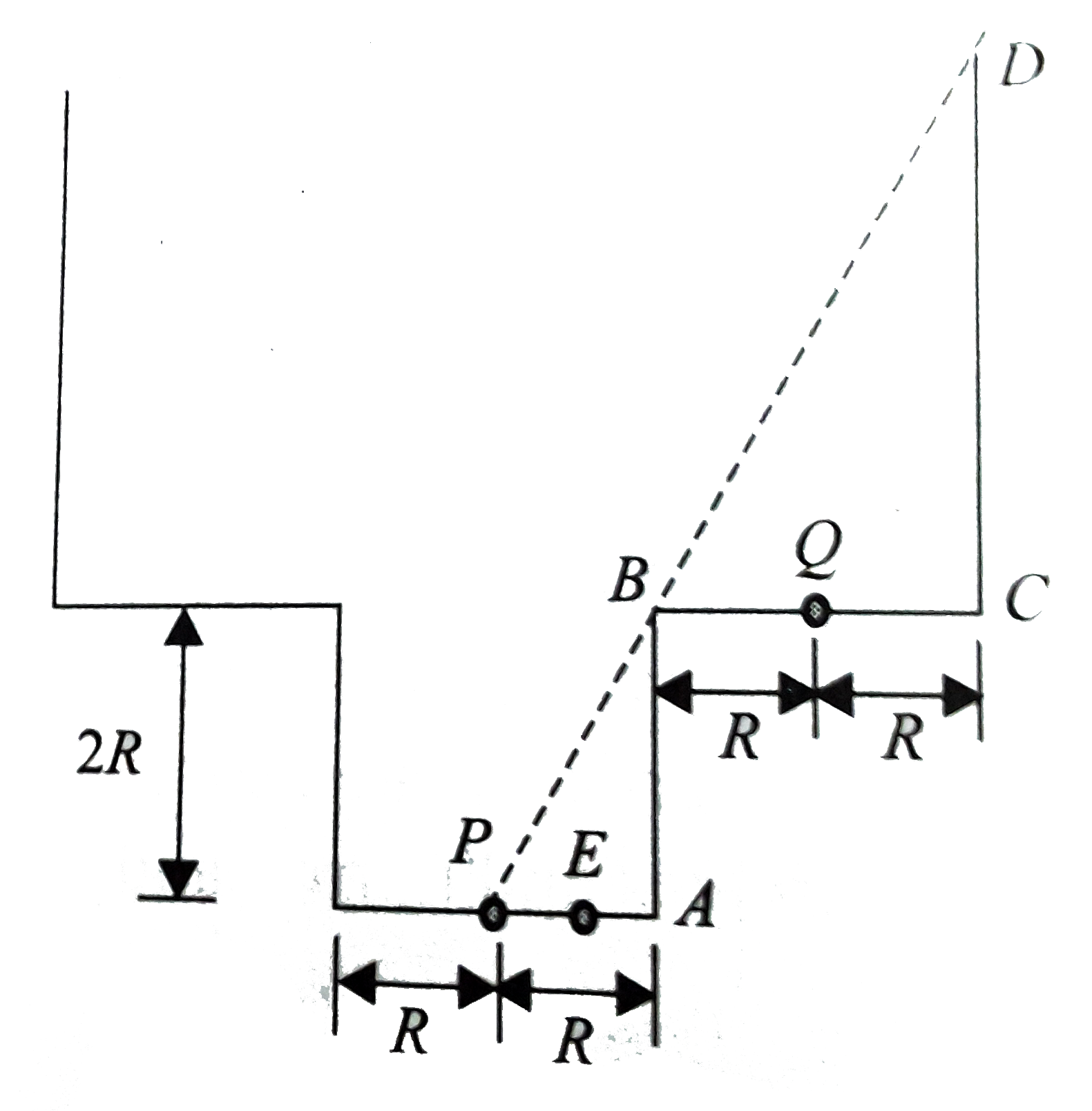 A√143B√855C√2D√3
A√143B√855C√2D√3 - Question 2 - Select One
A vessel of height 2d is half-filled with a liquid of refractive index √2 and the other half with a liquid of refractive index n. (The given liquids are immiscible). Then the apparent depth of the inner surface of the bottom of the vessel (neglecting the thickness of the bottom of the vessel) will be
And(n+√2)Bd(n+√2)n√2Cn√2d(n+√2)Dndd+√2n - Question 3 - Select One
A thin equiconvex lens of refractive index 3/2 is placed on a horizontal plane mirror as shown in figure. The space between the lens and the mirror is filled with a liquid of refractive index 4/3 . It is found that when a point object is placed 15 cm above the lens on its principal axis, the object coincides with its own image.

Q. If another liquid is filled instead of water, the object and the image coincide at a distance 25 cm from the lens.
Calculate the refractive index of the liquid.A1.6B3.2C0.8D2
A cylindrical vessel of radius r containing a liqiud is rotating about a vertical axis through the centre of circular base, If the vessel is rotating with angular velocity ω then what is the difference of the heights of liquid at centre of vessel and edge?
View SolutionA thin equiconvex lens of refractive index 3/2 is placed on a horizontal plane mirror as shown in figure. The space between the lens and the mirror is filled with a liquid of refractive index 4/3 . It is found that when a point object is placed 15 cm above the lens on its priincipal axis, the object coincides with its own image.

Q. If another liquid is filled instead of water, the object and the image coincide at a distance 25 cm from the lens.
Calculate the refractive index of the liquid.View SolutionAn observer can see through a pin-hole the top end of a thin of height h, places as shown in figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
 View Solution
View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
 View Solution
View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The height of beaker is 3h and its radius is h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
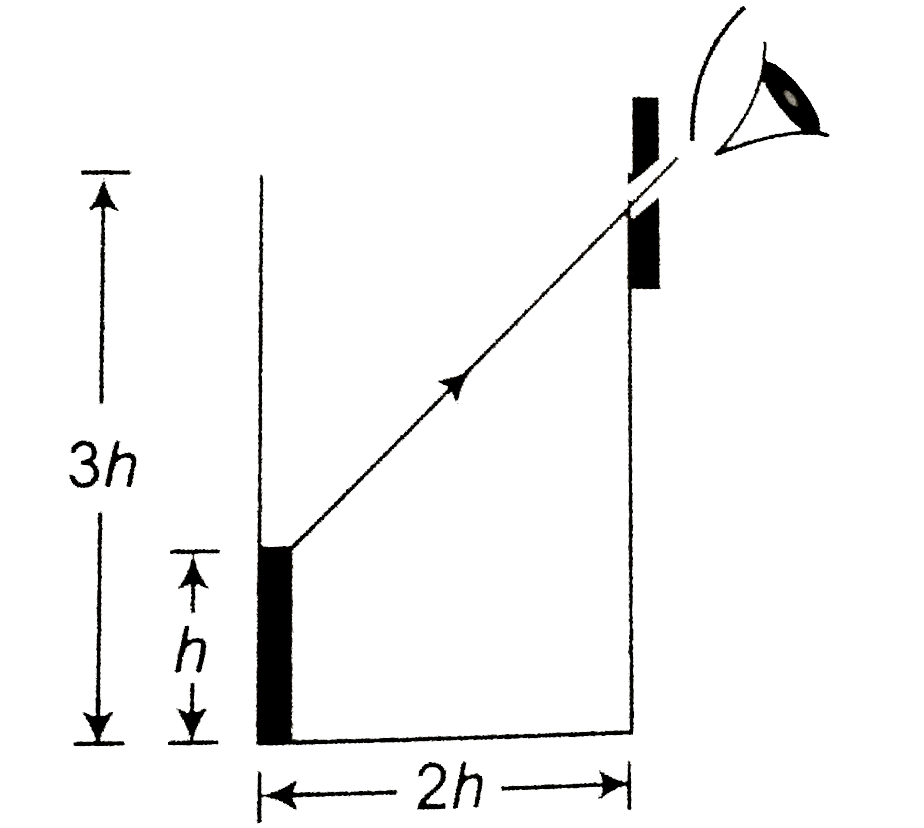 View Solution
View Solution

