In the question number 66, the charge on capacitors C1andC4 are
4×10−3C,12×10−3C
6×10−3C,12×10−3C
2×10−3C,4×10−3C
3×10−3C,2×10−3C
The correct Answer is:A
To solve the problem regarding the charge on capacitors C1 and C4, we can follow these steps:
Step 1: Understand the Configuration
We need to determine the charge on capacitors C1 and C4. From the previous question, we know that the charge on capacitors C1,C2, and C3 is the same, denoted as Q, while the charge on capacitor C4 is denoted as Q′.
Step 2: Write the Equation for Total Charge
The total charge in the circuit can be expressed as:
QC1+QC2+QC3=600
This implies that:
Q(1C1+1C2+1C3)=600
Step 3: Find the Equivalent Capacitance
The term 1C1+1C2+1C3 represents the equivalent capacitance Cs of the series combination of C1,C2, and C3. Therefore, we can write:
Q=600×Cs
Step 4: Calculate the Charge Q
Assuming Cs is given as 203μF:
Q=600×203μC=4000μC=4×10−3C
Step 5: Find the Charge Q′ on Capacitor C4
For capacitor C4, we can express the charge as:
Q′C4=600
This leads to:
Q′=C4×600
Step 6: Substitute the Value of C4
Assuming C4=200μF:
Q′=200×600μC=120000μC=12×10−3C
Final Answers
- Charge on capacitor C1: Q=4×10−3C
- Charge on capacitor C4: Q′=12×10−3C
We need to determine the charge on capacitors C1 and C4. From the previous question, we know that the charge on capacitors C1,C2, and C3 is the same, denoted as Q, while the charge on capacitor C4 is denoted as Q′.
The total charge in the circuit can be expressed as:
QC1+QC2+QC3=600
This implies that:
Q(1C1+1C2+1C3)=600
The term 1C1+1C2+1C3 represents the equivalent capacitance Cs of the series combination of C1,C2, and C3. Therefore, we can write:
Q=600×Cs
Assuming Cs is given as 203μF:
Q=600×203μC=4000μC=4×10−3C
For capacitor C4, we can express the charge as:
Q′C4=600
This leads to:
Q′=C4×600
Assuming C4=200μF:
Q′=200×600μC=120000μC=12×10−3C
- Charge on capacitor C1: Q=4×10−3C
- Charge on capacitor C4: Q′=12×10−3C
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - HOTS5videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXEMPLAR PROBLEMS3videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason15videos
ELECTROMAGNETIC WAVES
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar5videos
MAGNETISM AND MATTER
Similar Questions
Condsider
.
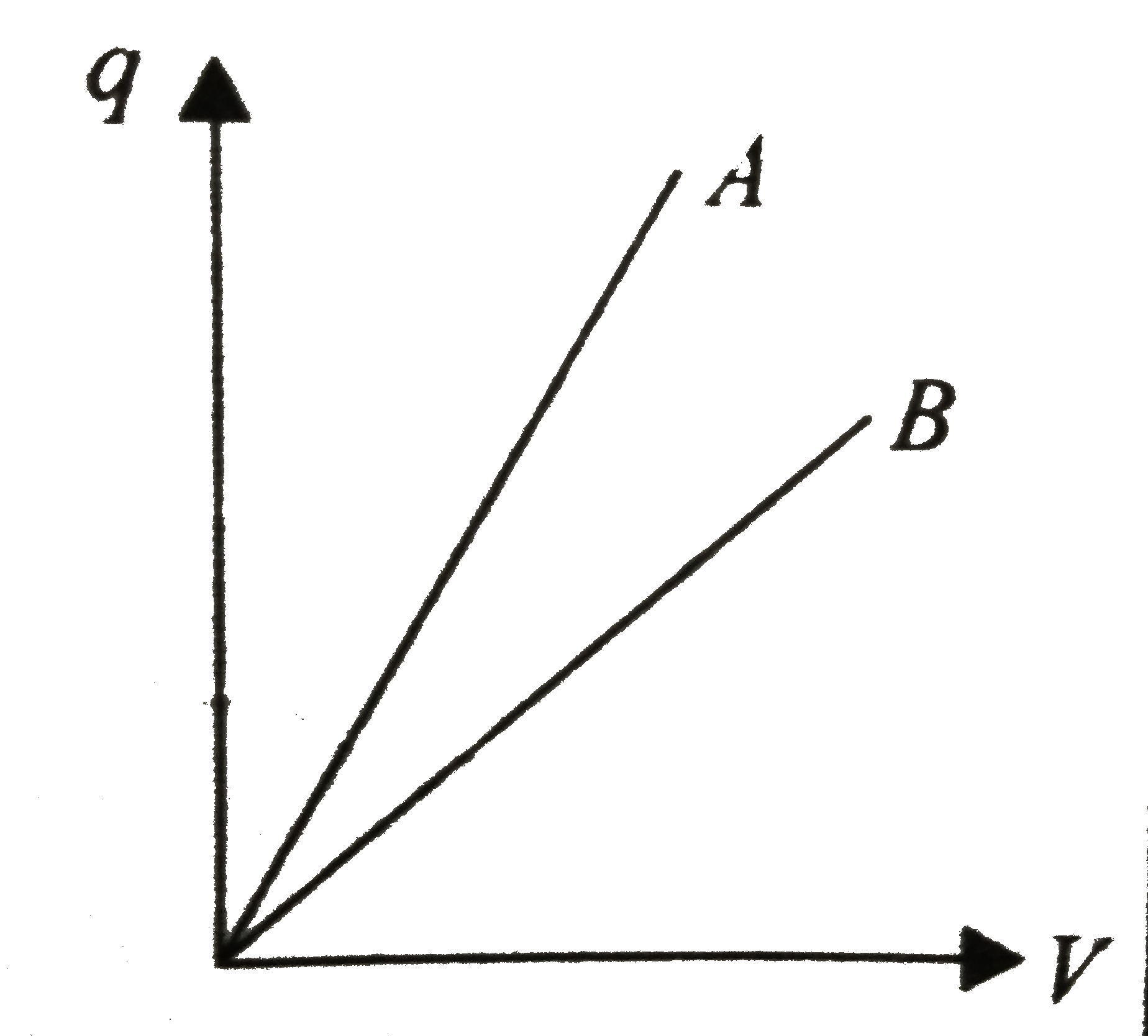
The charge on capacitor C1 is.View SolutionShows these variation of charge q for two capacitors C1 and C2 The two capacitors have the same plate separation. But the plate area of C2 is double than that of C1. Which of the lines in the figure corresponds to C1 and C2 and why?
.View Solution
Knowledge Check
- Question 1 - Select One
In the question number 66, the tension in the string is
A30NB36NC34ND32N - Question 2 - Select One
In the circuit given, the charge on capacitor C3 at steady state is
A6μCB12μCC18μCD24μC
The circuit shown in fig 5.223 is in steady state.
find the charges on the capacitors C1andC2 respectively.
View SolutionThree capacitors are connected as shwn in. Then, the charge on capacitor C1 is .
. View Solution
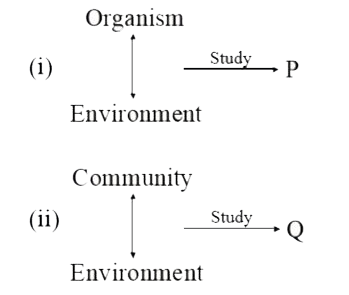
then P and Q are respectively called as.View SolutionTwo capacitors of equal capacitance (C1=C2) are as shown in the figure. Initially, while the swithc is open (as shown) one of the capacitors is uncharged and the other carries charge Q0. The energy stored in the charged capacitor is U0. Sometime after the switch is closed, the capacitors C1andC2 carry charged Q1andQ2 respectively, the energy stored in the capacitors are U1andU2 respectively. Which of the following expression is correct?
View SolutionTwo capacitors C1 and C2 are charged 2uF AND 3uF seperately to potentials 20Vand10V, respectively. The terminals of capacitors C1andC2 are marked as (A-B) and (C-D), respectvely. A is connected with CandB is connected with D.
i. Find the final potential dsifference across each eapacitors.
ii. Find the final charge in both capacitors
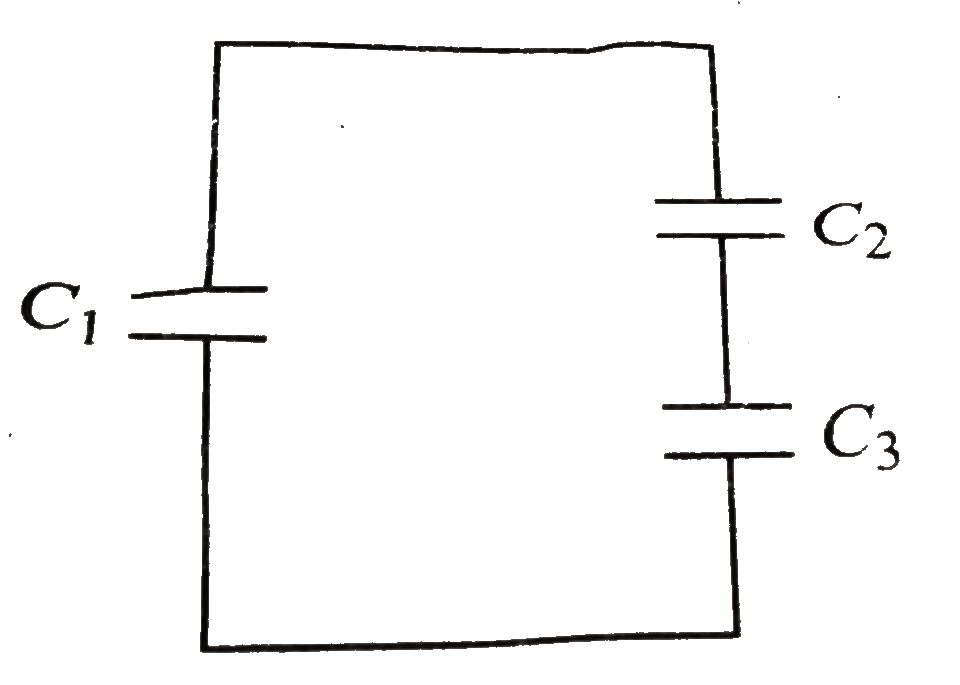
iii. How much heat is produced in the circuit.View SolutionCapacitor C1 is connected to a battery and charged till the magnitude of the charge on each plate is q0. Then, the battery is disconnected and C1 is connected to two other uncharged capacitors C2andC3 as shown in figure. Final charges on the capacitors (q1,q2andq3) are related by .
View Solution