In the question number 73, for the coil given the magnetic moment is
12.95Am2
25.79Am2
10.05Am2
24.79Am2
The correct Answer is:C
To find the magnetic moment of a circular coil, we can use the formula:
Magnetic Moment(M)=n⋅I⋅A
Where:
- n = number of turns in the coil
- I = current flowing through the coil
- A = area of the coil
1. Identify the given values:
- Number of turns, n=100
- Current, I=3.2A
- Radius of the coil, R=10cm=0.1m (conversion from cm to m)
2. Calculate the area of the circular coil:
The area A of a circle is given by the formula:
A=πR2
Substituting the value of R:
A=π(0.1)2=π⋅0.01m2
Using π≈3.14:
A≈3.14⋅0.01=0.0314m2
3. Substitute the values into the magnetic moment formula:
M=n⋅I⋅A
M=100⋅3.2⋅0.0314
4. Perform the multiplication:
First, calculate 100⋅3.2=320:
M=320⋅0.0314
Now, multiply:
M≈10.048A m2
5. Round the result:
Rounding to two decimal places, we get:
M≈10.05A m2
Final Answer:
The magnetic moment of the coil is approximately 10.05A m2.
- n = number of turns in the coil
- I = current flowing through the coil
- A = area of the coil
- Number of turns, n=100
- Current, I=3.2A
- Radius of the coil, R=10cm=0.1m (conversion from cm to m)
The area A of a circle is given by the formula:
A=πR2
Substituting the value of R:
A=π(0.1)2=π⋅0.01m2
Using π≈3.14:
A≈3.14⋅0.01=0.0314m2
M=n⋅I⋅A
M=100⋅3.2⋅0.0314
First, calculate 100⋅3.2=320:
M=320⋅0.0314
Now, multiply:
M≈10.048A m2
Rounding to two decimal places, we get:
M≈10.05A m2
The magnetic moment of the coil is approximately 10.05A m2.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - HOTS5videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXEMPLAR PROBLEMS6videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar5videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
Similar Questions
A 100 turn closely wound circular coil of radius 10cm carries a current of 3⋅2A. (i) What is the field at the centre of the coil? (ii) What is the magnetic moment of this arrangement?
View SolutionWith reference to magnetic dipole, match the tems of Column I with the tems of Column Ii and Choose the correct option from the codes given below.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the question number 73, the given coil is placed in a vertical plane and is free to rotate about a horizontal axis which coincides with its diameter. A uniform magnetic field of 5T in the horizontal direction exists such that initially the axis of the coil is in direction of the field. The coil rotates through an angle of 60∘ under the influence of magnetic field. The magnitude of torque on the coil in the final position is
A25 N mB25√3NmC40 N mD40√3Nm
A uniform conducting wire of length length 10a and resistance R is wound up into four turn as a current carrying coil in the shape of equilateral triangle of side a. If current I is flowing 4 through the coil then the magnetic moment of the coil is
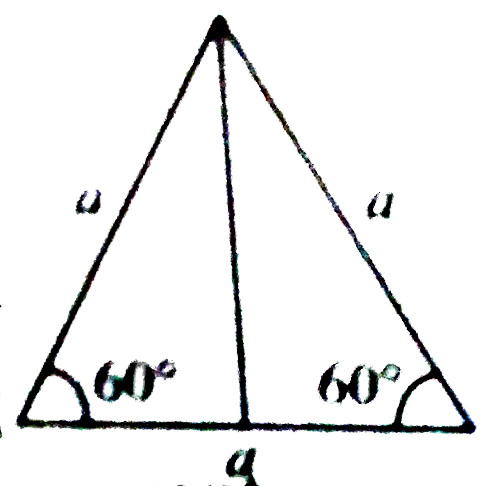 View Solution
View SolutionWhen equal current is passed through two coils equal magnetic field is produced at their centers. If the ratio of number of turns in the coils is 8:15 then the ratio of the their radii will be
View SolutionYou are given two coils A and B. Through each coil, the initial magnetic flux is same. In which coil, the em.f. induced will be more if the number of turns in the coil A is twice that of the coil B and the magnetic flux is reduced to zero in coil A, two times faster than in coil B?
View SolutionA circular coil of closely wound N terns and radius r carriers a current I.
Write the expressions for the following :
(i) the magnetic field at its centre
(ii) the magnetic moment of this coilView SolutionA wire of length 2 m carrying a current of 1 A is bend to form a circle. The magnetic moment of the coil is (in Am2)
View SolutionA regular hexagone of side a. A wire of length 24 a is coiled on that hexagone. If current in hexagone is I, then find the magnetic moment.
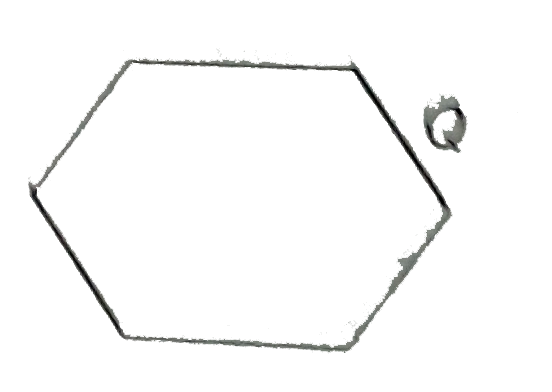 View Solution
View SolutionObtain the formula I=Kθ for a moving coil galvanometer, given the deflecting torque →τ=→m×→B where m is the magnetic dipole moment of the coil placed in the magnetic field B, I is the current in the galvanometer and θ is the direction.
View Solution

