In the ray diagram shown here, calculate the speed of light in the liquid of unknown refractive index.
To calculate the speed of light in the liquid of unknown refractive index, we will follow these steps:
Step 1: Understand the relationship between refractive index and critical angle
The refractive index n of a medium can be related to the critical angle C using the formula:
sinC=1n
This means that if we know the critical angle, we can find the refractive index.
Step 2: Calculate sinC
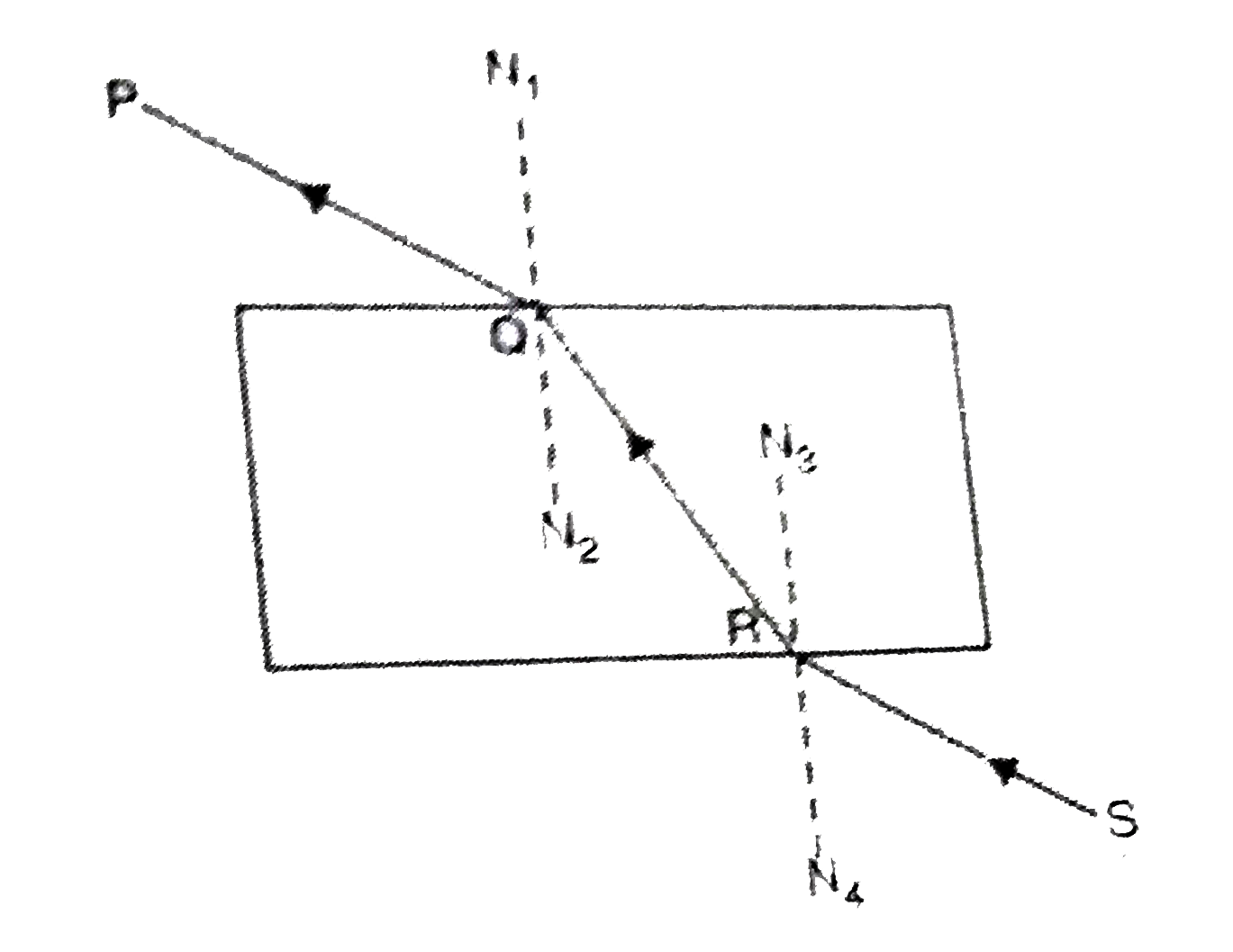
From the problem, we know that the critical angle C is given. We can express sinC in terms of the sides of a right triangle formed in the ray diagram. If we assume the opposite side (perpendicular) to be 30 and the adjacent side (base) to be 40, we can find the hypotenuse using the Pythagorean theorem:
Hypotenuse=√302+402=√900+1600=√2500=50
Thus,
sinC=OppositeHypotenuse=3050=35
Step 3: Find the refractive index n
Using the relationship from Step 1:
sinC=1n⟹n=1sinC=135=53
Step 4: Calculate the speed of light in the medium
The speed of light in a medium can be calculated using the formula:
V=Cn
Where C is the speed of light in vacuum (approximately 3×108 m/s). Substituting the values we have:
V=3×108 m/s53=3×108×35=9×1085=1.8×108 m/s
Final Answer
The speed of light in the liquid of unknown refractive index is:
1.8×108 m/s
---
The refractive index n of a medium can be related to the critical angle C using the formula:
sinC=1n
This means that if we know the critical angle, we can find the refractive index.
From the problem, we know that the critical angle C is given. We can express sinC in terms of the sides of a right triangle formed in the ray diagram. If we assume the opposite side (perpendicular) to be 30 and the adjacent side (base) to be 40, we can find the hypotenuse using the Pythagorean theorem:
Hypotenuse=√302+402=√900+1600=√2500=50
Thus,
sinC=OppositeHypotenuse=3050=35
Using the relationship from Step 1:
sinC=1n⟹n=1sinC=135=53
The speed of light in a medium can be calculated using the formula:
V=Cn
Where C is the speed of light in vacuum (approximately 3×108 m/s). Substituting the values we have:
V=3×108 m/s53=3×108×35=9×1085=1.8×108 m/s
The speed of light in the liquid of unknown refractive index is:
1.8×108 m/s
Topper's Solved these Questions
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Sample problem(c)
3 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Sample problem(d)
5 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions
7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assertion- Reason Type questions
20 Videos
Similar Questions
(i) Define refractive index of a medium.
(ii) In the following ray diagram, calculate the speed of light in the liquid of unknown refractive index.
View SolutionHow is the refractive index of a medium related to the speed of light? Obtain an expression for refractive index of a medium with respect to another in terms of speed of light in these two media?
View Solution
Knowledge Check
The speed of light in a medium of refractive index 1.5 is ________.
A1.5×108m/sB3.0×108m/sC2.0×108m/sD1.2×108m/sIn the figure shown, the angle made by the light ray with the normal in the medium of refractive index √2 is
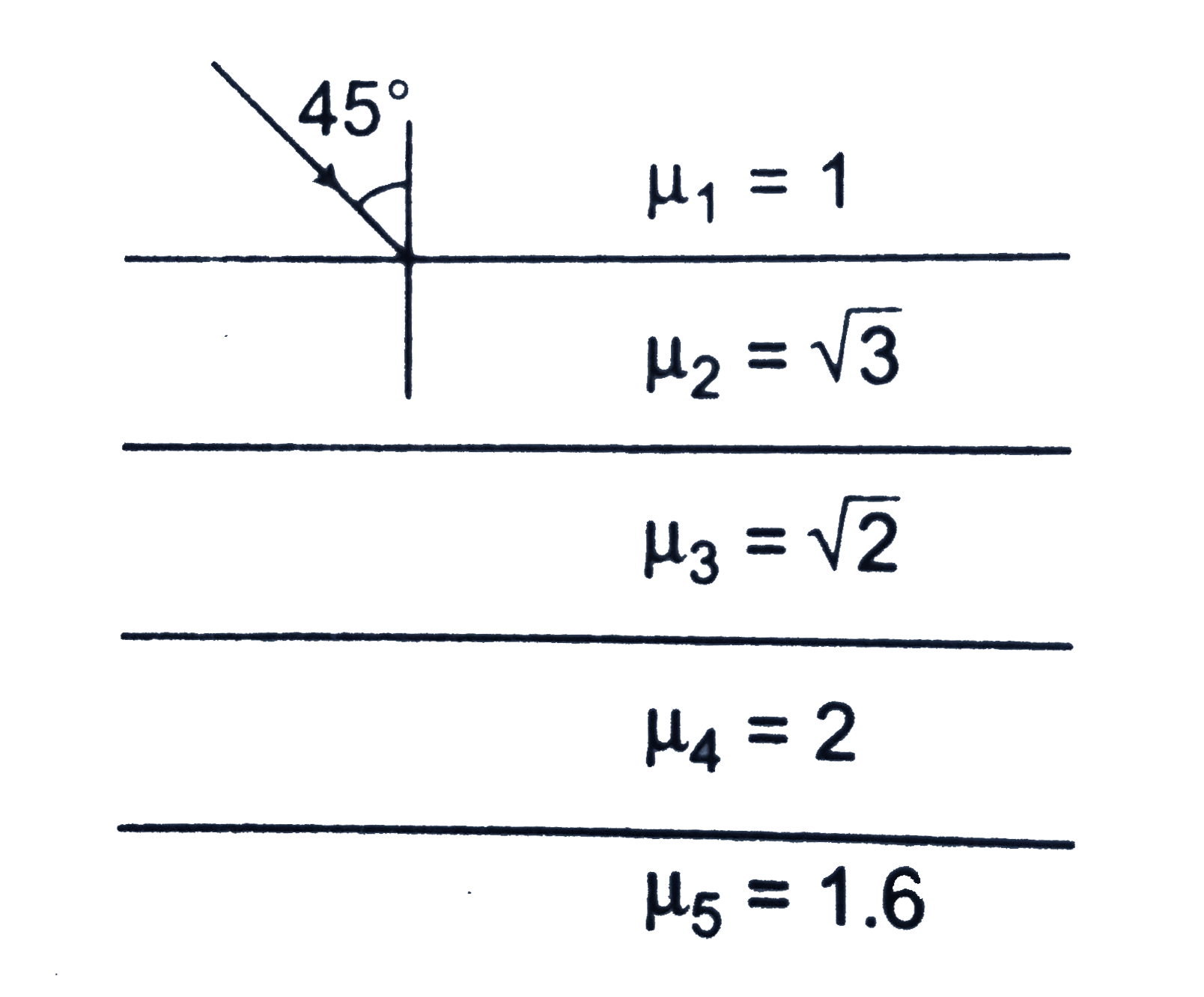 A30∘B60∘C90∘DNone of these
A30∘B60∘C90∘DNone of theseThe table below gives the refractive index of a few materials and the speed of light in that medium
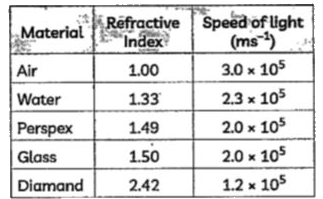
The speed of light in a medium 'A' having refractive index 2 .00 will beA1.5×108m/sB2.0×108m/sC3.0×108m/sD6.0×108m/s
How is the refractive index of a medium related to the speed of light ? Obtain an expression for refractive index of a medium with respect to another in terms of speed of light in these two media ?
View SolutionCalculate the angle of emergence (e) of the ray of light incident normally on the face AC of a glass prism ABC of refractive index √3. How will the angle of emergence change qualitatively, if the ray of light emerges from the prism into a liquid of refractive index 1.3 instead of air ?
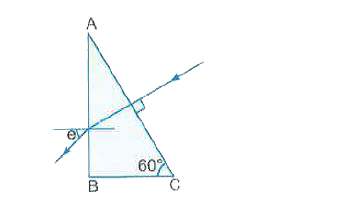
View Solution(a) Draw the ray diagram showing refraction of ray of light through a glass prism. Derive the expression for the refractive index n of the material of prism in terms of the angle A ray angle of minimum deviation δm
(b) A ray of light PQ enters an isosceles right angles prism ABC of refractive index 1.5 as shown in figure .
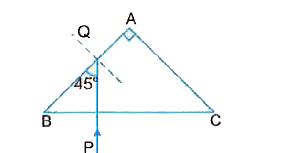
(i) Trace the path of the ray through the prism .
(ii) What will be the effect on the path of the ray if refractive index of the prism is 1.4 ?
View SolutionWhen the rectangular metal tank is filled to the top with an unknown liquid, as observer with eyes level with the top of the tank can just see the corner E , a ray that refracts towards the observer at the top surface of the liquid is shown. The refractive index of the liquid will be

View SolutionAn experiment for tracing the path of a ray of light through a glass slab was set up in the laboratory and ray diagram was drawn as shown here.
The teacher asked the students to identify the refracted ray. The correct answer is :
View Solution
