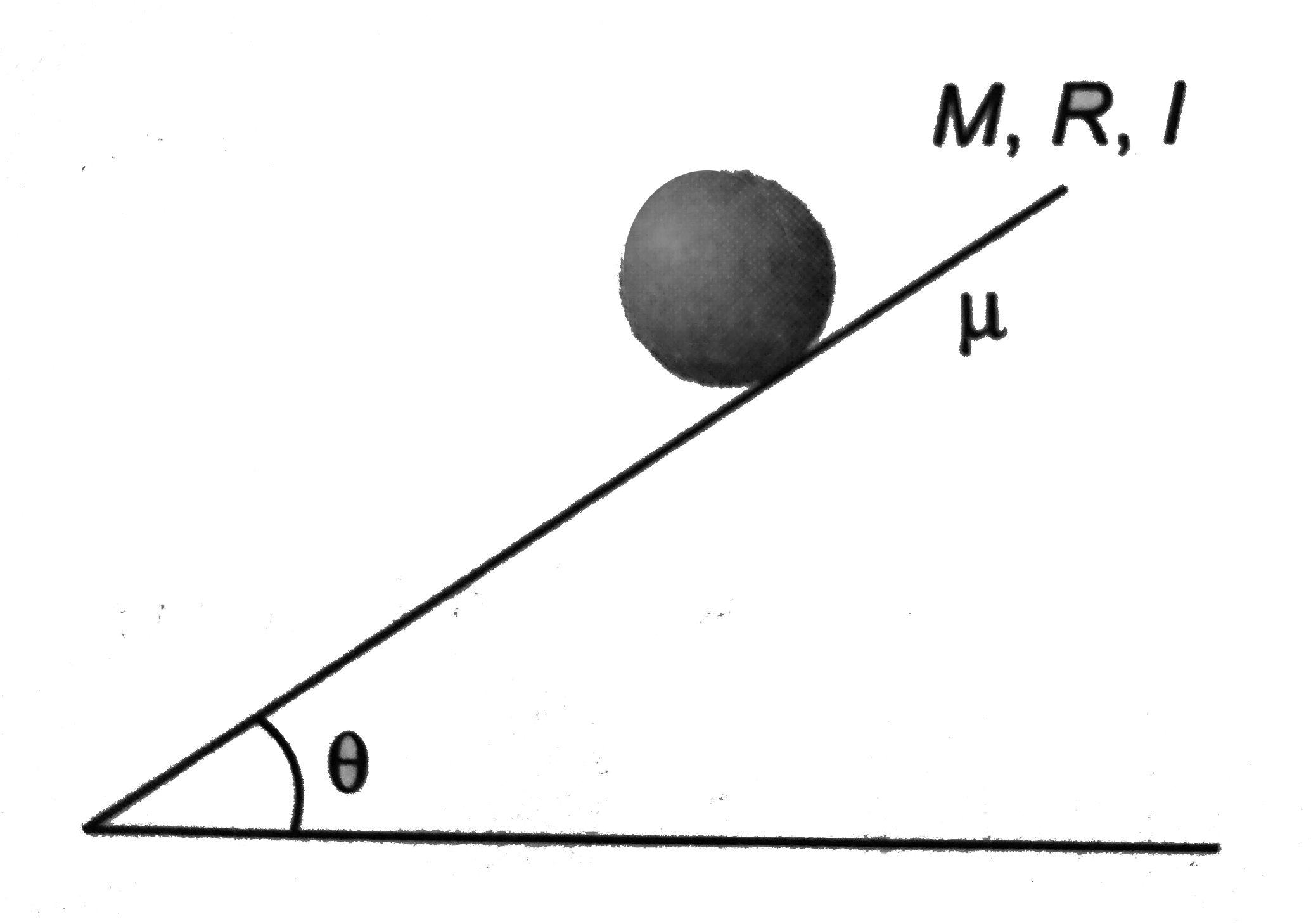
In the shown figure, M is mass of the body, R its radius an I the moment of inertial about an axis passing through centre. Find force of friction f acting on the body (upwards), its linear acceleration a (down the plane) and type of motion if:
(a) μ=0
(b). μ<μmin
(c). μ>μmin
Where μmin is the minimum value of coefficient of friction required for pure rolling
(a). If μ=0 then
f=0 and a=gsinθ=a1 (say)
and the motion is only translational.
(b). If μ<μmin then maximum value of friction will act. As friction is insufficient to provide acclerated pure rolling or to stop the relative motion. ltbr> ∴f=fmax=μmgcosθ
and a=Mgsinθ−μMgcosθm
=gsinθ−μgcosθ=a2 (say)
In this case, motion is rotation + translatio with forward slip (as a>Rα)
(c). if μ>μmin, then we have discussed in the above article that
f=Mgsinθ1+MR2I⎞⎟⎠ and a=gsinθ1+IMR2=a3 (say)
Motion i this case is rotation + translation with accelerated pure rolling.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Examples
25 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
Knowledge Check
For the same total mass which of the following will have the largest moment of inertia about an axis passing through its centre of mass and perpendicular to the plane of the body.
Aa disc of radius aBa ring of radius oaCa square lamina of side 2aDfour rods forming a square of side 2a.Find the moment of inortia of ring of mass m and radius R about an axis passing through its centre and making an angle of 45∘ with its plane:
 AMR24BMR22C34MR2DMR2
AMR24BMR22C34MR2DMR2Moment of inertia of a rigid body about an axis passing through its centre of mass is I0 and moment of inertia of the same body about another axis parallel to the first axis is I. Then
AI is always equal to I0BI is always smaller than I0CI is always greater than I0Dany of the above three
A thin semi circular cylindrical shell has mass M and radius R. Find its moment of inertia about a line passing through its centre of mass parallel to the axis (shown in figure) of the cylinder.

View Solution
A body of mass m, radius R and moment of inertia I (about an axis passing through the centre of mass and perpendicular to plane of motion) is released from rest over a sufficiently rough ground (to provide accelerated pure rolling) find linear acceleration of the body.
View SolutionCalculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionA rigid body of mass m rotates about an axis passing through its centre. If the angular velocity of the body is unity, the moment of inertia of the body will be equal to
View SolutionA rigid body of mass m rotates about an axis passing through its centre. If the angular velocity of the body is unity, the moment of inertia of the body will be equal to
View Solution

