In the situration shown in the figure the friction coefficient between M and the horizontal surface is μ. The force F is applied at an angle θ with vertical. The correct statements are
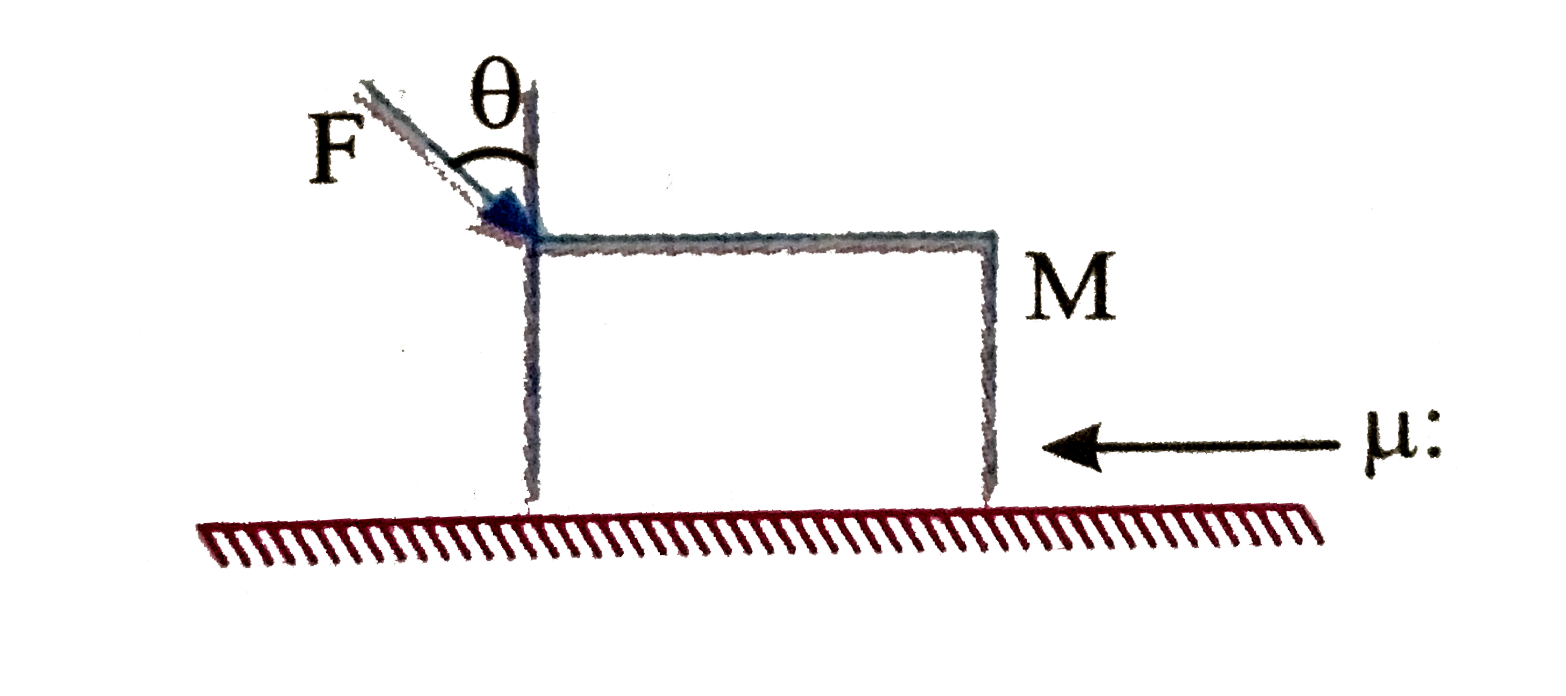
If θ>tan−1μ the block cannot be pushed forward for any value of F
If θ<tan−1μ the block cannot be pushed forward for any value of F
As θ decreases the magnitude of force needed to just push the block M forward increases .
none of the above
The correct Answer is:A, C

N = F cos θ+Mg …..(i)
fmax=μ(M−2m)3 ….(ii)
To just push the block F sin θ=fmax
⇒Fsinθμ(Fcosθ+Mg)
⇒F=μMgsinθ−μcosθ
⇒sinθ−μcosθ>0⇒tanθ>μ
⇒tanθ>tan(tan−1μ)⇒θ>tan−1μ
Hence , the block can be pushed forward only if θ>tan−1μ
Again as θ decreases sin θ decreases while cos θ increases , therefore , sin θ−μcosθ decreases . Hence , μMgsinθ−μcosθ increases .
Topper's Solved these Questions
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Assertion - Reason
12 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Matrix - Match
5 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - OBJECTIVE QUESTIONS ( only one choice is correct )
80 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Comprehension type Queston
14 Videos
Similar Questions
The friction coefficient between the blocks is μ. If force F is applied on the lower block , analyse motion of two blocks.

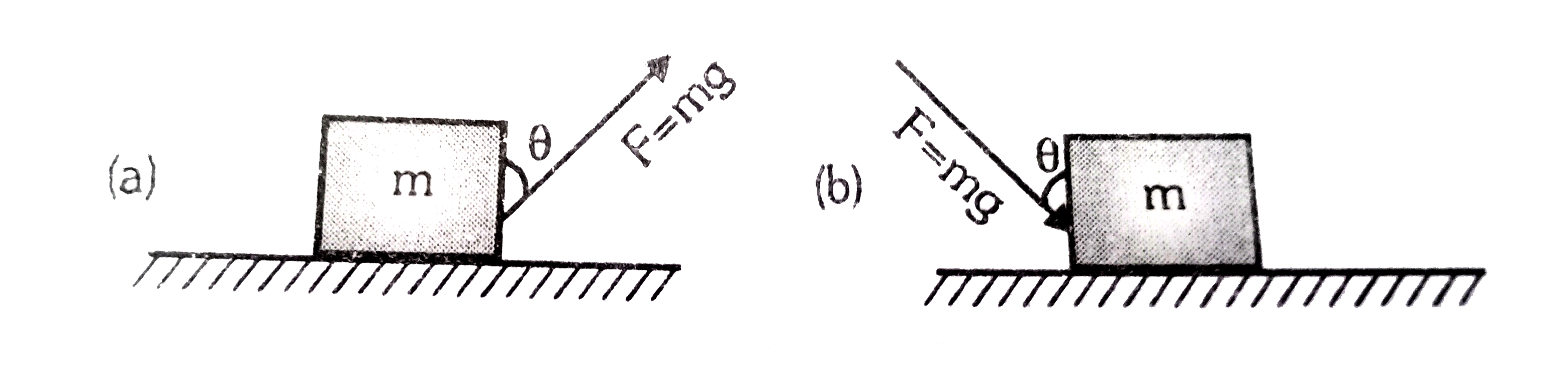
View SolutionA block of mass m rests on a rough horizontl surface as shown in figure (a) and (b). Coefficient of friciton between block and surface is μ. A force F-mg acting at an angle θ with the vertical side of the block. Find the condition for which block will move along the surface.
View Solution
Knowledge Check
In the situatiobn shown in the figure the friction coefficient between M and the horizontal surface is μ. The force F is applied at an angle θ with vertical. The correct statements are :
 AIf θ>tan−1 the block cannot be pushed forward for any value of FBIf θ<tan−1μ the block cannot be pushed forward for any value of FCAs θ decreases the magnitude of force needed to just push the block M forward increasesDNone of these
AIf θ>tan−1 the block cannot be pushed forward for any value of FBIf θ<tan−1μ the block cannot be pushed forward for any value of FCAs θ decreases the magnitude of force needed to just push the block M forward increasesDNone of theseIn the arrangement shown in figure the wall is smooth and friction coefficient between the blocks is μ=0.1. A horizontal force F=1000N is applied on the 2kg block. The wrong statement is :
 AThe normal interaction force between the blocks is 1000N.BThe friction force between the blocks is zero.CBoth the blocks accelerate downward with acceleration gm/s2DBoth the blocks remain at rest
AThe normal interaction force between the blocks is 1000N.BThe friction force between the blocks is zero.CBoth the blocks accelerate downward with acceleration gm/s2DBoth the blocks remain at restA block of mass M is at rest on a rough horizontal surface. The coefficient of friction between the block and the surface is μ. A force F = Mg acting at an angle θ with the vertical side of the block pulls it. In which of the following cases, the block can be pulled along the surface?
Atanθ≥μBcotθ≥μCtanθ/2≥μDcotθ/2≥μ
In the arrangement shown in figure, coefficient of friction between the two blocks is μ=1/2. The force of friction acting between
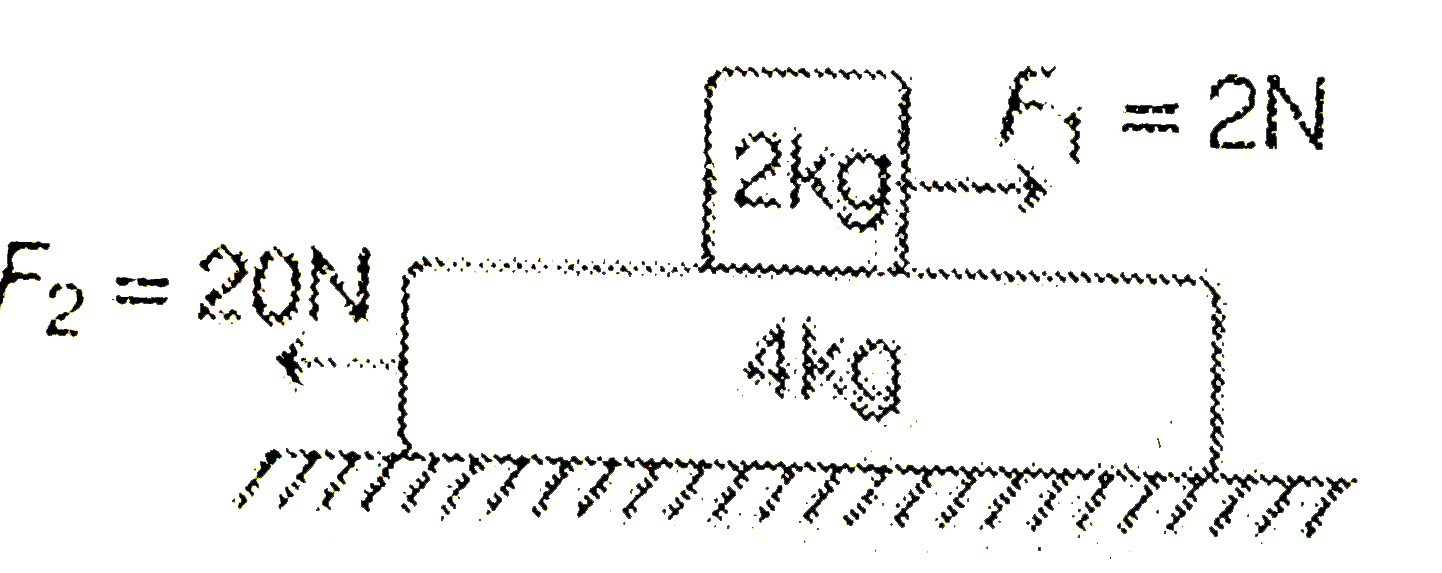
View SolutionA triangular block mass m rests on a fixed rough inclined plane having friction coefficient μ with the block. A horizontal force F is applied to it as shown in figure below, then the correct statement is :
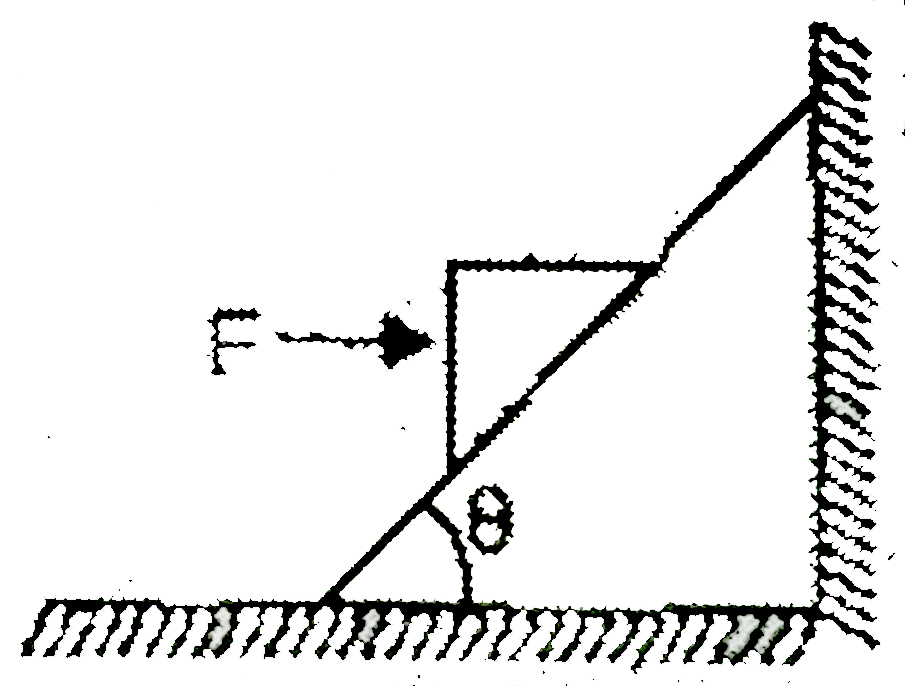
View SolutionA triangular block of mass m rests on a fixed rough inclined plane having friction coefficient μ with the block. A horizontal forces F is applied to it as shown in figure below, then the correct statements is:

View SolutionA block of mass M rests on a rough horizontal surface as shown. Coefficient of friction between the block and the surface is μ. A force F=mg acting at angle θ with the vertical side of the block pulls it. In which of the following cases the block can be pulled along the surface?

View Solution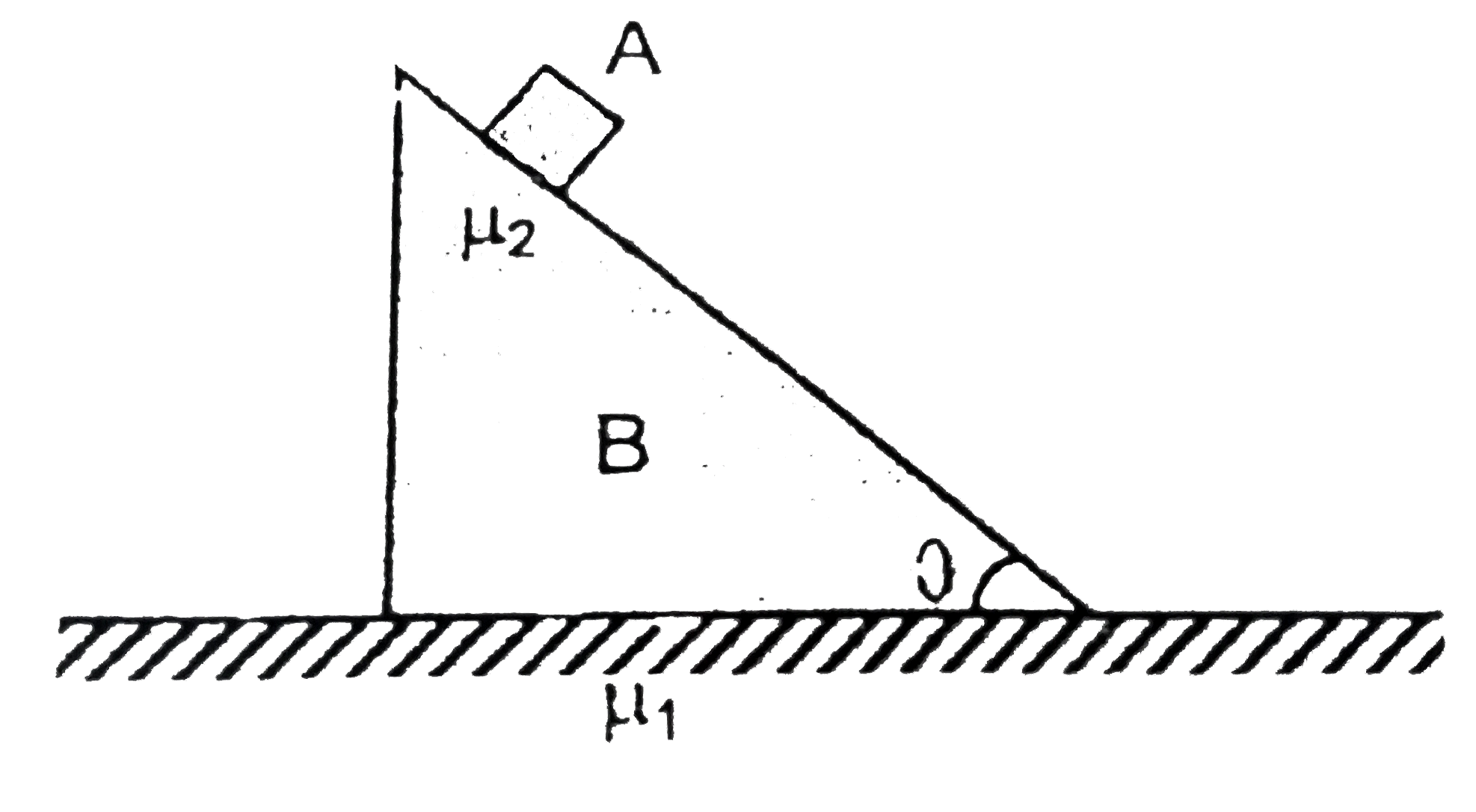
A wedge B of mass 2 m is placed on a rough horizontal suface. The coefficient of friction between wedge and the horizontal surface is μ1. A block of mass m is placed on wedge as shown in the figure. The coefficient of friction between block and wedge is μ2. The block and wedge are released from rest.
Q. Suppose the inclined surface of the wedge is at θ=37∘ from angle from horizontal and μ2=0 are wedge will remain in equilibrium if
View Solution
