A triangular block of mass m rests on a fixed rough inclined plane having friction coefficient μ with the block. A horizontal forces F is applied to it as shown in figure below, then the correct statements is:

Friction force is zero when Fcosθ=mgsinθ
The value of limiting friction is μ(mgsinθ+Fcosθ)
Normal reaction on the block is Fsinθ+mgcosθ
The value of limiting friction is μ(mgsinθ−Fcosθ)
The correct Answer is:A, C

N=mgcosθ+Fsinθ
Also if mgsinθ=Fcosθ then the friction force acting on the block is zero.
fstatic]maximum=μN=μ(mgcosθ+Fsinθ)
(The maximum static friction that can act on a body under a given solutions is known as limiting friction under the given conditions.)
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions6videos
FRICTION
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Integer type questions14videos
FRICTION
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I6videos
FRICTION
- BOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Level-II (H.W)54videos
COLLISION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EXERCISE -IV40videos
GRAVITATION
Similar Questions
A block of mass 10 kg is kept on a fixed rough (μ=0.8) inclined plane of angle of inclination 30∘. The frictional force acting on the block is
 View Solution
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View Solution
Knowledge Check
- Question 1 - Select One
A triangular block mass m rests on a fixed rough inclined plane having friction coefficient μ with the block. A horizontal force F is applied to it as shown in figure below, then the correct statement is :
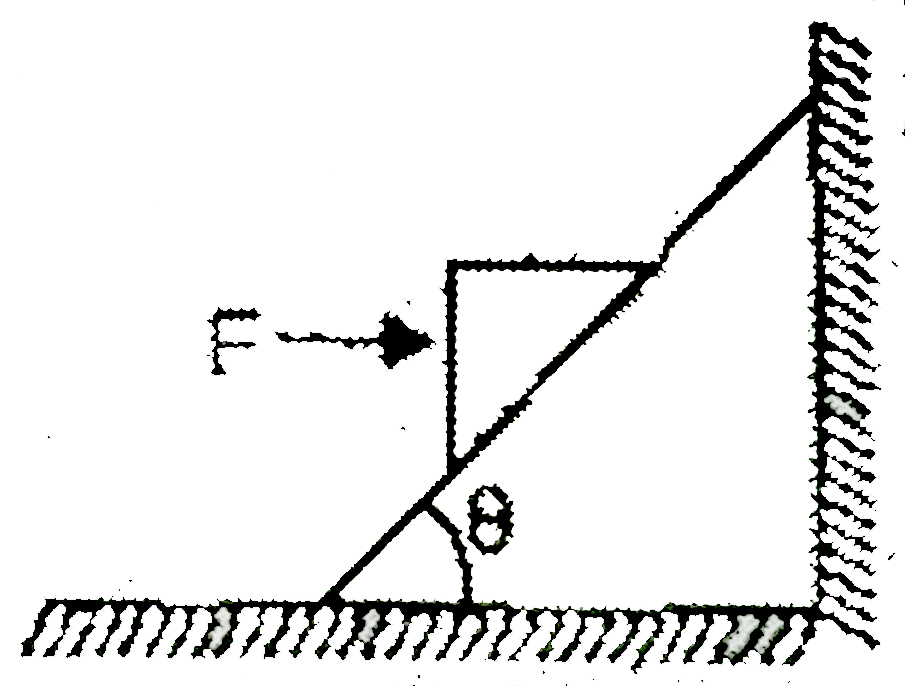 AFriction force is zero when Fcosθ=mgsinθBThe value of limiting friction is μ(mgsinθ+Fcosθ)CNormal reaction on the block is Fsinθ+mgcosθDThe value of limiting friction is μ(mgsinθ−Fcosθ)
AFriction force is zero when Fcosθ=mgsinθBThe value of limiting friction is μ(mgsinθ+Fcosθ)CNormal reaction on the block is Fsinθ+mgcosθDThe value of limiting friction is μ(mgsinθ−Fcosθ) - Question 2 - Select One
A block of mass m is at rest on a rough inclined plane, whose friction coefficient is μ. Net force exerted by surface on block is :-
AmgBmg sin θCμmgcosθDμmgsinθ - Question 3 - Select One
In the arrangement shown in figure the wall is smooth and friction coefficient between the blocks is μ=0.1. A horizontal force F=1000N is applied on the 2kg block. The wrong statement is :
 AThe normal interaction force between the blocks is 1000N.BThe friction force between the blocks is zero.CBoth the blocks accelerate downward with acceleration gm/s2DBoth the blocks remain at rest
AThe normal interaction force between the blocks is 1000N.BThe friction force between the blocks is zero.CBoth the blocks accelerate downward with acceleration gm/s2DBoth the blocks remain at rest
A cubical block of side L rests on a rough horizonta surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
 View Solution
View SolutionA cubical block of side L rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of frictions sufficienty high so that the block does not slide before toppling, the minimum force required to topple the block is :
 . View Solution
. View SolutionA cubical block of side L rests on a rough horizonta surface with coefficient of friction μ. A horizontal force F is applied on the block as shown. If the coefficient of friction is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
 View Solution
View SolutionA block of mass m in the equilib rium on a rough inclined plane with inclination α and coefficient of friction as shown in the figure (μ<tanα). A force F is applied on the block which makes an angle θ with the horizontal as shown in diagram.
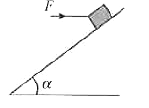 View Solution
View SolutionA block of weight W is kept on a rough horizontal surface (friction coefficient μ). Two forces W/2 each are applied as shown in the choose the correct statement
 .View Solution
.View Solution

