In YDSE of equal width slits, if intensity at the center of screen is I0, then intensity at a distance of β/4 from the central maxima is
I0
I02
I04
I03
The correct Answer is:b
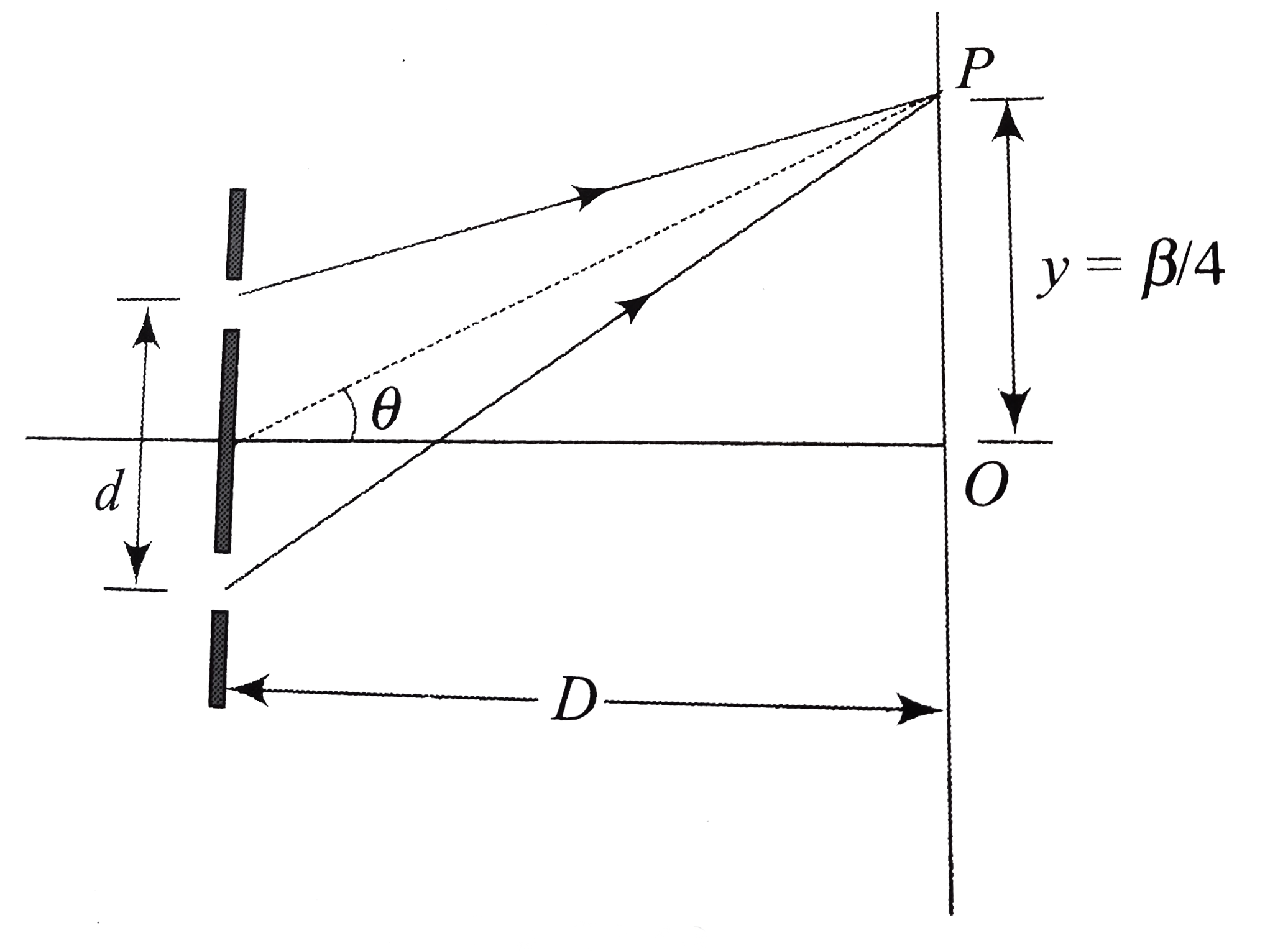
Let the intensity of individual waves be. I Then
I0=4I⇒I=I04
At P,
Δx=dsinθ
⇒Δxdsinθ=dyD
⇒Δx=dD×β4=dD×λD4d=λ4
∴Δϕ=2πλ×π4=π2 [Δϕ=kΔx]
I'=I+I+2√I2cos(π2)=2I=I02
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Multiple Correct
8 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
Monochromatic light of wavelength 5000 Å is used in Y.D.S.E., with slit-width, d = 1mm, distance between screen and slits, D = 1m. If intensity at the two slits are I1=4I0,I2=I0, find
distance of 5th minima from the central maxima on the screen
View SolutionThe wavelength of light used in a biprism experiment is 6000Å and Io is the intensity of central maximum. If distance between two slits is 0.25 cm and the distance of the screen from slits is 120 cm then at what distance (in um ) from the central maxima, the intensity will be I02 ?
View Solution
Knowledge Check
In YDSE, having slits of equal width, let β be the fringe width and I0 be the maximum intensity. At a distance x from the central brigth fringe, the intensity will be
AI0cos(xβ)BI0cos2(2πxβ)CI0cos2(πxβ)DI04cos2(πxβ)In a double slit experiment ,the separation between the slits is d=0.25cm and the distance of the screen D=100cm from the slits .if the wavelength of light used in λ=6000Åand I0is the intensity of the central bright fringe.the intensity at a distance x=4×10−5in form the central maximum is-
AI0BI0/2C3I0/4DI0/3In Young's double-slit experiment d/D=10−4 (d = distance between slits, D = distance of screen from the slits) At point P on the screen, resulting intensity is equal to the intensity due to the individual slit I0. Then, the distance of point P from the central maximum is (λ=6000Å)
A2 mmB1 mmC0.5 mmD4 mm
In a double slit experiment, the separation between the slits is d and distance of the screen from slits is D. If the wavelength of light used is λ and I is the intensity of central bright fringe, then intensity at distance from central maximum is
View SolutionIn a double slit experiment ,the separation between the slits is d=0.25cm and the distance of the screen D=100cm from the slits .if the wavelength of light used in λ=6000Åand I0is the intensity of the central bright fringe.the intensity at a distance x=4×10−5in form the central maximum is-
View SolutionIn a double slit experiment, the separation between the slits is d and distance of the screen from slits is D. If the wavelength of light used is λ and I is theintensity of central bright fringe, then intensity at distance from central maximum is
View SolutionIn Young's double slit experiment, the distance between the two slits is 0.1 mm, the distance between the slits and the screen is 1 m and the wavelength of the light used is 600 nm. The intensity at a point on the screen is 75% of the maximum intensity. What is the smallest distance of this point from the central fringe ?
View SolutionIn YDSE intensity at central maxima is I0 The ratio II0, at path difference λ8 on the screen from central maxima , is closed to
View Solution
