In Young.s double slit experiment, blue-green light of wavelength 500nm is used. The slits are 1.20mm apart, and the viewing screen is 5.40m away from the slits. What is the fringe width.
6.2mm
4.2mm
2.25mm
1.25mm
The correct Answer is:C
To find the fringe width in Young's double slit experiment, we can use the formula:
x=λDd
where:
- x is the fringe width,
- λ is the wavelength of the light,
- D is the distance from the slits to the screen,
- d is the distance between the slits.
Step 1: Convert the given values to standard units
1. Wavelength (λ): Given as 500 nm.
λ=500nm=500×10−9m
2. Distance between the slits (d): Given as 1.20 mm.
d=1.20mm=1.20×10−3m
3. Distance to the screen (D): Given as 5.40 m.
D=5.40m
Step 2: Substitute the values into the formula
Now, substituting the values into the fringe width formula:
x=(500×10−9)×5.401.20×10−3
Step 3: Calculate the fringe width
1. Calculate the numerator:
500×10−9×5.40=2.7×10−6m
2. Now, divide by d:
x=2.7×10−61.20×10−3=2.25×10−3m
Step 4: Convert to millimeters
To convert meters to millimeters:
x=2.25×10−3m=2.25mm
Conclusion
Thus, the fringe width x is:
2.25mm
- x is the fringe width,
- λ is the wavelength of the light,
- D is the distance from the slits to the screen,
- d is the distance between the slits.
1. Wavelength (λ): Given as 500 nm.
λ=500nm=500×10−9m
2. Distance between the slits (d): Given as 1.20 mm.
d=1.20mm=1.20×10−3m
D=5.40m
Now, substituting the values into the fringe width formula:
x=(500×10−9)×5.401.20×10−3
1. Calculate the numerator:
500×10−9×5.40=2.7×10−6m
x=2.7×10−61.20×10−3=2.25×10−3m
To convert meters to millimeters:
x=2.25×10−3m=2.25mm
Thus, the fringe width x is:
2.25mm
Topper's Solved these Questions
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -II (DIFFRACTION)
17 Videos
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -II (POLARISATION)
10 Videos
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -IB (ASSERTION AND REASON)
67 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
In the Young’s double slit experiment, for which colour the fringe width is least
View SolutionYoung’s double slit experiment is performed with light of wavelength 550 nm . The separation between the slits is 1.10mm and screen is placed at distance of 1 m . What is the distance between the consecutive bright or dark fringes
View SolutionIn Young.s double slit experiment sodium light is replaced by blue lamp, then the fringe width
View SolutionIn Young's double slit experiment, the two slits 0.15mm apart are illuminated by light of wavelength 450nm. The screen is 1.0m away from the slits. Find the distance of second bright fringe and second dark fringe from the central maximum. How will the fringe pattern change if the screen is moved away from the slits ?
View Solution(a) In Young.s double slit experiment using monochromatic light of wavelength 600 nm, interference pattern was obtained on a scren kept 1.5 m away from the plane of the two slits. Calculate the distance between the two slits. Fringe separation/fringe width was found to be 1.0 mm.
(b) When a fish is observed underwater at depth of 3 m appears to be at a depth of 2 m. What is the refractive index of water ?
View SolutionIn Young’s double slit experiment, using light of wavelength 600 nm, 10th bright fringe is obtained on a screen, 3mm from the centre of the pattern. If the screen is 120 cm away from the slits, calculate:
(i) Distance between the two slits,
(ii) Fringe width, i.e. fringe separation.
View SolutionIn a Young's double slit experiment , the slits are Kept 2mm apart and the screen is positioned 140cm away from the plane of the slits. The slits are illuminatedd with light of wavelength 600nm. Find the distance of the third brite fringe. From the central maximum . in the interface pattern obtained on the screen frings from the central maximum. 3
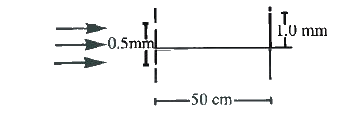
View SolutionWhite coheral light (400 nm 700 nm ) is sent through the slit of a Young.s double slit experiment. The separation between the slits is 0.5 mm and the screen is 50 away from the slits . There is a hole in the screen at a point 1.0 mm away (along the width of the fringes) from the central line. Which wavelengths (s) will be absent in the light coming from the hole ?
View SolutionIn Young's double slit experiment , the two slits 0.20 mm apart are illuminated by monochromatic light of wavelength 600 nm . The screen 1.0 m away from the slits .
(a) Find the distance of the second (i) bright fringe , (ii) dark fringe from the central maximum .
(b) How will the fringe pattern change if the screen is moved away from the slits ?
View SolutionIn Young's double slit experiment the two slits 0.12 mm apart are illuminated by monochromatic light of wavelength 420 nm. The screen is 1.0 m away from the slits .
(a) Find the distance of the second (i) bright fringe , (ii) dark fringe from the central maximum .
(b) How will the fringe pattern change if the screen is moved away from the slits ?
View Solution
