In Young's experiment, find the distance between two slits that results in the third minimum for $420 n m$ violet light at an angle $30^{\circ}$
.

Video Solution

Text Solution

Verified by Experts

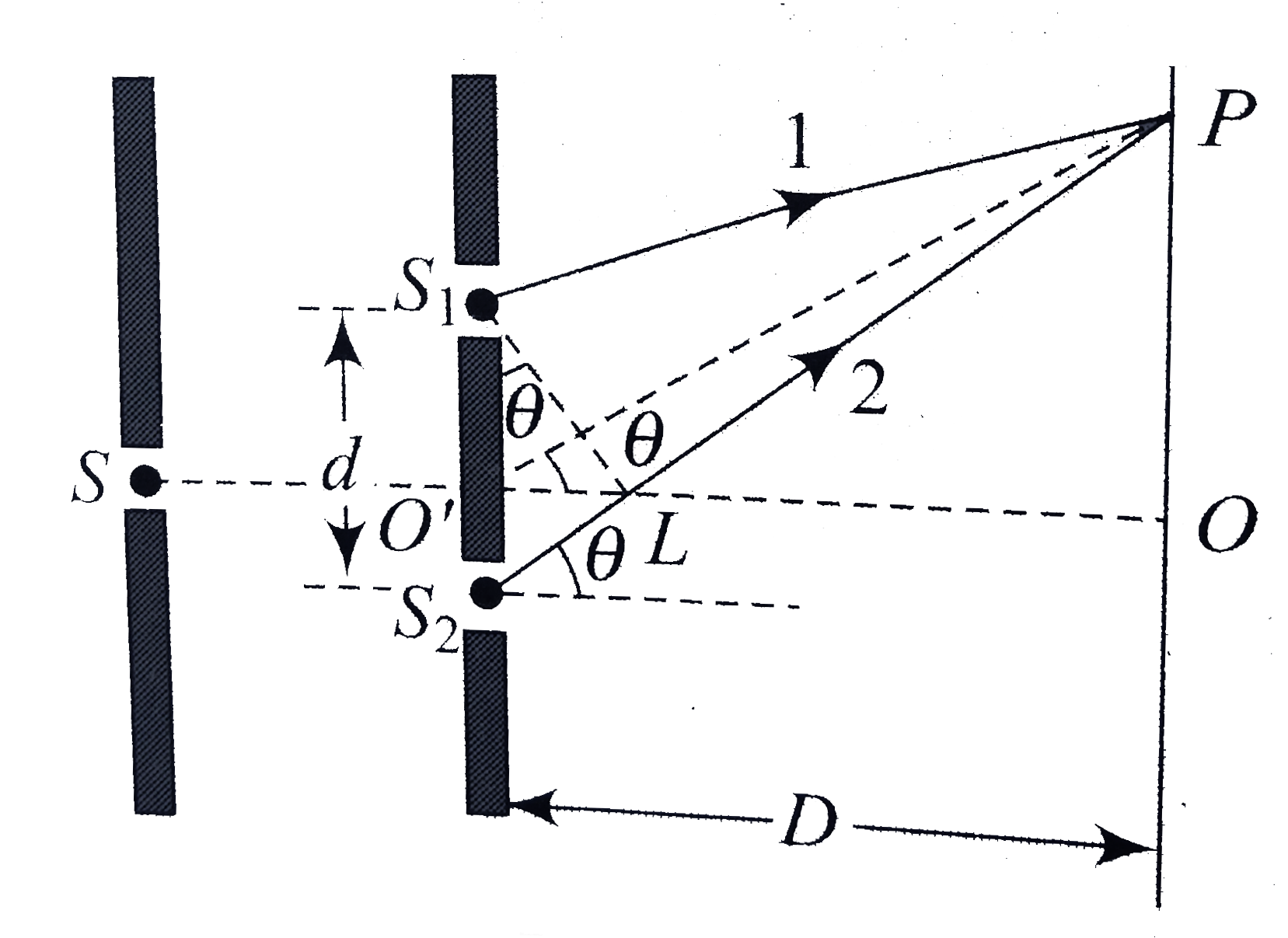$S_{2} L = d sin θ$
or $Δ x = d sin θ$
For intensity to be minimum,
$Δ x = sin θ$
$Δ x = (2 n - 1) λ / 2$
$n = 1, 2, 3, \dots$
For third minimum, $n = 3$
$d sin θ = \frac{5 λ}{2}$
Given: $λ = 420 n m = 420 \times 10^{- 9} m$
$θ = 30^{\circ}$
$∴ d {sin 30}^{\circ} = \frac{5}{2} \times 420 \times 10^{- 9} \Rightarrow d = 2.1 \times 10^{- 6} m$ .

|

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In Young's double slit experiment, the distance between two slits is made three times then the fringe width will becomes
A9 times
B1/9 times
C3 times
D1/3 times
Question 2 - Select One
In Young’s double slit experiment, the distance between the two slits is made half, then the fringe width will become
AHalf
BDouble
COne fourth
DUnchanged
Question 3 - Select One
In Young's double slit experiment, if the distance between two slits is equal to the wavelength of used light. Then the maximum number of bright firnges obtained on the screen will be
AInfinite
B3
C4
D5

CENGAGE PHYSICS-WAVE OPTICS-Exercise 2.2

Home
Ask Doubt
Profile