In YDSE with d=1mm and D=1m, Slabs of (t=1μm,μ=3) and (t=0.5μm,μ=2) are introduced in front of upper and lower slits, respectively. Find the shift in the fringe pattern.
Optical path for light coming form upper slit S1 is
S1p+1μm×(2−1)−S2P+0.5μm
Similarly, optical path for light coming from S2 is
S2P+0.5μm×(2−1)=S2P+0.5μm
Path difference :
Δx=(S2P+0.5μm)−(S1P+2μm
=(S2P−S1P)−1.5μm
=ydD−1.5μm
For Central bright fringe, Δx=0
⇒y=1.5μm1mm×1m=1.5mm
The whole pattern is shifted by 1.5 mm upward.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Subjective
11 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Single Correct
128 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.1
12 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
A monochromatic light of wavelength 5000Å incident normally on slit plane of YDSE setup. If d=5×10−4m and D = 1 m and a thin film thickness 1.5×10−6m and μ=1.5 is place in front of one of the slits, find intensity of light at the centre of screen if each slit produces an intensity I0 on screen. [0]
View Solution(a) How many bright fringes appear between the first diffraction-envelope minima to either side of the central maximum in a double-slit pattern if λ550nm, d = 0.180 mm, and a=30.0μm? (b) What is the ratio of the intensity of the third bright fringe to the intensity of the central fringe?
View Solution
Knowledge Check
In YDSE, let A and B be two slits. Films of thickness tA and tB and refractive μA and μB are placed in front of A and B, respectively. If μAtA=μAtB, then the central maxima will
Anot shiftBshift toward ACshift toward BD(b) if tB<tA and (C ) if tB<tAIf refractive index of core & cladding are μ1&μ2 respectively then :
Aμ1>μ2Bμ2>μ1Cμ1=μ2DNone of theseIf refractive index of core & cladding are μ1 & μ2 respectively then :
Aμ1>μ2Bμ2>μ1Cμ1=μ2DNone of these
Figure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.
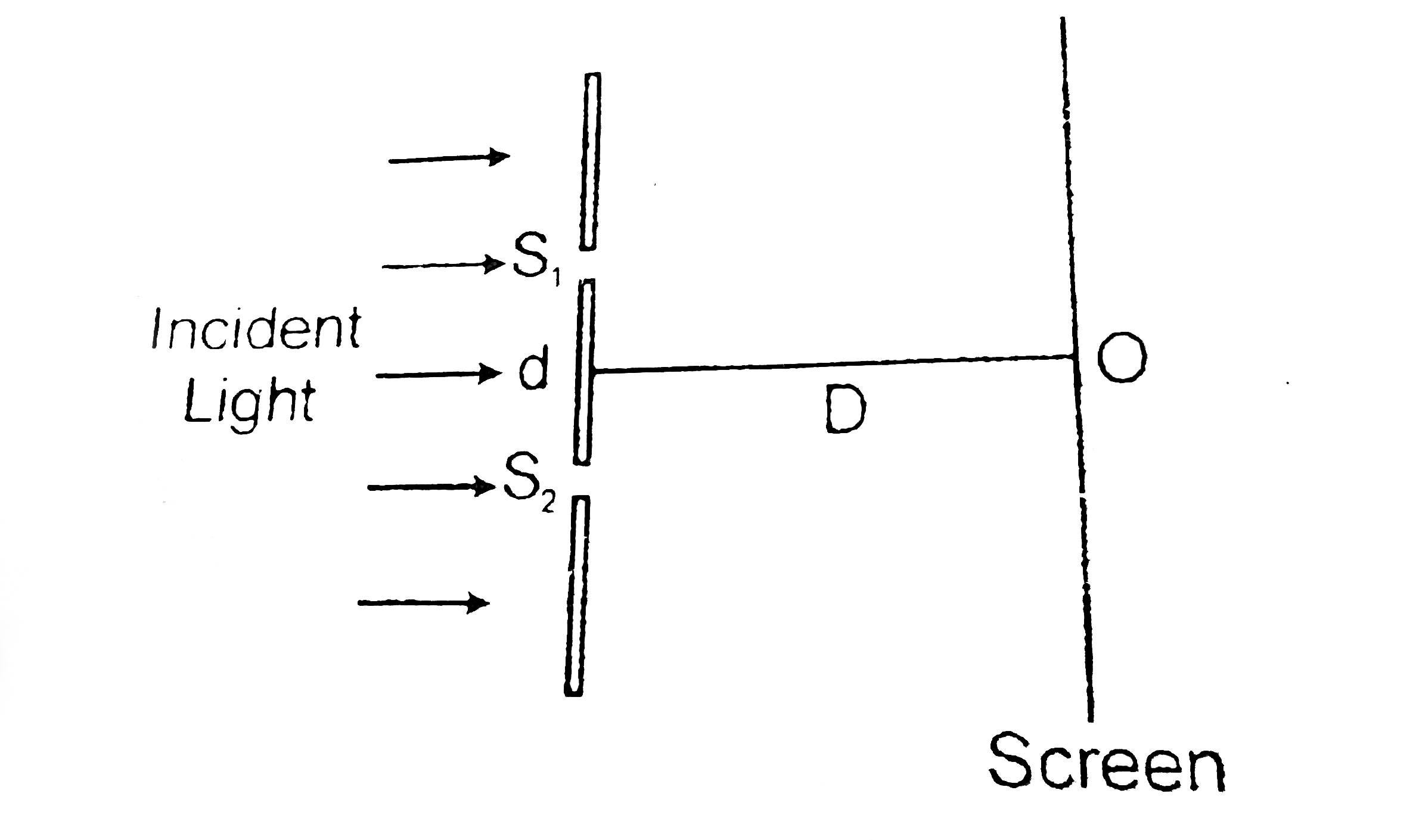
Due to placement of film in front of S1, how many bright fringes cross the point O of screen excluding the one which was at O earlier :
View SolutionFigure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.
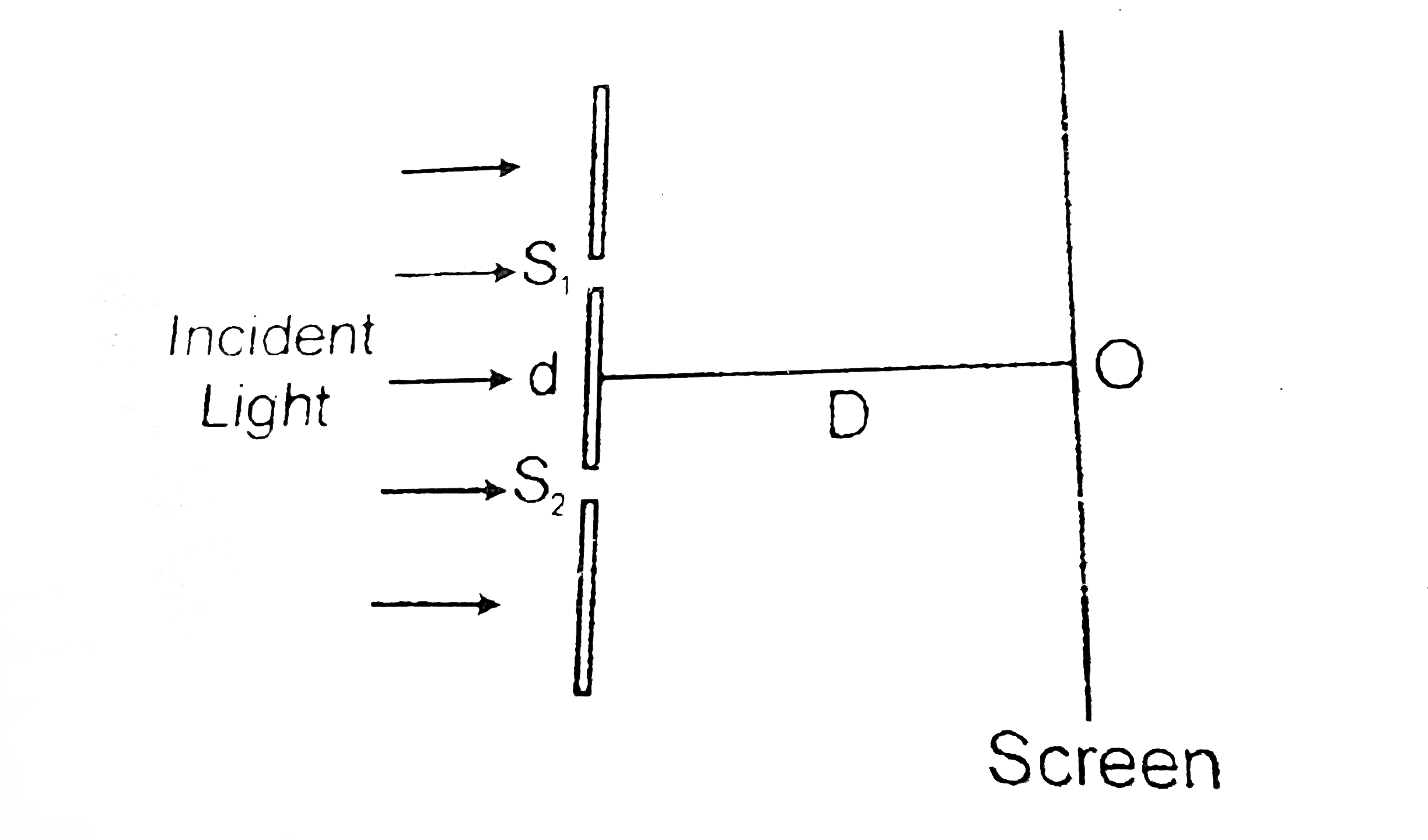
After placing the film of slit S1, the intensity at point O screen is :
View SolutionIn a modified YDSE, the region between the screen and slits is immersed in a liquid whose refractive index varies with time as μ1=(5/2)−(T/4) until it reaches s steady state value of 5/4. A glass plate of thickness 36 μm and refractive index 3/2 is introduced in front of one of the slits.
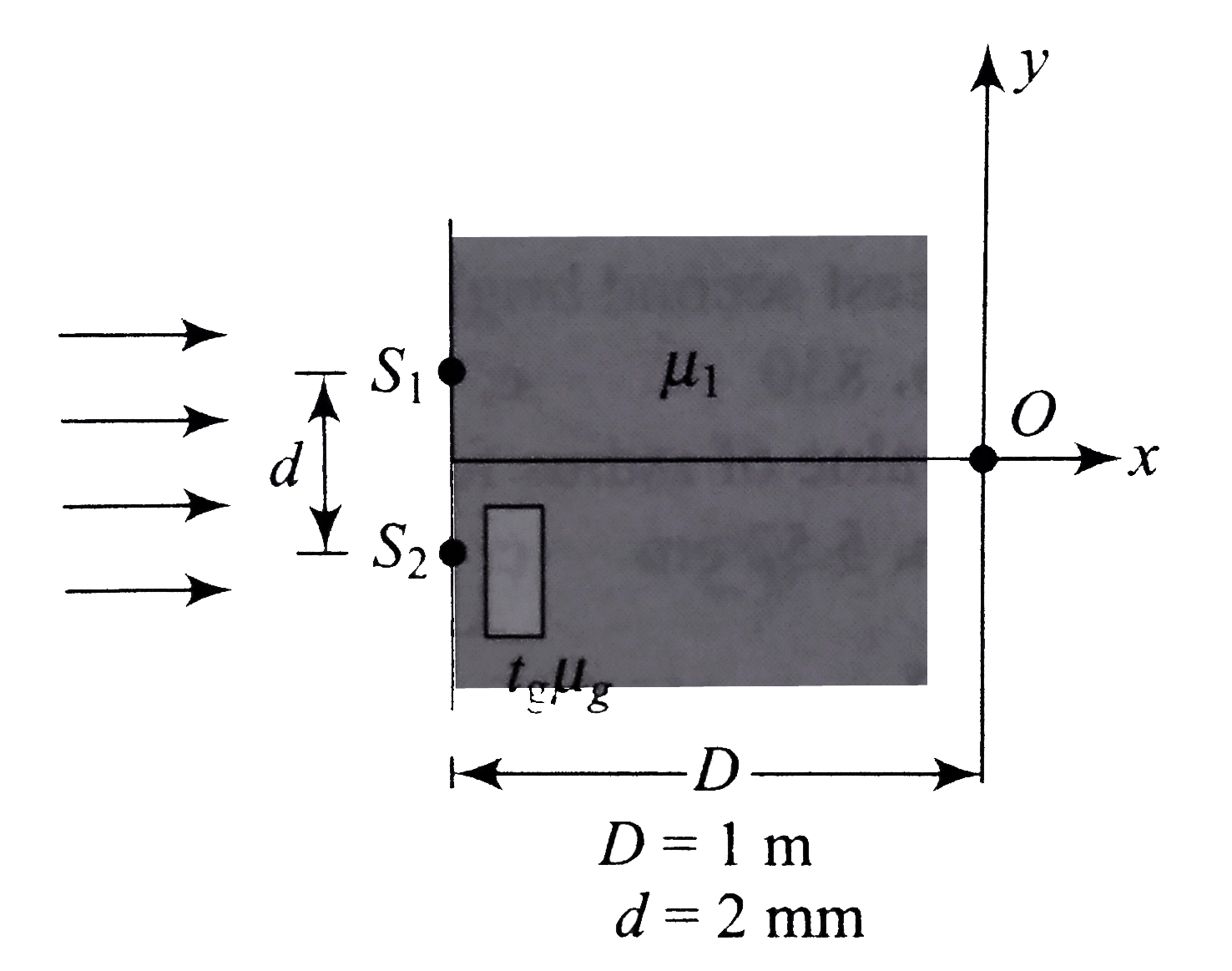
Find the time when central maxima is at point O. located symmetrically on the x-asix.
View SolutionIf a transparent medium of refractive index μ=1.5 and thickness t=2.5×10−5m is inserted in front of one of the slits of Young's Double Slit experiment, how much will be the shift in the interference patten? The distance between the slits is 0.5mm and that between slits and screen is 100cm
View SolutionIn a modified YDSE, the region between the screen and slits is immersed in a liquid whose refractive index varies with time as μ1=(5/2)−(T/4) until it reaches s steady state value of 5/4. A glass plate of thickness 36 μm and refractive index 3/2 is introduced in front of one of the slits.

What is the speed of the central maxima when it is at
View Solution
