Initially a sphere of radius r is rotating with an angular velocity ω about its own horizontal axis. When the sphere falls on a surface (coefficient of friction μ), then it begins to skid first and then starts rotating without skidding.
How much distance will the sphere cover before reaching this velocity?
Distance covered,
x=12at2=12μg(2ωr7μg)2=249.r2ω2μg.
Topper's Solved these Questions
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - Section Related Question
2 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
20 Videos
- QUESTION PAPERS OF WBCHSE -2018BOOK - CHHAYA PUBLICATIONCHAPTER - QUESTION PAPERS OF WBCHSE -2018EXERCISE - SECTION -II
20 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER
16 Videos
Similar Questions
A solid sphere is rotating with a constant angular velocity about an axis touching the surface. Its angular momentum will be:
View SolutionA ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View Solution
Knowledge Check
A ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
AωoμkR2gBωog2μkRC2ωoRμkgDωoR2μkgA ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
Aω0μkR2gBω0g2μkRC2ω0RμkgDω0R2μkgA solid sphere is rotating with a constant angular velocity about an axis touching the surface. Its angular momentum will be:
A23MR2ωB57MR2ωC75MR2ωD52MR2ω
A uniform sphere of radius a rotating with an angular velocity ω about an axis perpendicualr to the plane of motion and its cener impinges on a horizontal plane, let u and v are horizontal and vertical component of velocity before impact. Then
View SolutionA ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View SolutionA sphere of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then initally
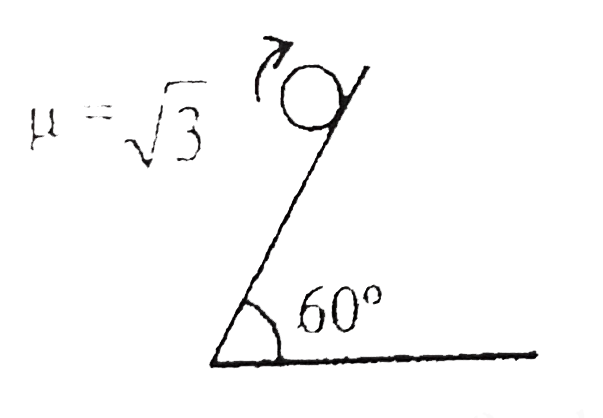
View SolutionA cylinder full of water is rotating about its own axis with uniform angular velocity ω. Then the shape of free surface of water will be
View SolutionA uniform circular ring of radius R is first rotated about its horizontal axis with an angular velocity ω0 and then carefully placed on a rough horizontal surface as shown. The coefficient of friction between the surface and the rings μ. Time after which its angular speed is reduced to 0.5ω0 is

View Solution
