Internal energy of an ideal diatomic gas at 300 K is 100 J. In this 100 J
potential energy = 0
rotational kinetic energy = 40 J
translational kinetic energy = 60 J
translational kinetic energy is 100 J
The correct Answer is:A, B, C
To solve the problem of determining the distribution of internal energy in an ideal diatomic gas at 300 K, we can follow these steps:
Step 1: Understand the Degrees of Freedom
For a diatomic gas, the degrees of freedom (DOF) are:
- Translational: 3 (movement along x, y, and z axes)
- Rotational: 2 (rotation about two axes perpendicular to the bond axis)
- Total DOF = 5
Hint: Remember that each degree of freedom contributes 12kBT to the internal energy, where kB is the Boltzmann constant and T is the temperature in Kelvin.
Step 2: Calculate the Total Internal Energy
The total internal energy U of the gas can be expressed as:
U=f2kBT
where f is the total degrees of freedom. Given U=100J and f=5, we can set up the equation:
100=52kBT
Hint: Rearranging the equation will help you isolate kBT.
Step 3: Solve for kBT
Rearranging the equation gives:
kBT=2×1005=40J
Hint: Make sure to double-check your arithmetic when calculating kBT.
Step 4: Calculate the Rotational Kinetic Energy
The rotational kinetic energy Urot can be calculated using its degrees of freedom:
Urot=22kBT=1×kBT=40J
Hint: Remember that you only consider the rotational degrees of freedom (2 in this case).
Step 5: Calculate the Translational Kinetic Energy
The translational kinetic energy Utrans is given by:
Utrans=32kBT=32×40=60J
Hint: Again, focus on the translational degrees of freedom (3 in this case) when calculating.
Step 6: Determine Potential Energy
Since the problem states that the internal energy is entirely kinetic (for an ideal gas), the potential energy Upot is:
Upot=0J
Hint: In an ideal gas, potential energy changes are negligible, so it remains zero.
Summary of Results
- Total Internal Energy: 100J
- Rotational Kinetic Energy: 40J
- Translational Kinetic Energy: 60J
- Potential Energy: 0J
Final Answer:
- Potential Energy: 0J
- Rotational Kinetic Energy: 40J
- Translational Kinetic Energy: 60J
For a diatomic gas, the degrees of freedom (DOF) are:
- Translational: 3 (movement along x, y, and z axes)
- Rotational: 2 (rotation about two axes perpendicular to the bond axis)
- Total DOF = 5
The total internal energy U of the gas can be expressed as:
U=f2kBT
where f is the total degrees of freedom. Given U=100J and f=5, we can set up the equation:
100=52kBT
Rearranging the equation gives:
kBT=2×1005=40J
The rotational kinetic energy Urot can be calculated using its degrees of freedom:
Urot=22kBT=1×kBT=40J
The translational kinetic energy Utrans is given by:
Utrans=32kBT=32×40=60J
Since the problem states that the internal energy is entirely kinetic (for an ideal gas), the potential energy Upot is:
Upot=0J
- Total Internal Energy: 100J
- Rotational Kinetic Energy: 40J
- Translational Kinetic Energy: 60J
- Potential Energy: 0J
- Potential Energy: 0J
- Rotational Kinetic Energy: 40J
- Translational Kinetic Energy: 60J
Topper's Solved these Questions
Similar Questions
The internal energy of one mole of the diatomic gas at 200 K is
View SolutionKinetic energy of one of an ideal gas at 300 K in kJ is
View SolutionAn ideal gas follows a cyclic process as shown in figure. Internal energy of gas at point A is 10 J while at B is 70 J. the heat absorbed by gas in BC is 120 J.
(a) How much heat is absorbed in process AB?
(b) Find heat energy rejected or absorbed by gas in process CA.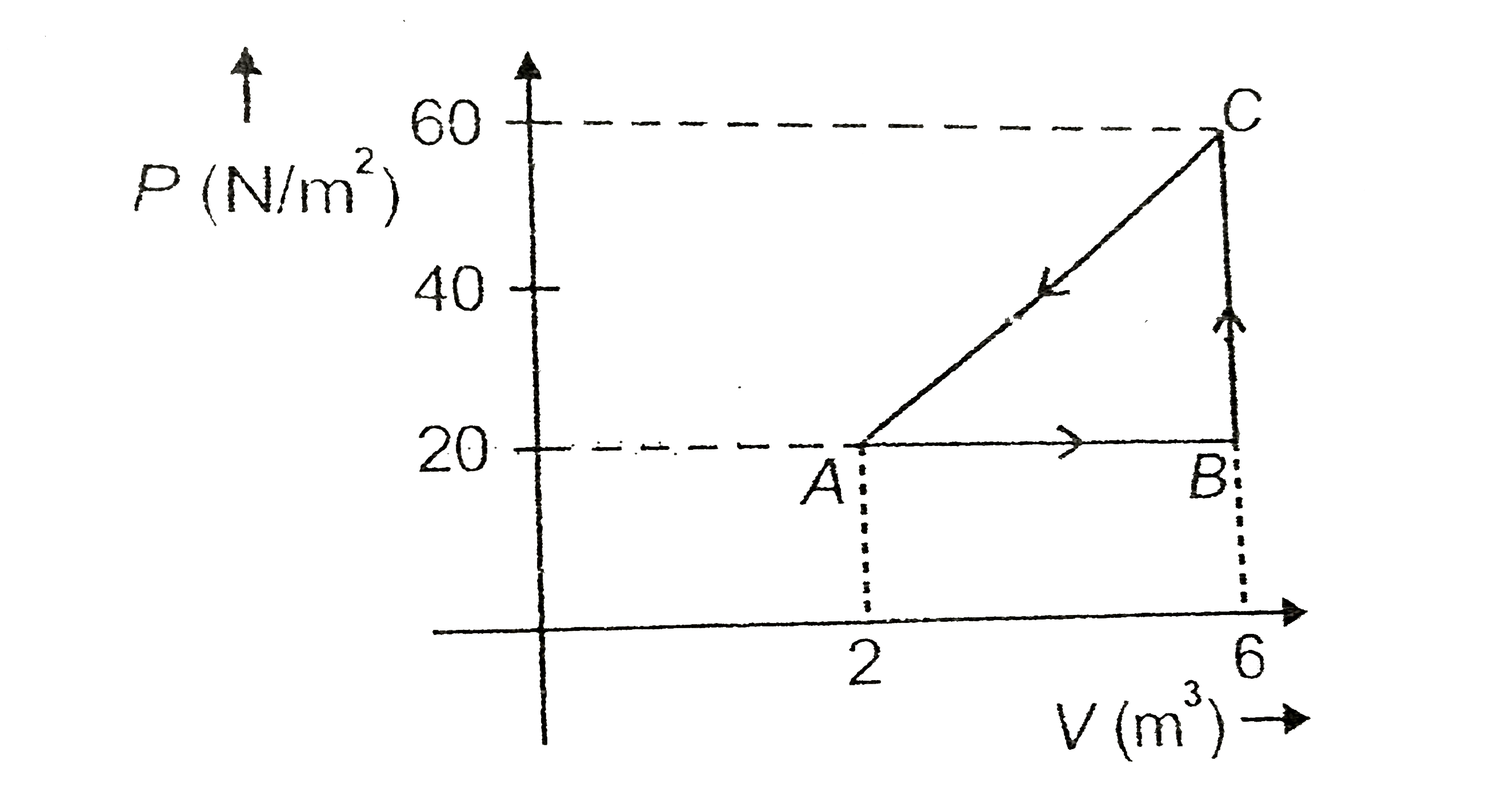
View SolutionThe given figure shown a change of state A to state C by two paths ABC and AC for an ideal gas. Calculate the :
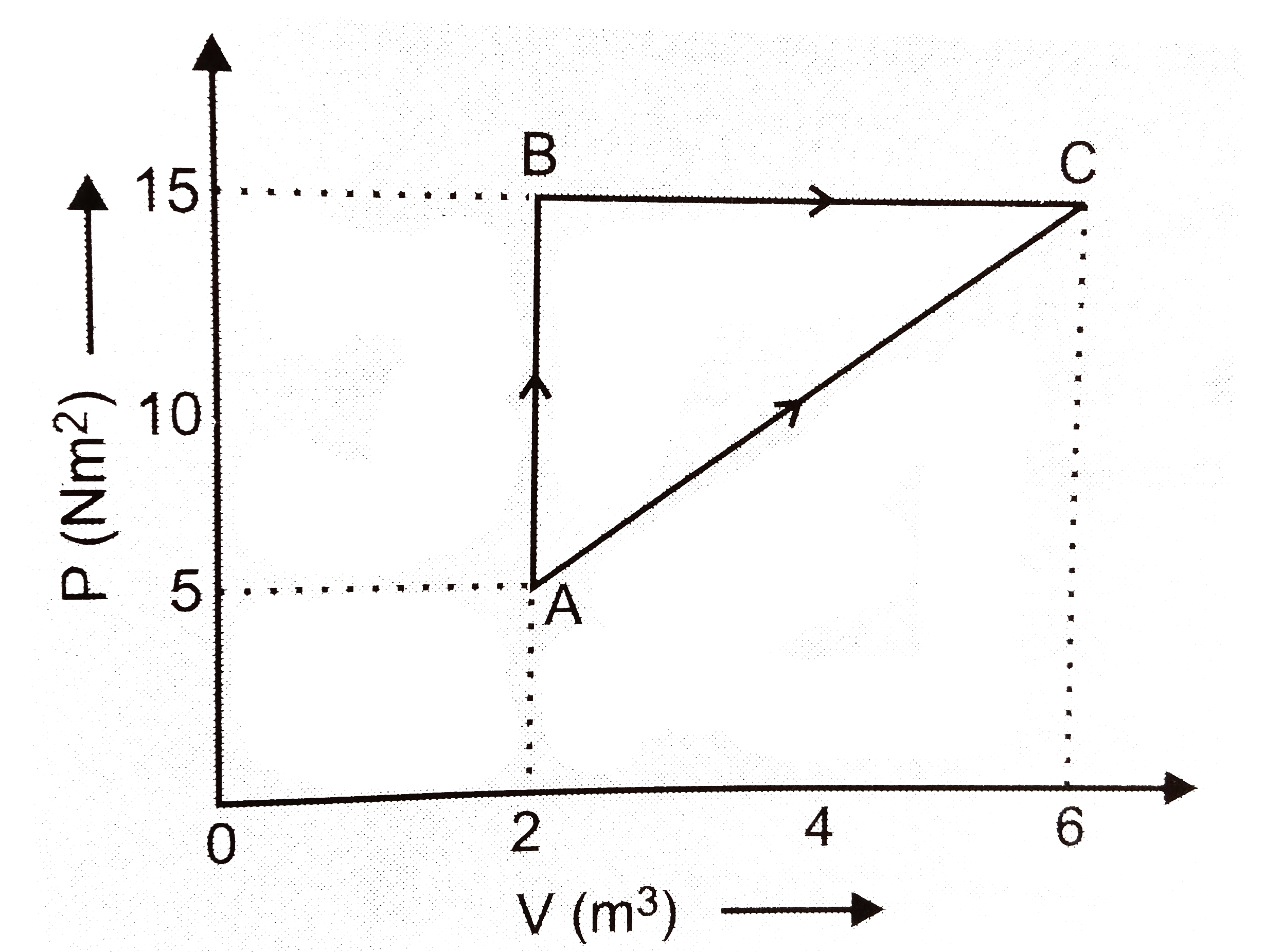
(a) Path along which work done is least.
(b) Internal energy at C if the internal energy of gas at A is 10J and amount of heat supplied to change its state to C through the path AC is 200J.
(c) Amount of heat supplied ot the gas to go from A to B, if internal energy of gas at state B is 10J.
View SolutionThe relationship between enthalpy and internal energy change is
View SolutionA system consisting of one mole of an ideal diatomic gas absorbs 200J of heat and does 50J of work on surroundings. What is the change in temperature if vibrational modes of motion are inactive?
View SolutionFind the change in internal energy if heat supplied to the gaseous system is 100 J and work done by the system is 80 J.
View SolutionFigure shows an ideal gas changing its state A to state C by two different path ABC and AC. The internal energy of the gas at A is 10J and the amount of heat supplied to change its state to C through the path AC is 200J. Find the internal energy at C.
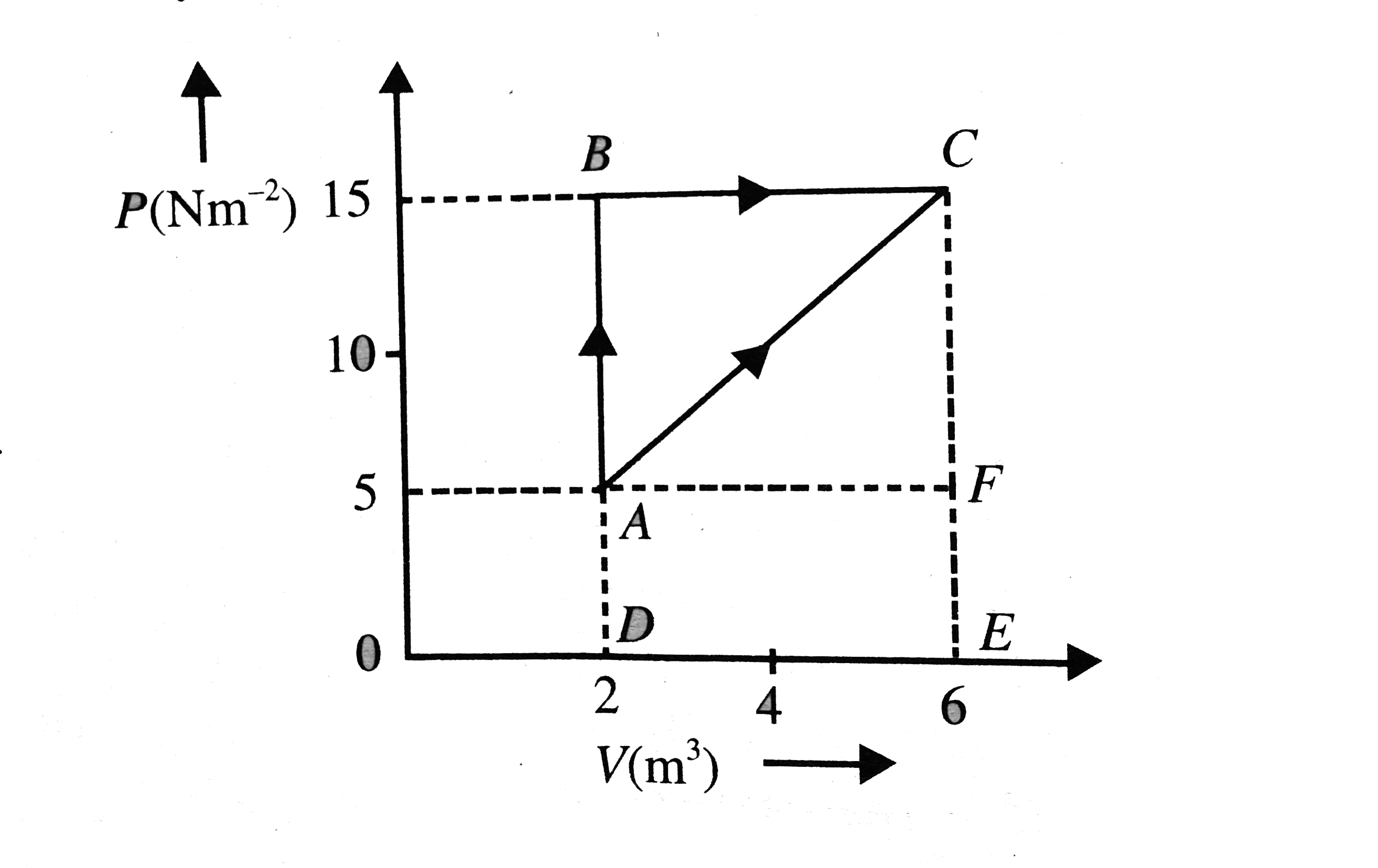
View SolutionIf 21 J of heat energy is supplied to an ideal diatomic gas at constant pressure, then the change in its energy is
View SolutionThe temperature of a ideal gas is increased for 100 k to 400k. If at 100 K the root mea square velocity of the gas molecules is v, at 400K it becomes
View Solution
