is a section of a condiucting rod of radius R1=1.30 mm and length L=11.0 m inside a thin-walled coaxial conducting cylinderical shell of radus R2=10.0R1and the (same) length L. The net charge on the rod is Q1=−5.22×10−13C, that on the shell is Q1=−2.00Q1. What are the (a) magnitude E and (b) direction (radially inward or outward) of the electric field at radial distacne r=2.00R2 ? What are (c ) E and (d) the direction at r=5.00R1 ? What is the charge on the (e) interior and (f) exterior surface of the shell ?

(a)3.28×10−2N/C,(b)outward, (c ) 0.131N/C,(d) inward, (e) +5.22×10−13C,(f)+5.22×10−13C
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)20videos
GAUSS' LAW
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)2videos
GAUSS' LAW
- BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - CHECKPOINT7videos
GAUSS' LAW
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)1videos
FORCE AND MOTION-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)3videos
GEOMETRICAL OPTICS : REFLECTION
Similar Questions
A spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?View SolutionInside a charged thin conducting shell of radius R, a point charge +Q is placed as shown in figure potential of shell may be
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A spherical conducting shell of radius r0 carry a charge q0. Then value of electric field inside it is :-
Akq0/r2Bkq0/r3CzeroDuniform but non zero - Question 2 - Select One
Consider two concentric spherical metal shells of radii r1 and r2(r2>r1). If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
A−r2r1qBzeroC−r1r2qD−q - Question 3 - Select One
The radii of two concentric spherical conducting shells are r1andr2(>r1). The change on the oute shell is q. The charge on the inner shell which is connected to the earth is
Aq(r2r1)Bq2(r1r2)C−q(r1/r2)Dq2(r2r1)
Inside a charged thin conducting shell of radius R, a point charge +Q is placed as shown in figure potential of shell may be
 View Solution
View SolutionIn figure , a solid sphere of radius a = 2.00cm is concentric with a spherical conductiosn shell of inner raedius b =2.00 a and outer radius c=2.40 a. the sphere has a net unifrom charge q1=+5.00C. The shell has a net charge q2=−q1. Distance (a) r=0 (b) r= a/2.00 (c) r=a (d) r = 1.50 a (e) r= 2.30a and (f) r= 3.50 a ? what si the net charge on the (g) inner and (h) outer surface of the shell ?
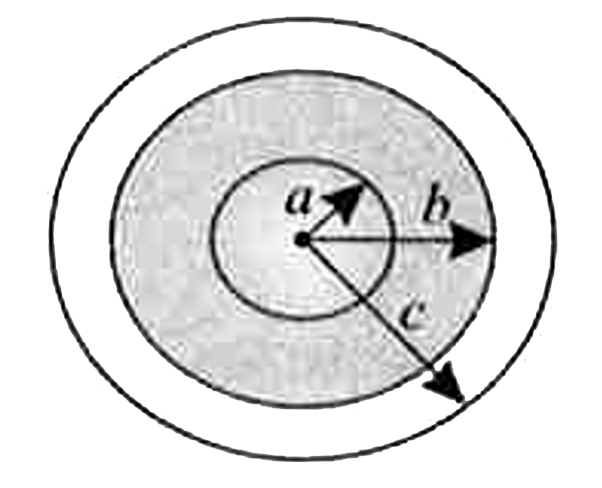 View Solution
View SolutionIn figure , a solid sphere of radius a = 2.00cm is concentric with a spherical conduction shell of inner radius b =2.00 a and outer radius c=2.40 a. the sphere has a net uniform charge q1=+5.00C. The shell has a net charge q2=−q1. Distance (a) r=0 (b) r= a/2.00 (c) r=a (d) r = 1.50 a (e) r= 2.30a and (f) r= 3.50 a ? what si the net charge on the (g) inner and (h) outer surface of the shell ?
 View Solution
View SolutionConsider two concentric spherical metal shells of radii r1 and r2(r2>r1). If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
View SolutionThe radii of two concentric spherical conducting shells are r1andr2(>r1). The change on the oute shell is q. The charge on the inner shell which is connected to the earth is
View Solution

