The box-like Gaussian surface encloses a net charge of +32ε0 C and lies in an electric field given by →E=[(10.0+2.00x)ˆi−3.00ˆj+bzˆk]N/C, with x and z in meters and b a constant. The bottom face is in the xz plane, the top face is in the horzontal plane passing through y2=1.00m, For x1=1.00m,x2=4.00m,z1=1.00m,andz2=3.00m, what is b ?
![The box-like Gaussian surface encloses a net charge of + 32 epsi (0) C and lies in an electric field given by vecE = [(10.0 + 2.00x)hati -3.00hatj+ bzhatk]N//C, with x and z in meters and b a constant. The bottom face is in the xz plane, the top face is in the horzontal plane passing through y(2) = 1. 00 m , For x (1) = 1. 00 m, x (2) = 4. 00m, z (1) =1.00 m, and z (2) = 3. 00 m, what is b ?](https://d10lpgp6xz60nq.cloudfront.net/physics_images/MST_AG_JEE_MA_PHY_V02_C23_E05_025_Q01.png)
3.33N/Cm
Topper's Solved these Questions
- GAUSS' LAW BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
20 Videos
- GAUSS' LAW BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
2 Videos
- GAUSS' LAW BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - CHECKPOINT
7 Videos
- FORCE AND MOTION-IIBOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
1 Videos
- GEOMETRICAL OPTICS : REFLECTION BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
Similar Questions
Knowledge Check
The equation of a plane passing throgh the points A(a,0,0),B(0,b,0) and C(0,0,c) is given by
Aax+by+cz=0Bax+by+cz=1Cxa+yb+zc=0Dxa+yb+zc=1Equation of plane passing through (0,0,a) and perpendicular to two planes x−y−z=0 and x−2y=0 is
Ax+y+z=0B2x+y+z=aCx+2y+z=aDx+y+z=2aThe centre of a circle passing through the points (0, 0), (1, 0) and touching the circle x2+y2=9, is
A(32,12)B(12,32)C(12,12)D(12,−21/2)
The equation of the plane passing through the intersection of x+2y+3z+4=0and4x+3y+2z+1=0 and the origin (0.0,0) is
View SolutionIn the given electric field →E=[(d+x)ˆi+E0ˆj]N/Ca hypothetical closed surface is taken as shown in figure. The total charge enclosed within the closed surface is Kε0. Then, find the value of k. (a=2m, b=3m and c=2m)
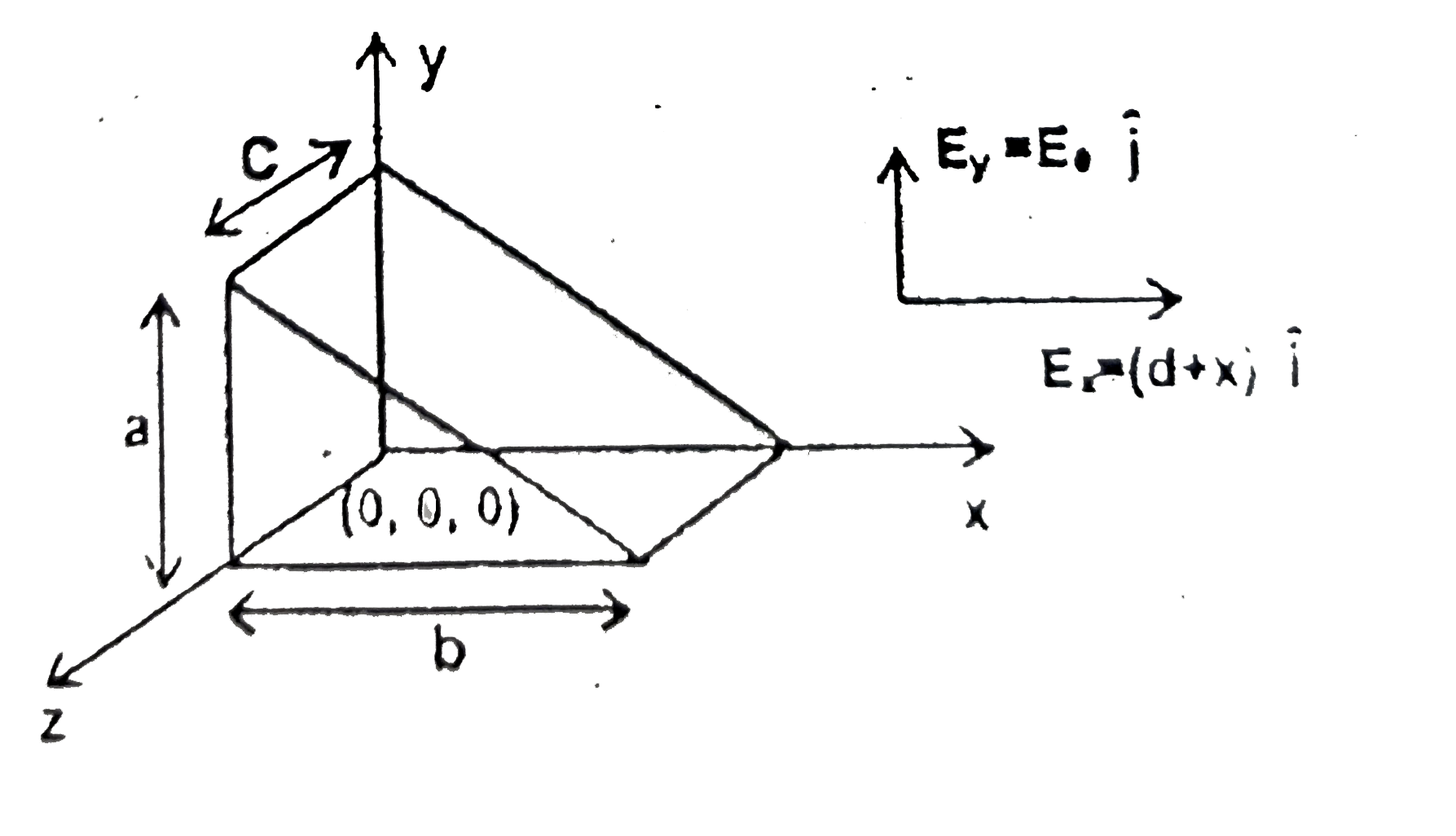
View SolutionAt each point on the surface of the cube shown in the figure, the electric field is parllel to the z- axis. The length of each edge of the cube is 3.0 m on the bottom face it is →E=34ˆkN/C and on the bottom face it is →E=20ˆkN/C . Find the net flux contained within the cube.
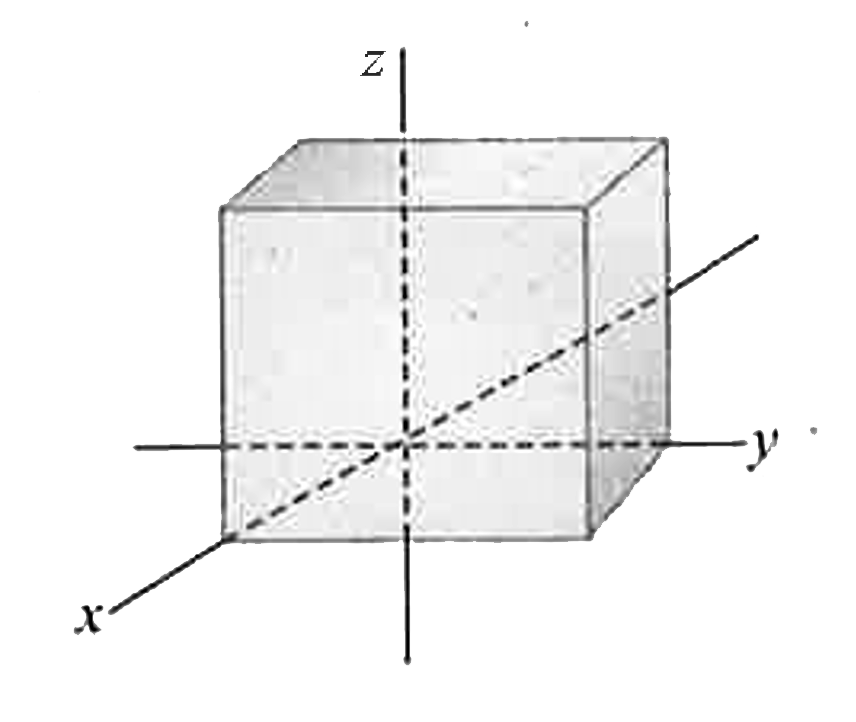
View SolutionAt each point on the surface of the cube shown in the figure, the electric field is parllel to the z- axis. The length of each edge of the cube is 3.0 m on the bottom face it is →E=34ˆkN/C and on the bottom face it is →E=20ˆkN/C . Find the net flux contained within the cube.

View SolutionThe centre of the circle passing through the points (0,0), (1,0) and touching the circle x2+y2=9 is
View Solution
