If a cavity is made as shown in the uniformaly charged sphere find the electric field at an arbitary point inside the cavity.

∫E=p→l3ε0
Topper's Solved these Questions
- GAUSS' LAW BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
20 Videos
- GAUSS' LAW BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
2 Videos
- GAUSS' LAW BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - CHECKPOINT
7 Videos
- FORCE AND MOTION-IIBOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
1 Videos
- GEOMETRICAL OPTICS : REFLECTION BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
Similar Questions
A sphere of radius R has a uniform volume density ρ. A spherical cavity of radius b, whose center lies at →a, is removed from the sphere.
i. Find the electric field at any point inside the spherical cavity.
ii. Find the electric field outside the cavity
(a) at points inside the large sphere but outside the cavity and
(b) at points outside the large sphere.

View SolutionA sphere of radius R has a uniform volume density ρ. A spherical cavity of radius b, whose center lies at →a, is removed from the sphere.
i. Find the electric field at any point inside the spherical cavity.
ii. Find the electric field outside the cavity
(a) at points inside the large sphere but outside the cavity and
(b) at points outside the large sphere.

View Solution
Knowledge Check
There is a uniformly charged non-conducting solid sphere. A spherical cavity is made whose centre does not coincide with the centre of solid sphere. Electric field intensity inside the cavity is
Adirectly proportional to distance of the point from centre of cavityBdirectly proportional to the distance of the point from centre of sphereCuniformDnot predictable due to insufficient information
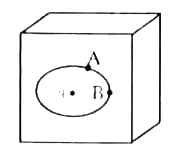
An ellipsoidal cavity is carved with in a perfect conductor. A positive charge q is placed at the centre of the cavity. The points A and B are on the cavity surface as shown in the figure then
(a) Electric field near A in the cavity = Electric field near B in the cavity
(b) Charge density at A= Charge density at B
(c ) Potential at A= Potential at B
(d) Total electric flux through the surface of the cavity is q/ε0.
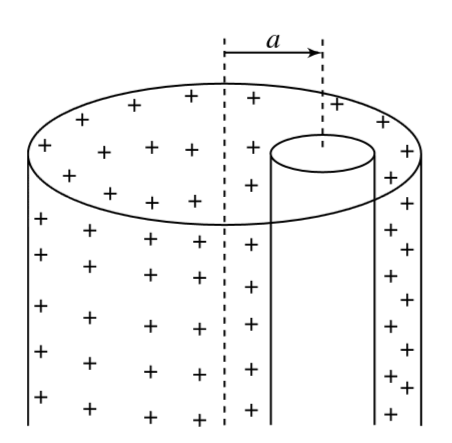
View Solution(a) There is a long uniformly charged cylinder having a volume charge density of ρC/m3. Radius of the cylinder is R. Find the electric field at a point at a distance x from the axis of the cylinder for following cases (i) x lt R (ii) x gt R What is the maximum field produced by the charge distribution at any point? (b) The cylinder described in (a) has a long cylindrical cavity. The axis of cylindrical cavity is at a distance a from the axis of the charged cylinder (see figure). Find electric field inside the cavity.
View SolutionPositive charge is uniformly distrubuted with volume charge density ρ of sphere of radius R. A spherical cavity is created in the sphere as shown in figure. This electric field intensity inside the cavity at point P is(where CP =R/5 , C0C = 2R/3 , radius of cavity is R/4, C0 & C are centre of sphere & cavity respectively)
View SolutionA solid sphere of radius 'R' has a cavity of radius R2. The solid part has a uniform charge density 'ρ' and cavity has no charge. Find the electric potential at point 'A'. Also find the electric field (only magnetude) at point 'C' inside the cavity
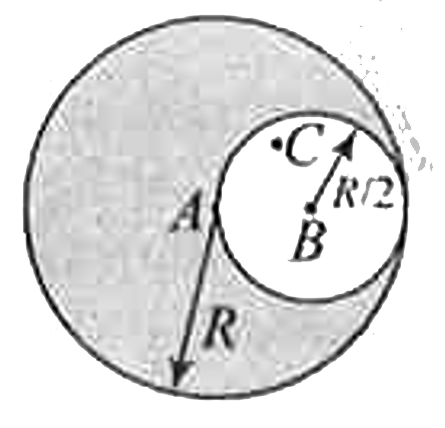
View SolutionA solid sphere of radius 'R' has a cavity of radius R2. The solid part has a uniform charge density 'ρ' and cavity has no charge. Find the electric potential at point 'A'. Also find the electric field (only magnitude) at point 'C' inside the cavity
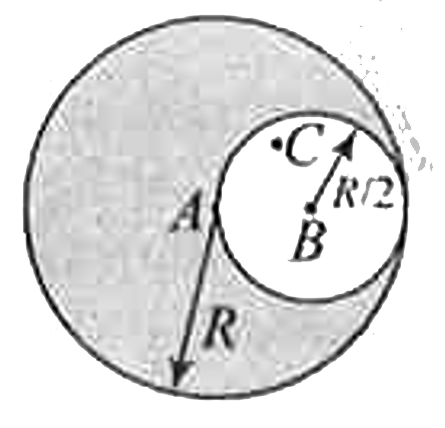
View SolutionA uniform solid of valume mass density ρ and radius R is shown in figure.
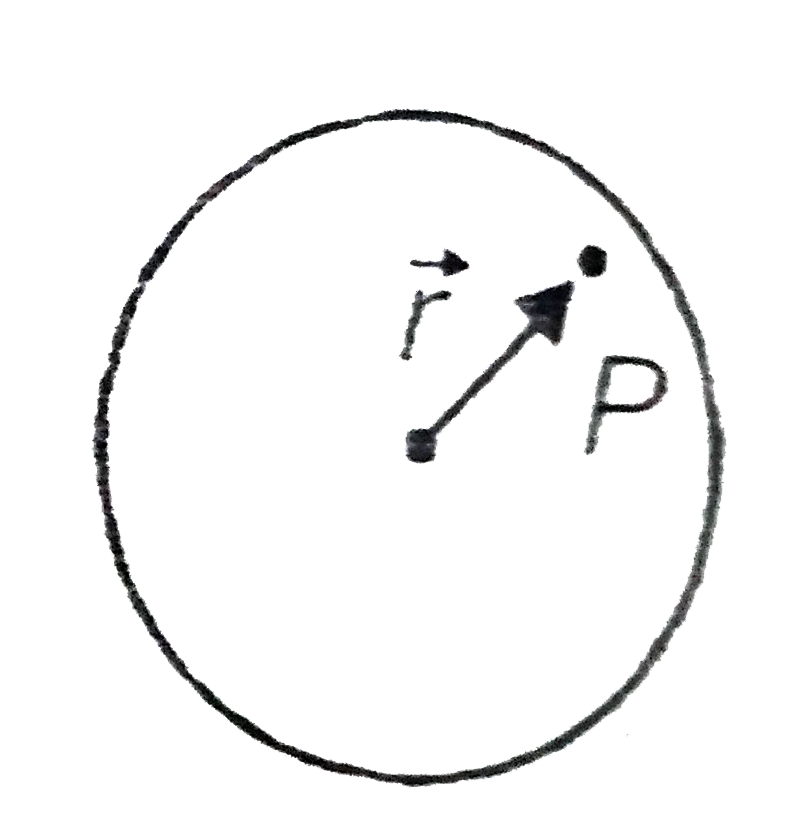
(a) Find the gravitational field at a point P inside the sphere at a distance r from the centre of the sphere. Represent the gravitational field vector →l in terms of radius vector →r of point P.
(b) Now a spherical cavity is made inside the solid sphere in such a way that the point P comes inside the cavity. The centre is at a distance a from the centre of solid sphere and point P is a distance of b from the centre of the cavity. Find the gravitational field →E at point P in vector formulationand interpret the result.
View SolutionThe distance between the centres of the Moon and the earth is D. The mass of the earth is 81 times the mass of the Moon. At what distance from the centre of the earth, the gravitational force will be zero?
View Solution
