It is desired to make a coil of wire, which has a zero thermal coefficient of resistance. To do this, a carbon resistor of resistance is placed in series with an iron resistor of resistance . The proportions of iron and carbon are so chosen that for all temperatures near How long are ?
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-1)
17 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)
16 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA
2 Videos
Similar Questions
It is desired to make a 20Ω coil of wire, which has a zero thermal coefficient of resistance. To do this, a carbon resitor fo resistane R1 is placed in series with an iron resistor of resistance R2 the proportions of iron and carbon are so chosen that R1+R2=20Ω for all temperatures near 20∘C. How long are R1andR2? αcarbon=−0.5×10−3.∘C−1,αiron=5×10−3.∘C(−1)
View SolutionA resistor of resistance R is connected to a cell internal resistance 5Ω. The value of R is varied from 1Ω to 5Ω. The power consumed by R
View Solution
Knowledge Check
It is desired to make a long cylindrical conductor whose temperature coefficient of resistivity at 20∘C will be close to zero. If such a conductor is made by assembling alternate disks of iron and carbon, find the ratio of the thickness of a carbon disk to that an iron disk. (For carbon,p=3500×10−8Ωmandα=−0.50×10−3.∘C−1for iron, p=9.68×10−8Ωmandα=6.5×10−3.∘C−1)
A0.36B0.036C1D2
The temperature coefficient of resistance of conductor varies as α(T)=3T2+2T. If R0 is resistance at T = 0and R is resistance at T, then
View SolutionA galvanometer has range 0 − V volt and it has resistance R. When the series resistor of resistance 2R is connected, the range becomes 0 ⋅ V . Then
View SolutionConsider the circuit shown in fig.
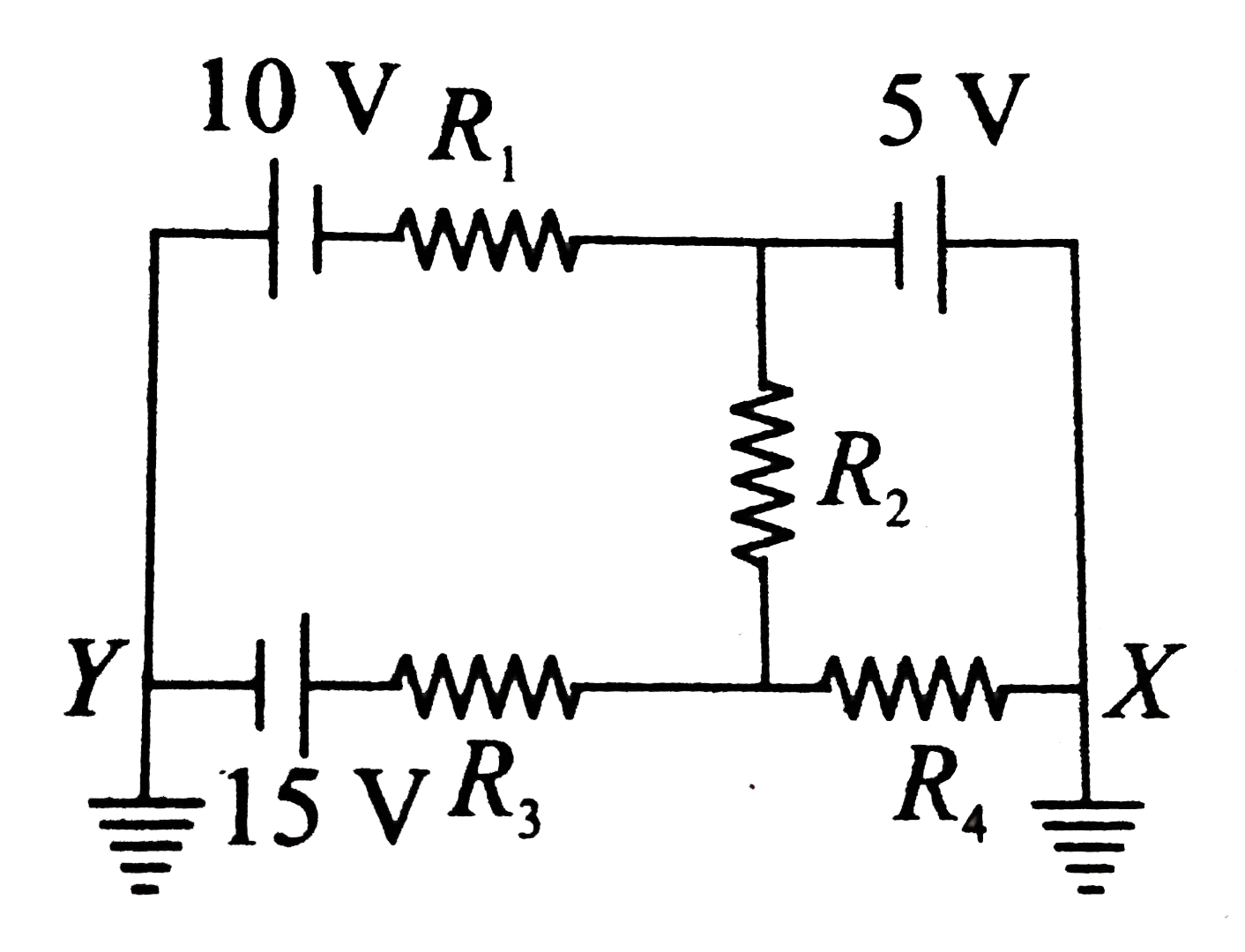
Assuming R1=2Ω, current passing through resistance R1 is
View SolutionTwo resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
View SolutionTwo resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
View SolutionShow by a diagram how two resistors R1andR2 are joined in parallel. Obtain an expression for the total resistance of the combination.
View SolutionA resistance R of therimal coefficient of resistivity α is connected in parallel with a resistance 3R. Having thermal coeffiecinet of resistivity 2α Find the value of αeff
View Solution
