A galvanometer has range 0 − V volt and it has resistance R. When the series resistor of resistance 2R is connected, the range becomes 0 ⋅ V . Then
To solve the problem, we need to analyze the behavior of the galvanometer when a series resistor is added. Let's break it down step by step.
Step 1: Understand the initial setup
The galvanometer has a voltage range of 0 to V volts and a resistance of R. This means that when the galvanometer is connected to a voltage source of V volts, it will allow a certain current (let's denote this current as Ig) to pass through it.
Step 2: Calculate the current through the galvanometer
Using Ohm's law, the voltage across the galvanometer can be expressed as:
V=Ig⋅R
This equation indicates that the current Ig flowing through the galvanometer when a voltage V is applied is given by:
Ig=VR
Step 3: Analyze the new setup with the series resistor
Now, when a series resistor of resistance 2R is connected, the total resistance in the circuit becomes R+2R=3R. The current through the circuit will now be different because of the increased total resistance.
Step 4: Calculate the new current
The new current I′ flowing through the circuit can be calculated using Ohm's law again:
V′=I′⋅(R+2R)=I′⋅3R
Where V′ is the new voltage that the galvanometer can measure. Rearranging gives:
I′=V′3R
Step 5: Relate the new current to the galvanometer's original current
Since the galvanometer measures the same current Ig as before, we can set I′=Ig:
V′3R=VR
Step 6: Solve for the new voltage range
Cross-multiplying gives:
V′=V⋅3RR=3V
This means that the new range of the galvanometer when the series resistor of resistance 2R is connected becomes 0 to 3V.
Conclusion
Thus, the new range of the galvanometer is 0 to 3V.
The galvanometer has a voltage range of 0 to V volts and a resistance of R. This means that when the galvanometer is connected to a voltage source of V volts, it will allow a certain current (let's denote this current as Ig) to pass through it.
Using Ohm's law, the voltage across the galvanometer can be expressed as:
V=Ig⋅R
This equation indicates that the current Ig flowing through the galvanometer when a voltage V is applied is given by:
Ig=VR
Now, when a series resistor of resistance 2R is connected, the total resistance in the circuit becomes R+2R=3R. The current through the circuit will now be different because of the increased total resistance.
The new current I′ flowing through the circuit can be calculated using Ohm's law again:
V′=I′⋅(R+2R)=I′⋅3R
Where V′ is the new voltage that the galvanometer can measure. Rearranging gives:
I′=V′3R
Since the galvanometer measures the same current Ig as before, we can set I′=Ig:
V′3R=VR
Cross-multiplying gives:
V′=V⋅3RR=3V
This means that the new range of the galvanometer when the series resistor of resistance 2R is connected becomes 0 to 3V.
Thus, the new range of the galvanometer is 0 to 3V.
Similar Questions
A voltmeter has a range O−V with a series resistance R. With a series resistance 2R, the range is O−V'. The correct relation between V and V'is
View SolutionA 100V voltmeter of internal resistance 20kΩ in series with a high resistance R is connected to a 110V line. The voltmeter reads 5V, the value of R is
View Solution
Knowledge Check
- Question 1 - Select One
When a resistance of 100Ω is connected in series with a galvanometer of resistance R, then its range is V. To double its range, a resistance of 1000Ω is connected in series. Find the value of R.
A1100B1000C900D800
A 1Ω voltmeter has range 1V find the additional resistance which has to join in series in voltmeter to increase the range of voltmeter to 100V :-
View SolutionA galvanmeter of resistance G is converted into a voltmeter of range 0 -1V by connecting resistance R1 in series with it. The additional resistance that should be connected in series with R1 to increase the range of the voltmeter to 0-2 V will be :
View SolutionA voltmeter has a resistance G and range V. Calculate the resistance to be used in series with it to extend its range to nV.
View SolutionA voltmeter has a resistance G and range V. Calculate the resistance to be used in series with it to extend its range to nV.
View SolutionIn the circuit shows in Fig. 6.42, resistors X and Y, each with resistance R, are connected to a 6V battery of negligible internal resistance. A voltmeter, also of resistance R, is connected across Y.
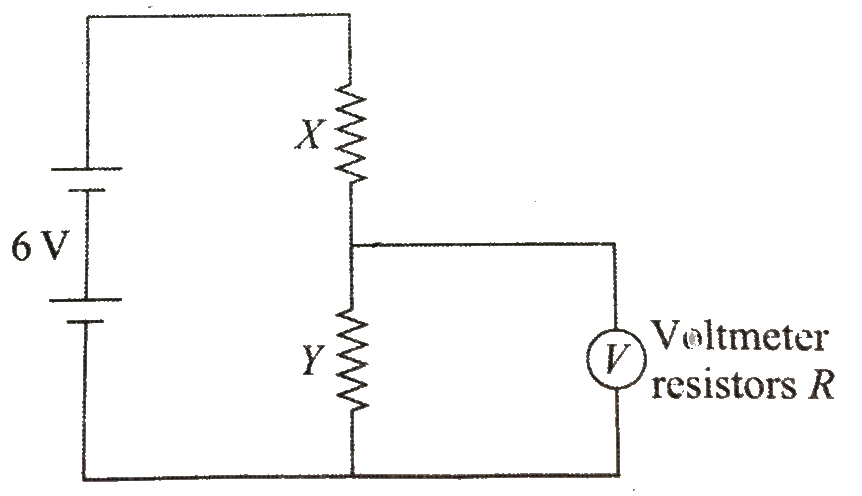
What is the reading of the voltmeter?View SolutionWhen a resistance of 100Ω is connected in series with a galvanometer of resistance R, then its range is V. To double its range, a resistance of 1000Ω is connected in series. Find the value of R.
View SolutionAn ammeter has resistance R0 and range l what resistance should be connected in parallel with it to increase its range by nl ?
View Solution

