Let A_(0) be the area enclined by the orbit in a hydrogen atom .The graph of in (A0/A1) againest in(pi)
will pass through the origin
will be a straigth line with slope 4
will be a monotonically increasing nonlinear curve
will be a circle
The correct Answer is:A, B
To solve the problem step by step, we will analyze the area of the orbits in a hydrogen atom according to Bohr's model and how it relates to the logarithmic graph of A0A1 against log(n).
Step 1: Understand the radius of the nth orbit
According to Bohr's model, the radius Rn of the nth orbit in a hydrogen atom is given by:
Rn=n2a0
where a0 is the Bohr radius.
Step 2: Calculate the area of the nth orbit
The area An of the nth orbit (which is circular) can be calculated using the formula for the area of a circle:
An=πR2n
Substituting the expression for Rn:
An=π(n2a0)2=πn4a20
Step 3: Calculate the area of the first orbit
For the first orbit (where n=1):
A1=π(12a0)2=πa20
Step 4: Formulate the ratio of areas
Now, we can find the ratio of the area of the nth orbit to the area of the first orbit:
AnA1=πn4a20πa20=n4
Step 5: Take the logarithm of the ratio
Taking the logarithm of both sides gives:
log(AnA1)=log(n4)
Using the properties of logarithms, we can simplify this to:
log(AnA1)=4log(n)
Step 6: Analyze the relationship
This shows that log(AnA1) is directly proportional to log(n). Thus, we can express this relationship as:
log(AnA1)=4log(n)
Step 7: Graphical representation
When we plot log(AnA1) on the y-axis against log(n) on the x-axis, we will get a straight line passing through the origin with a slope of 4.
Conclusion
Thus, the graph of log(A0A1) against log(n) will be a straight line with a slope of 4.
According to Bohr's model, the radius Rn of the nth orbit in a hydrogen atom is given by:
Rn=n2a0
where a0 is the Bohr radius.
The area An of the nth orbit (which is circular) can be calculated using the formula for the area of a circle:
An=πR2n
Substituting the expression for Rn:
An=π(n2a0)2=πn4a20
For the first orbit (where n=1):
A1=π(12a0)2=πa20
Now, we can find the ratio of the area of the nth orbit to the area of the first orbit:
AnA1=πn4a20πa20=n4
Taking the logarithm of both sides gives:
log(AnA1)=log(n4)
Using the properties of logarithms, we can simplify this to:
log(AnA1)=4log(n)
This shows that log(AnA1) is directly proportional to log(n). Thus, we can express this relationship as:
log(AnA1)=4log(n)
When we plot log(AnA1) on the y-axis against log(n) on the x-axis, we will get a straight line passing through the origin with a slope of 4.
Thus, the graph of log(A0A1) against log(n) will be a straight line with a slope of 4.
Topper's Solved these Questions
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Exercises
46 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Obejective - I
13 Videos
- ALTERNATING CURRENTBOOK - HC VERMA ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Short answer
14 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer
7 Videos
Similar Questions
Let A0 be the area enclined by the orbit in a hydrogen atom .The graph of in (A0/A1) against ln(n)
View SolutionLet An be the area enclosed by the nth orbit in a hydrogen atom. The graph of ln(An/At) against In (n)
View SolutionThe figure shows a graph between 1n∣∣∣AnA1∣∣∣ and 1n|n|, where An is the area enclosed by the nth orbit in a hydrogen like atom. The correct curve is
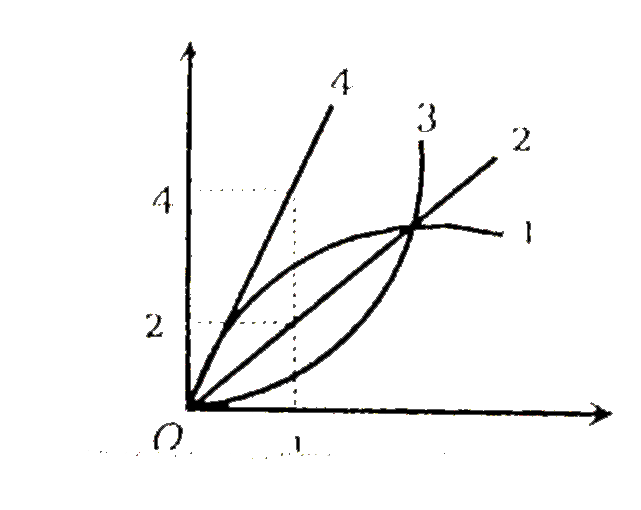
View SolutionThe figure shows a graph between 1n∣∣∣AnA1∣∣∣ and 1n|n|, where An is the area enclosed by the nth orbit in a hydrogen like atom. The correct curve is
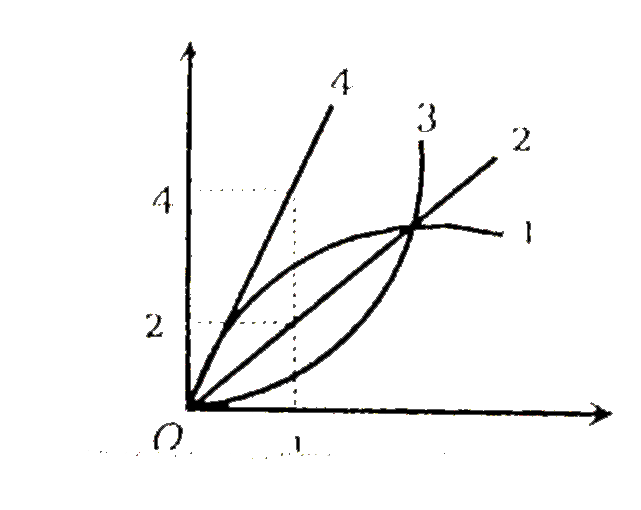
View SolutionIn terms of Bohr radius a0, the radius of the second Bohr orbit of a hydrogen atom is given by
View SolutionThe kinetic energy of the electron in the second Bohr's orbit of a hydrogen atom [a0 is Bohr's radius] is
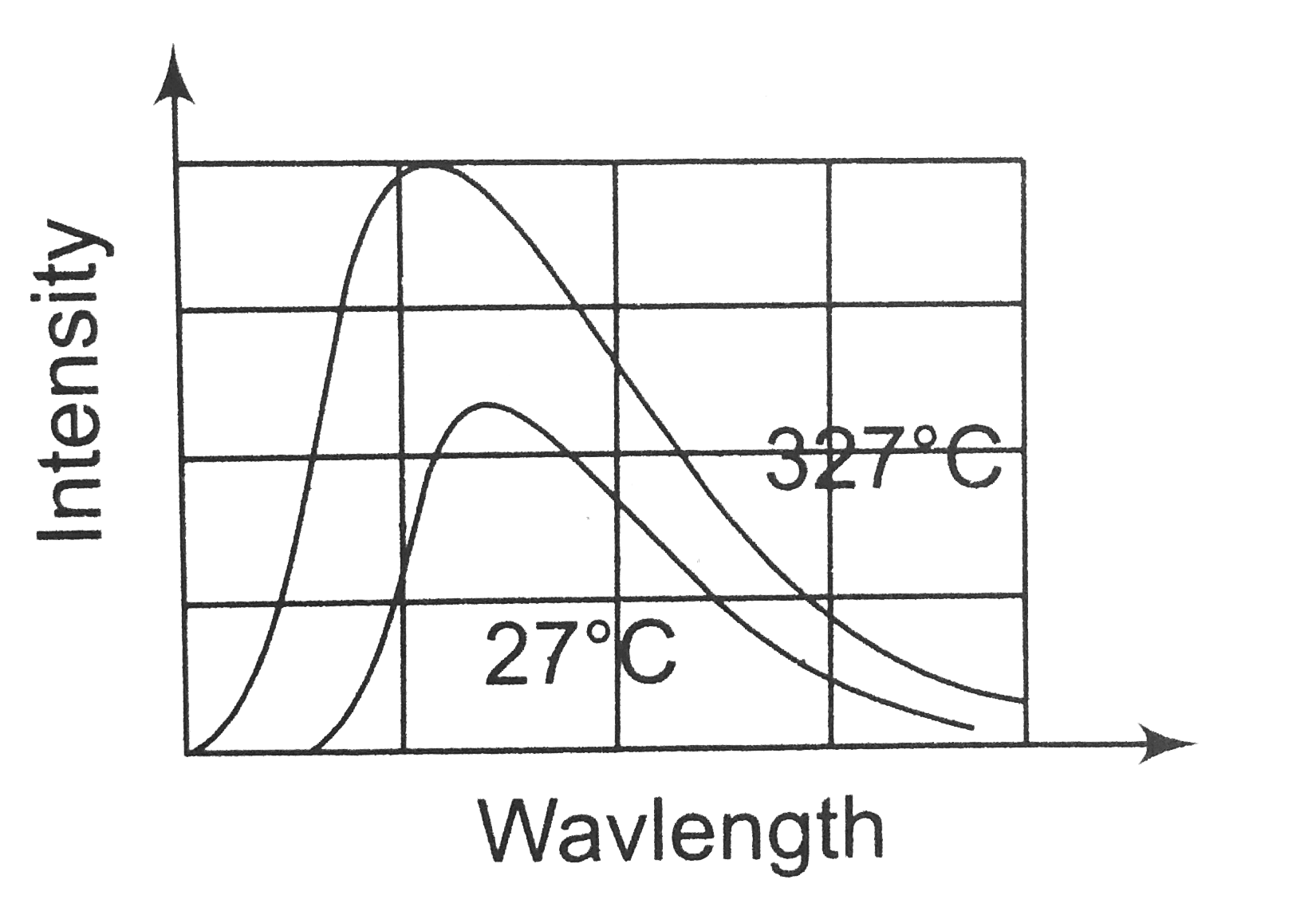
View SolutionThe spectrum of a black body at two temperatures 27∘C and 327∘C is shown in the figure. Let A1 and A2 be the areas under the two curves respectively. Find the value of A2A1
View SolutionLet A (a,b) be a fixed point and O be the origin of coordionates. If A1 is the mid-point of OA, A2 is the mid- poind of AA1,A3 is the mid-point of AA2 and so on. Then the coordinates of An are
View SolutionWhich one of the following about an electron occupying the 1s orbital in a hydrogen atom is incorrect ? (The Bohr radius is represented by a0).
View SolutionWhich one of the following about an electron occupying the 1s orbital in a hydrogen atom is incorrect ? (The Bohr radius is represented by a0).
View Solution
