Let A0 be the area enclined by the orbit in a hydrogen atom .The graph of in (A0/A1) against ln(n)
Will not pass through origin
Will be a straight line with slope 4
will be rectangular hyperbola
Will be parabola
The correct Answer is:B
To solve the problem step by step, we need to analyze the relationship between the areas of the orbits in a hydrogen atom and the principal quantum number n.
Step 1: Understand the relationship between radius and quantum number
The radius of the nth orbit in a hydrogen atom is given by:
rn=n2r1
where r1 is the radius of the first orbit.
Step 2: Calculate the area of the orbits
The area An of the nth orbit can be calculated using the formula for the area of a circle:
An=πr2n
Substituting the expression for rn:
An=π(n2r1)2=πn4r21
Step 3: Express the area of the first orbit
The area of the first orbit A1 is:
A1=πr21
Step 4: Find the ratio of the areas
Now, we can find the ratio of the area of the nth orbit to the area of the first orbit:
AnA1=πn4r21πr21=n4
Step 5: Take the natural logarithm of the ratio
Taking the natural logarithm of both sides gives:
ln(AnA1)=ln(n4)=4ln(n)
Step 6: Graph the relationship
The equation ln(AnA1)=4ln(n) indicates that if we plot ln(AnA1) against ln(n), we will get a straight line with a slope of 4.
Conclusion
Thus, the graph of A0A1 against ln(n) will be a straight line with a slope of 4.
The radius of the nth orbit in a hydrogen atom is given by:
rn=n2r1
where r1 is the radius of the first orbit.
The area An of the nth orbit can be calculated using the formula for the area of a circle:
An=πr2n
Substituting the expression for rn:
An=π(n2r1)2=πn4r21
The area of the first orbit A1 is:
A1=πr21
Now, we can find the ratio of the area of the nth orbit to the area of the first orbit:
AnA1=πn4r21πr21=n4
Taking the natural logarithm of both sides gives:
ln(AnA1)=ln(n4)=4ln(n)
The equation ln(AnA1)=4ln(n) indicates that if we plot ln(AnA1) against ln(n), we will get a straight line with a slope of 4.
Thus, the graph of A0A1 against ln(n) will be a straight line with a slope of 4.
Topper's Solved these Questions
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 More Than One Correct
6 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Comprehension Based
3 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 1 Subjective
40 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MODERN PHYSICS - 2BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 Subjective
10 Videos
Similar Questions
Let A_(0) be the area enclined by the orbit in a hydrogen atom .The graph of in (A0/A1) againest in(pi)
View SolutionLet An be the area enclosed by the nth orbit in a hydrogen atom. The graph of ln(An/At) against In (n)
View SolutionThe figure shows a graph between 1n∣∣∣AnA1∣∣∣ and 1n|n|, where An is the area enclosed by the nth orbit in a hydrogen like atom. The correct curve is
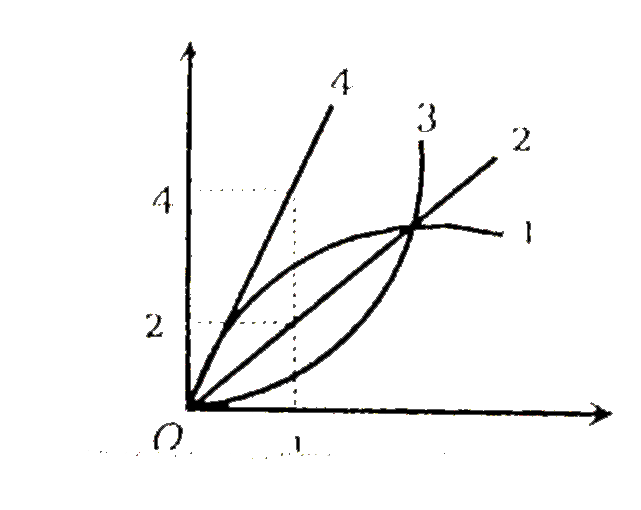
View SolutionThe figure shows a graph between 1n∣∣∣AnA1∣∣∣ and 1n|n|, where An is the area enclosed by the nth orbit in a hydrogen like atom. The correct curve is
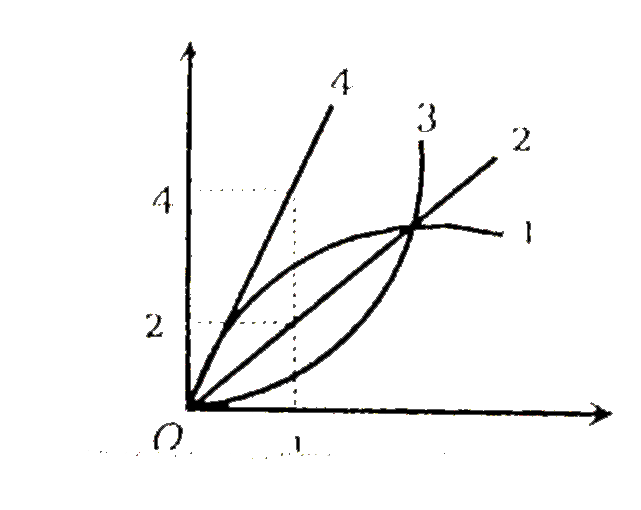
View SolutionLet A (a,b) be a fixed point and O be the origin of coordionates. If A1 is the mid-point of OA, A2 is the mid- poind of AA1,A3 is the mid-point of AA2 and so on. Then the coordinates of An are
View SolutionIf, in a hydrogen atom, radius of nth Bohr orbit is rn frequency of revolution of electron in nth orbit is fn and area enclosed by the nth orbit is An , then which of the pollowing graphs are correct?
View SolutionLet Ar be the area of the region bounded between the curves y2=(e−kr)x(where k>0,r∈N) and the line y=mx(where m≠0), k and m are some constants
A1,A2,A3,… are in G.P. with common ratio
View SolutionLet A=⎡⎢⎣1111−1001−1⎤⎥⎦,A1 be a matrix formed by the cofactors of the elements of the matrix A and A2 be a matrix formed by the cofactors of the elements of matrix A1. Similarly, If A10 be a matrrix formed by the cofactors of the elements of matrix A9, then the value of |A10| is
View SolutionLet A1,A2,A3,…..,An be squares such that for each n≥1 the length of a side of An equals the length of a diagonal of An+1. If the side of A1 be 20 units then the smallest value of 'n' for which area of An is less than 1.
View SolutionThe height of a plant is under the control of polygenic inheritance. The genotype of a plant A1A1A0A0 has 56 cm and the height of plant a1a1a0a0 is 26 cm. what is the contribution, of each polygene?
View Solution
