Let the angle between two non - zero vectors →A and →B be 120∘and its resultant be →C.
C must be equal to ∣∣→A−→B∣∣
C must be less than ∣∣→A−→B∣∣
C must be greater than ∣∣→A−→B∣∣
C may be equal to ∣∣→A−→B∣∣
The correct Answer is:B
To solve the problem regarding the resultant of two non-zero vectors →A and →B with an angle of 120∘ between them, we can follow these steps:
1. Identify the Given Information:
- Let the magnitudes of the vectors be A (for →A) and B (for →B).
- The angle θ between the vectors is 120∘.
2. Use the Formula for the Magnitude of the Resultant:
The magnitude of the resultant vector →C can be calculated using the formula:
|→C|=√A2+B2+2ABcos(θ)
3. Substitute the Values:
- Substitute θ=120∘ into the formula. We know that cos(120∘)=−12.
|→C|=√A2+B2+2AB(−12)
4. Simplify the Expression:
- This simplifies to:
|→C|=√A2+B2−AB
5. Analyze the Resultant Magnitude:
- We can analyze the relationship between the magnitudes of the vectors and the resultant:
|→C|=√A2+B2−AB
- We can also derive inequalities based on the triangle inequality theorem. The resultant |→C| must satisfy:
|→C|>|A−B|
- This means that the magnitude of the resultant vector is always greater than the absolute difference of the magnitudes of the two vectors.
Conclusion:
Thus, we conclude that the magnitude of the resultant vector |→C| is given by:
|→C|=√A2+B2−AB
- Let the magnitudes of the vectors be A (for →A) and B (for →B).
- The angle θ between the vectors is 120∘.
The magnitude of the resultant vector →C can be calculated using the formula:
|→C|=√A2+B2+2ABcos(θ)
- Substitute θ=120∘ into the formula. We know that cos(120∘)=−12.
|→C|=√A2+B2+2AB(−12)
- This simplifies to:
|→C|=√A2+B2−AB
- We can analyze the relationship between the magnitudes of the vectors and the resultant:
|→C|=√A2+B2−AB
- We can also derive inequalities based on the triangle inequality theorem. The resultant |→C| must satisfy:
|→C|>|A−B|
- This means that the magnitude of the resultant vector is always greater than the absolute difference of the magnitudes of the two vectors.
Thus, we conclude that the magnitude of the resultant vector |→C| is given by:
|→C|=√A2+B2−AB
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the angle between two vectors →a and →b is zero, then :
A→a.→b=|→a|∣∣→b∣∣B→a.→b=0C|→a|∣∣→b∣∣=1DNone of the aboveThe angle between two vector A and B is θ. Vector R is the resultant of the two vectors. If R makes an angle θ2 with A, then
AA=2BBA=B/2CA=BDAB=1If →A+→B=→C and the angle between →A and →B is 120∘, then the magnitude of →C
Amust be equal to ∣∣→A−→B∣∣Bmust be less than ∣∣→A−→B∣∣Cmust be greater than ∣∣→A−→B∣∣Dmust be equal to ∣∣→A−→B∣∣
Show that |→a|→b−∣∣→b∣∣→a, for any two non - zero vectors →a and →b.
View SolutionLet →a,→b,→c are three non-zero vectors and →b is neither perpendicular to →a nor to →c and "(→a×→b)×→c=→a×(→b×→c) .Then the angle between →a and →c is:
View SolutionLet →a,→b,→c be three non-zero vectors such that →c is a unit vector perpendicular to both →aand→b . If the between →aand→b is π/6 , prove that [→a→b→c]2=14|→a|2∣∣→b∣∣2.
View SolutionIf a vector →a is perpendicular to two non-collinear vector →b and →c , then →a is perpendicular to every vector in the plane of →b and →c .
View SolutionKeeping one vector constant, if direction of other to be added in the first vector is changed continuously, tip of the resultant vector describes a circles, In the following figure vector →a is kept constant. When vector →b addede to →a changes its direction, the tip of the resultant vector →r=→a+→b describes circles of radius b with its centre at the tip of vector →a. Maximum angle between vector →a and the resultant →r=→a+→b is
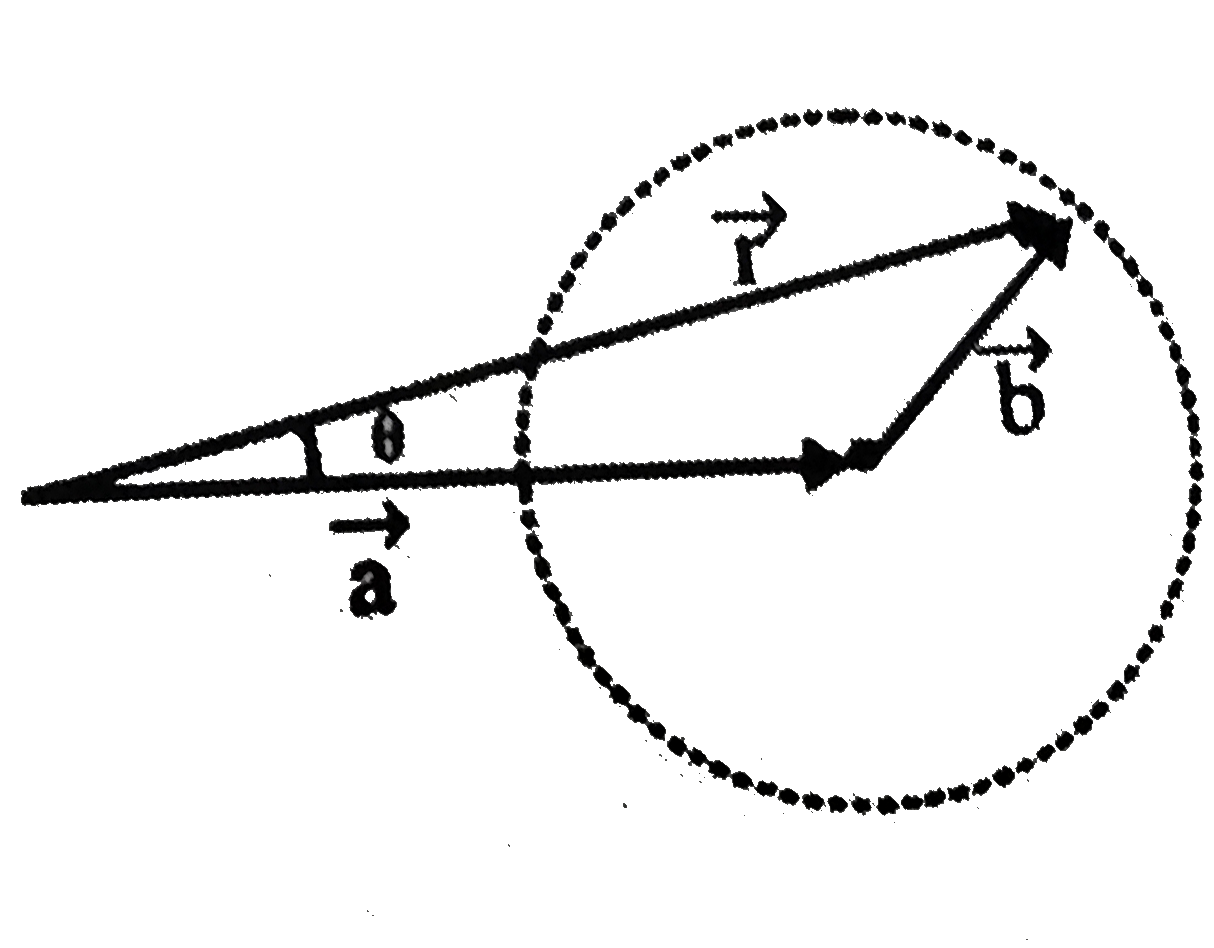
View Solution
