Locus of all the points in a plane on which the moment of inertia about all mutually parallel axes of a rigid body is same throughout is
a straight line
a circle
a parabola
an ellipse
The correct Answer is:B
To determine the locus of all points in a plane where the moment of inertia about all mutually parallel axes of a rigid body is the same, we can follow these steps:
Step 1: Understand the Moment of Inertia
The moment of inertia I of a rigid body about an axis is defined as:
I=∑mir2i
where mi is the mass of the individual particles and ri is the distance from the axis of rotation.
Step 2: Apply the Parallel Axis Theorem
According to the parallel axis theorem, the moment of inertia about a parallel axis can be expressed as:
I=Icm+Mh2
where:
- Icm is the moment of inertia about the center of mass,
- M is the total mass of the body,
- h is the distance between the two parallel axes.
Step 3: Analyze the Condition for Constant Moment of Inertia
For the moment of inertia to remain constant for all parallel axes, the term Mh2 must not change with different positions of the axis. This implies that the distance h must be constant.
Step 4: Determine the Locus of Points
If h is constant, then the locus of points that maintain this constant distance from a fixed point (the center of mass) forms a circle. This is because all points on a circle are equidistant from the center.
Conclusion
Thus, the locus of all points in a plane where the moment of inertia about all mutually parallel axes of a rigid body is the same is a circle.
Final Answer
The correct option is a circle.
---
The moment of inertia I of a rigid body about an axis is defined as:
I=∑mir2i
where mi is the mass of the individual particles and ri is the distance from the axis of rotation.
According to the parallel axis theorem, the moment of inertia about a parallel axis can be expressed as:
I=Icm+Mh2
where:
- Icm is the moment of inertia about the center of mass,
- M is the total mass of the body,
- h is the distance between the two parallel axes.
For the moment of inertia to remain constant for all parallel axes, the term Mh2 must not change with different positions of the axis. This implies that the distance h must be constant.
If h is constant, then the locus of points that maintain this constant distance from a fixed point (the center of mass) forms a circle. This is because all points on a circle are equidistant from the center.
Thus, the locus of all points in a plane where the moment of inertia about all mutually parallel axes of a rigid body is the same is a circle.
The correct option is a circle.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct
86 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
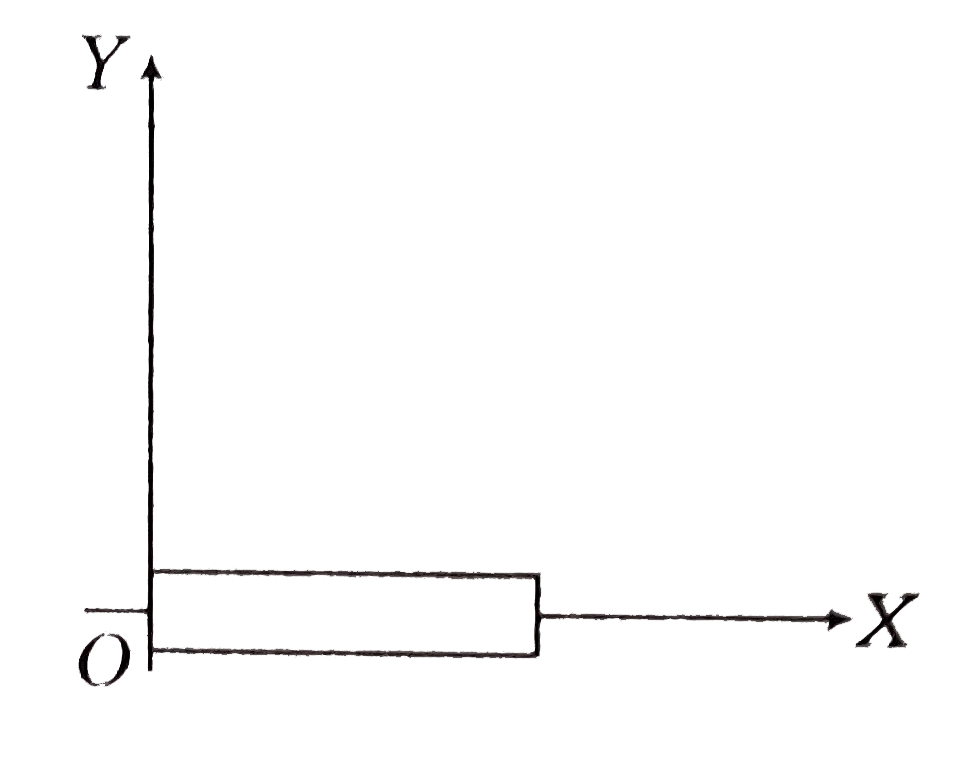
The figure shows a uniform rod lying along the X-axis. The locus of all the points lying on the XY-plane, about which the moment of inertia of the rod is same as that about O is
View SolutionAssertion : If we draw a circle around the centre of mass of a rigid body, then moment of inertia about all parallel axes passing through any point on this circle has a constant value.
Reason : Dimensions of radius gyration are [M0LT0]
View SolutionThe moment of inertia of a body about a given axis of rotation depends upon :-
View SolutionFour particle of mass m each are placed at four corners of a square ABCD of side a. Point O is the centre of the square. Moment of inertia of all four particles about an axis passing through
View SolutionCalculate the moment of inertia of a ring about a tangent to the circle of the ring normal to its plane.
View SolutionCalculate the moment of inertia of a ring about a tangent to the circle of the ring normal to its plane.
View SolutionMoment of inertia of a uniform circular disc about a diameter is I. Its moment of inertia about an axis perpendicular to its plane and passing through a point on its rim will be.
View SolutionOne circular ring and one circular disc, both are having the same mass and radius. The ratio of their moments of inertia about the axes passing through their centres and perpendicular to their planes, will be
View SolutionThe mass of a body cannot be considered to be concentrated at the centre of mass of the body for the purpose of computing its moment of inertia.
For then the moment of inertia of every body about an axis passing through its centre of mass would be zero.
View SolutionAll fluorine atoms are in same plane in
View Solution
