Magnetic field at the centre of a circualr loop of area A carrying current I is B. What is the magnetic moment of this loop?
The correct Answer is:D
To find the magnetic moment M of a circular loop of area A carrying a current I that produces a magnetic field B at its center, we can follow these steps:
Step 1: Understand the relationship between magnetic field and current
The magnetic field B at the center of a circular loop is given by the formula:
B=μ0I2R
where μ0 is the permeability of free space and R is the radius of the loop.
Step 2: Relate area and radius
The area A of the circular loop is given by:
A=πR2
From this, we can express the radius R in terms of the area A:
R=√Aπ
Step 3: Substitute R into the magnetic field equation
Substituting the expression for R into the magnetic field equation gives:
B=μ0I2√Aπ
This can be rearranged to find the current I:
I=2B√Aπμ0
Step 4: Use the formula for magnetic moment
The magnetic moment M of the loop is given by:
M=I⋅A
Substituting the expression for I from the previous step into this equation:
M=⎛⎜
⎜⎝2B√Aπμ0⎞⎟
⎟⎠⋅A
Step 5: Simplify the expression for magnetic moment
Now, simplifying the expression:
M=2BA√Aπμ0
This can be rewritten as:
M=2BAμ0⋅√Aπ
Final Result
Thus, the magnetic moment M of the loop is:
M=2BAμ0⋅√Aπ
The magnetic field B at the center of a circular loop is given by the formula:
B=μ0I2R
where μ0 is the permeability of free space and R is the radius of the loop.
The area A of the circular loop is given by:
A=πR2
From this, we can express the radius R in terms of the area A:
R=√Aπ
Substituting the expression for R into the magnetic field equation gives:
B=μ0I2√Aπ
This can be rearranged to find the current I:
I=2B√Aπμ0
The magnetic moment M of the loop is given by:
M=I⋅A
Substituting the expression for I from the previous step into this equation:
M=⎛⎜
⎜⎝2B√Aπμ0⎞⎟
⎟⎠⋅A
Now, simplifying the expression:
M=2BA√Aπμ0
This can be rewritten as:
M=2BAμ0⋅√Aπ
Thus, the magnetic moment M of the loop is:
M=2BAμ0⋅√Aπ
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - HOTS
5 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXEMPLAR PROBLEMS
6 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason
15 Videos
Similar Questions
The magnetic field at the centre of an equilateral triangular loop of side 2L and carrying a current i is
View SolutionThe diagram below shows a loop of wire carrying current I:

What is the magnetic polarity of the loop that faces us?
View SolutionIF B is the magnetic field at the centre of a circular loop of area A and its magnetic dipole moment is found to be nBAmμ0√π, then what is the value of n+m?
View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionFind the magnetic field B at the centre of a rectangular loop of length l and width b, carrying a current i.
View SolutionMagnetic field at the centre of regular hexagon current carrying loop of side length l and current i is
View SolutionA circular loop carrying a current is replaced by an equivalent magnetic dipole. A point on the axis of the loop is in
View SolutionThe magnetic field Intensity at the point o of a loop carrying current i as shown in the figure is
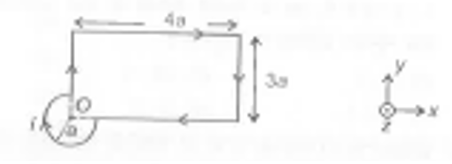
View SolutionA very long bar magnet is placed with its north pole coinciding with the centre of a circular loop carrying an electric current. i. The magnetic field due to the magnet at a point on the periphery of the wire is B. The radius of the loop is a. The force on the wire is
View SolutionAssertion : A planar circular loop of area A and carrying current I is equivalent to magnetic dipole of dipole moment M = IA.
Reason : At large distances, magnetic field of circular loop and magnetic dipole is same.
View Solution
