Magnetic field at the centre of a circualr loop of area A carrying current I is B. What is the magnetic moment of this loop?
BA2μ0π
BAμ0√A
2BA√A√πμ0
2BAμ0√Aπ
The correct Answer is:D
To find the magnetic moment of a circular loop carrying current, we can follow these steps:
Step 1: Understand the relationship between magnetic field and current
The magnetic field B at the center of a circular loop of radius R carrying current I is given by the formula:
B=μ0I2R
where μ0 is the permeability of free space.
Step 2: Relate area and radius
The area A of the circular loop is given by:
A=πR2
From this, we can express the radius R in terms of the area A:
R=√Aπ
Step 3: Substitute R into the magnetic field equation
Substituting the expression for R into the magnetic field equation, we have:
B=μ0I2√Aπ
This simplifies to:
B=μ0I√π2√A
Step 4: Solve for current I
Rearranging the equation to solve for I:
I=2B√Aμ0√π
Step 5: Calculate the magnetic moment
The magnetic moment M of the loop is given by the product of the current I and the area A:
M=I⋅A
Substituting the expression for I:
M=(2B√Aμ0√π)⋅A
This simplifies to:
M=2BA√Aμ0√π
Final Answer
Thus, the magnetic moment M of the circular loop is:
M=2BA√Aμ0√π
The magnetic field B at the center of a circular loop of radius R carrying current I is given by the formula:
B=μ0I2R
where μ0 is the permeability of free space.
The area A of the circular loop is given by:
A=πR2
From this, we can express the radius R in terms of the area A:
R=√Aπ
Substituting the expression for R into the magnetic field equation, we have:
B=μ0I2√Aπ
This simplifies to:
B=μ0I√π2√A
Rearranging the equation to solve for I:
I=2B√Aμ0√π
The magnetic moment M of the loop is given by the product of the current I and the area A:
M=I⋅A
Substituting the expression for I:
M=(2B√Aμ0√π)⋅A
This simplifies to:
M=2BA√Aμ0√π
Thus, the magnetic moment M of the circular loop is:
M=2BA√Aμ0√π
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Only One Option is Correct
45 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - More than One Option is Correct
25 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
Similar Questions
The magnetic field at the centre of an equilateral triangular loop of side 2L and carrying a current i is
View SolutionThe diagram below shows a loop of wire carrying current I:
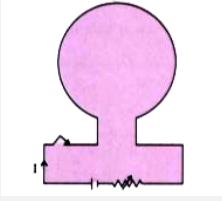
What is the magnetic polarity of the loop that faces us?
View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionFind the magnetic field B at the centre of a rectangular loop of length l and width b, carrying a current i.
View SolutionMagnetic field at the centre of regular hexagon current carrying loop of side length l and current i is
View SolutionA circular loop carrying a current is replaced by an equivalent magnetic dipole. A point on the axis of the loop is in
View SolutionThe magnetic field Intensity at the point o of a loop carrying current i as shown in the figure is
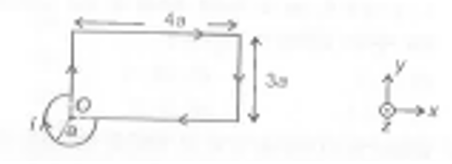
View SolutionA very long bar magnet is placed with its north pole coinciding with the centre of a circular loop carrying an electric current. i. The magnetic field due to the magnet at a point on the periphery of the wire is B. The radius of the loop is a. The force on the wire is
View SolutionAssertion : A planar circular loop of area A and carrying current I is equivalent to magnetic dipole of dipole moment M = IA.
Reason : At large distances, magnetic field of circular loop and magnetic dipole is same.
View SolutionThe radius of a circular loop is r and a current i is flowing in it. The equivalent magnetic moment will be
View Solution
