Make sure that the current distribution over two resistances R1 and R2 connnected in parallel corresponds to the minimum thermal power generated in this circuit.
Video Solution
Text Solution
We assume current conservation but not Kithoff's secound law. Then thermal power dissipated is
P(i1)=i21R1+(i−i1)2R2
=i21(R1+R2)−2ii1R2+i2R2
=[R1+R2][i1−R2R1+R2i]2+i2R1R2R1+R2
The resistances being positive we see that the power dissipated is minimum when
i2=iR2R1+R2
This correponds to usual distribution of currents over resistance joined is parallel.

|
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Constant Magnetic Fiels - Magnetics
69 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction
84 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field
46 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
Knowledge Check
Two wires with resistances R and 2 R are connected in parallel, the ratio of heat generated in 2 R and R is
A1:2B2:1C1:4D4:1Two resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
AR>R1+R2BR1<R<R2CR2<R<(R1+R2)DR<R1Two resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
AR>R1+R2BR1<R<R2CR2<R<(R1+R2)DR<R1
A cell develops the same power across two resistances R1 and R2 separately. The internal resistance of the cell is
View SolutionIn the circuit shown in the given figure, the resistances R1andR2 are respectively

View Solution
A dc source with internal resistance R0 is loaded with three identical resistance R as shown in the figure. At what value of R will the thermal power generated in this circuit be the highest?
View SolutionIn the given circuit, the valuue of R so that thermal power generated in R will be maximum is:
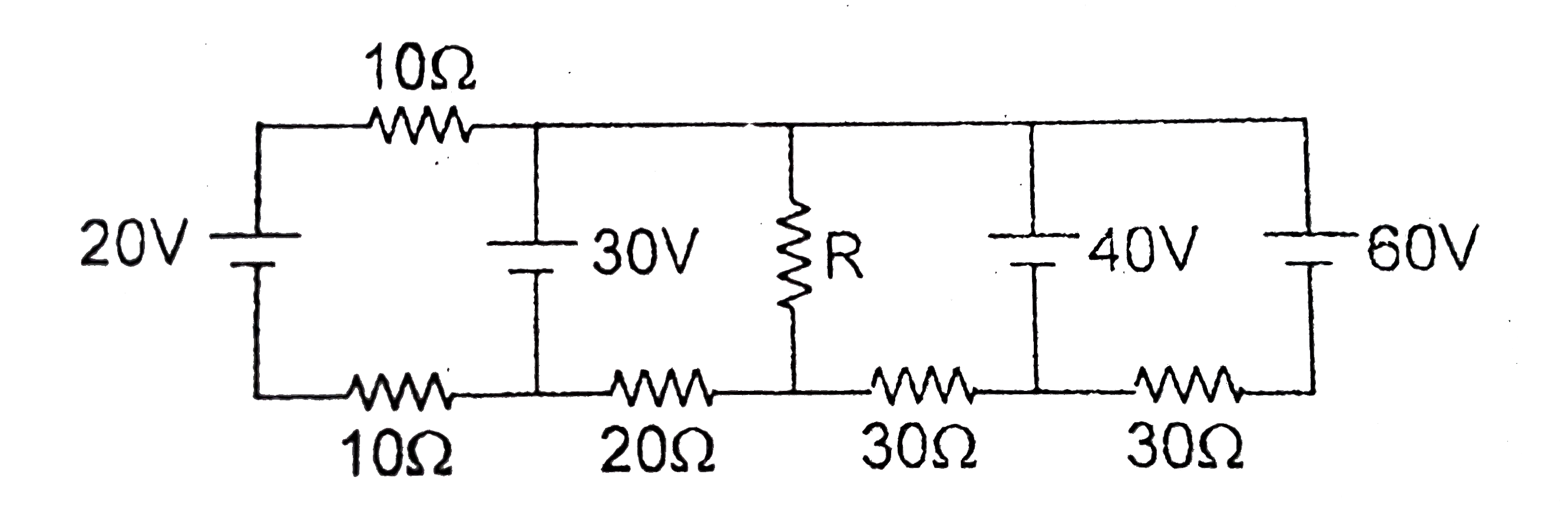
View SolutionTwo wires having resistance R and 2 R are connected in parallel, the ratio of heat generated in 2 R and R is
View Solution
