Method 3 of W
Mass of a piston shown in Fig. is m and area of cross-section is A. Initially spring is in its natural length. Find work done by the gas.

The correct Answer is:A, B
In the given condition, work is done by the gas only against spring force kx. This force is a variable force. Hence,
W=∫x0(kx)dx=12kx2
Topper's Solved these Questions
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Example Type 1
2 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Example Type 2
1 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEYCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions
10 Videos
Similar Questions
2.00 mol of a monatomic ideal gas (U=1.5nRT) is enclosed in an adiabatic, fixed , vertical cylinder fitted with a smooth, light adiabatic piston.the piston is connected to a vertical spring of spring constant 200Nm−1 as shown in .the area of cross section of the cylinder is 20.0cm2. initially, the spring is at its natural length and the temperature of the gas is at its natural length and the temperature of the gas is 300 K. the atmosphere pressure is 100 kPa. the gas is heated sloewly for some time by means of an electric heater so as to move the poston up through 10 cm. find (a) the work done by the gas (b) the final temperature of the gas and (c ) the heat supplied by the heater.

View SolutionA non conducting piston of mass m and area of cross section A is placed on a non conducting cylinder as shown in figure. Temperature, spring constant, height of the piston are given by T,K,h respectively. Initially spring is relaxed and piston is at rest. Find
(a) Number of moles
(b) Work done by gas to displaced the piston by distance d when the gas is heated slowly.
(c ) Find the final temperature

View Solution
Knowledge Check
A fixed container is fitted with a piston which is attached to a spring of spring constant k. The other and of the spring is attached to a rigid wall. Initially the spring is in its natural length and the length of container between the piston and its side wall is L. Now an dideal diatomic gas is slowly filled in the container so that the piston moves quasistatically. It pushed the piston by x so that the spring now is compressed by x. The total rotaional kinetic energy of the gas molecules in terms of the displacement x of the piston is (there is vacuum outside the container)
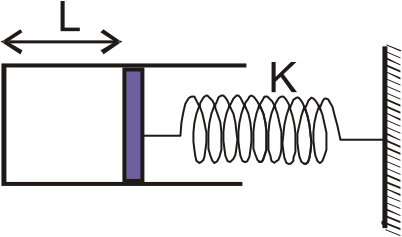 AkxLB4kxLCkx(x+L)D2kx2L
AkxLB4kxLCkx(x+L)D2kx2LFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.
 AmgBmg/2C3mg/2D2 mg
AmgBmg/2C3mg/2D2 mgTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring on each mass is
A12kx2B−12kx2C14kx2D−14kx2
Two equal masses are attached to the two end of a spring of force constant k the masses are pulled out symmetrically to stretch the spring by a length 2x0 over its natural length. Find the work done by the spring on each mass.
View SolutionA bar of mass m and length l is hanging from point A as shown in the figure . If the Young's modulus of elasticity of the bar is Y and area of cross - section of the wire is A, then the increase in its length due to its own weight will be

View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled a part symmetrically to stretch the spring by a length x over its natural length. The work done by the spring on each mass is.
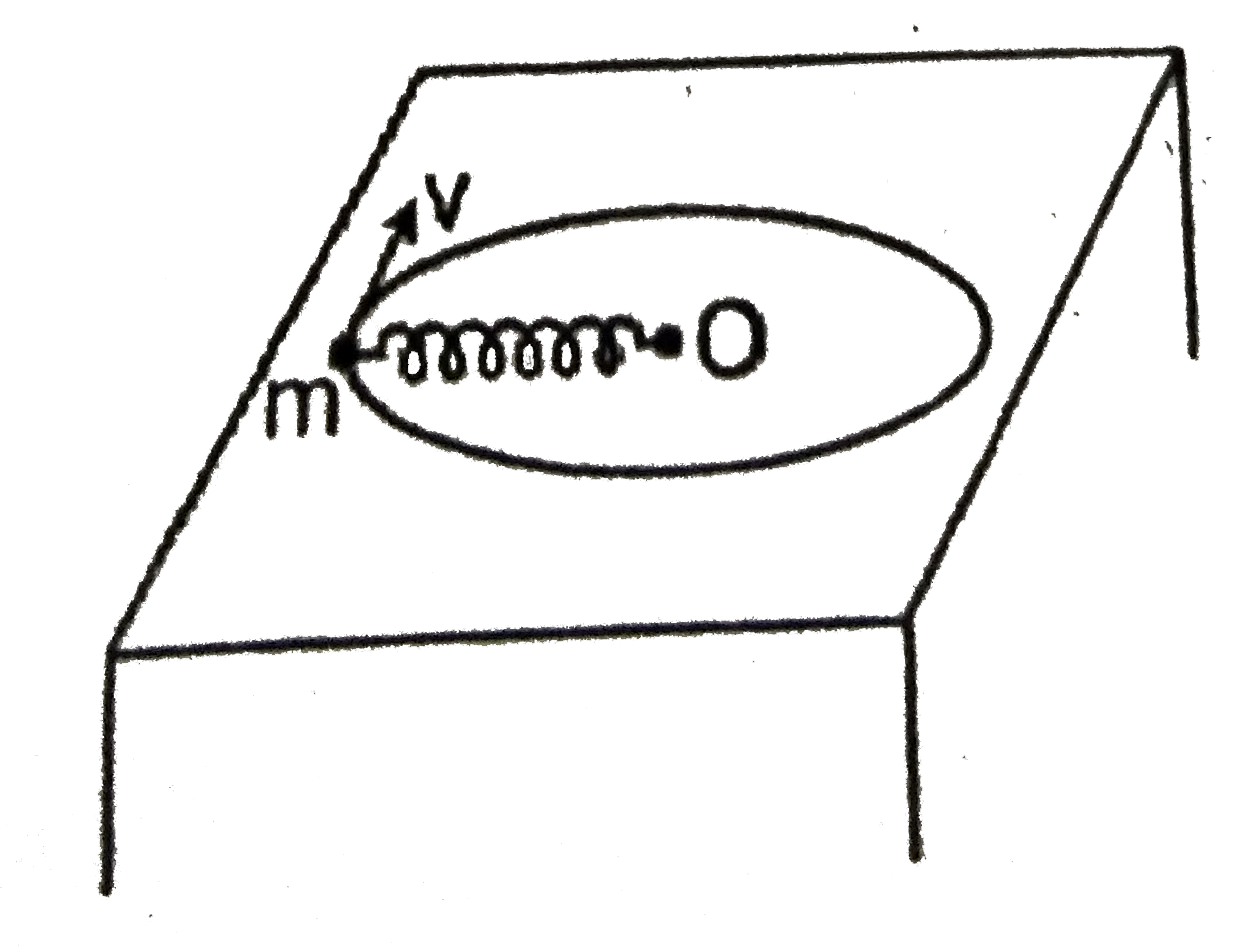
View SolutionMass m is connected with an ideal spring of natural length l whose other end is fixed on a smooth horizontal table. Initially spring is in its natural length l. Mass m is given a velocity 'v' perpendicular to the spring and released . The velocity perpendicular to the spring when its length l+x , will be
View SolutionA block of mass m is placed on a smooth block of mass M=m with the help of a spring as shown in the figure. A velocity v0 is given to upper block when spring is in natural length. Find maximum compression in the spring.
View Solution
