An ideal monoatomic gas is confined in a cylinder by a spring-loaded piston of cross-section 8.0×10−3m2. Initially the gas is at 300K and occupies a volume of 2.4×10−3m3 and the spring is in its relaxed (unstretched, unompressed) state, fig. The gas is heated by a small electric heater until the piston moves out slowly by 0.1m. Calculate the final temperature of the gas and the heat supplied (in joules) by the heater. The force constant of the spring is 8000N/m, atmospheric pressure is 1.0×105Nm−2. The cylinder and the piston are thermally insulated. The piston is massless and there is no friction between the piston and the cylinder. Neglect heat loss through lead wires of the heater. The heat capacity of the heater coil is negligible. Assume the spring to be massless.

The correct Answer is:A, B
(a) p1V1T1=p2V2T2
T2=(p2V2T1p1V1) …(i)

Here,
p1=1.0×105N/m2
V1=2.4×10−3m3
T1=300K
p2=p1+kxA
=1.0×105+8000×0.18×10−3
=2.0×105N/m2
V2=V1+Ax
=2.4×10−3+8×10−3×0.1
=3.2×10−3m3
Substituting in Eq. (i), we get
T2=800K
(b) Heat supplied by the heater,
Q=W+ΔU
Here,
ΔU=nCVΔT
=(p1V1RT1)(32R)(800−300)
=(1.0×105)(2.4×10−3)(1.5)(500)(300)
=600J
W=12kx2+p1ΔV
=12×(8000)(0.1)2+(1.0×105)(0.1)(8×10−3)
=(40+80)J=120J
∴ Q=600+120=720J
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Passage II3videos
LAWS OF THERMODYNAMICS
- BOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery39videos
LAWS OF MOTION
- BOOK - DC PANDEYCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions10videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
Similar Questions
One mole of a monoatomic ideal gas is taken through the cycle ABCDA as shown in the figure.
TA=1000K and 2pA=3pB=6pC

[Assume(23)0.4=0.85 and R=253JK−1mol−1]
The temperature at B is04:34View SolutionA rigid ball of mass m strikes a rigid wall at 60∘ and gets reflected without loss of speed as shown in the figure. The value of impulse imparted by the wll on the ball will be
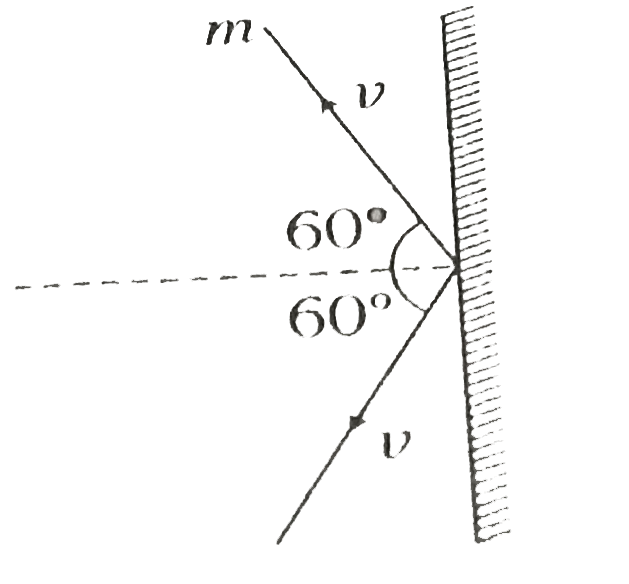 11:04View Solution
11:04View SolutionTwo parallel, long wires carry currents t1andt2 with t1>t2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 10 μT. If the direction of i2 is reversed, the field becomes 30 μT. Find the ratio i1i2.
07:26View SolutionAn ideal monatonic gas is confined in a cylinder by a spring-loaded piston of cross section 8.0×10−3m2.initially the gas is at 300K and occupies a volume of 2.4×10−3m−3 and the sprinng is in its relaxed state. The gas is heated by a small heater until the piston moves out slowly by 0.1m. Calculate the final tenoerature of the gas. The force constant if the spring is 8000Nm−1,and the atmospheric pressure is 1.0×105Nm−2.Htecyl∈derandtheπs→narethermally∈sylated.Theπs→nandthespr∈garemass≤ssandthereisnoictionbetweentheπs→nandthecyl∈der.Neg≤ctanyheat−lossthroughthe≤adwiresoftheheater.Theheat∩acityoftheheatercoilis¬ligib≤.
 09:46View Solution
09:46View SolutionAn ideal monoatomic gas is confined in a horizontal cylinder by a spring loaded piston (as shown in the figure). Initially the gas is at temperature T_1 , pressure P_1 and volume V_1 and the spring is in its relaxed state. The gas is tehn heated very slowly to temperature T_2 ,pressure P_2 and volume V_2 . During this process the piston moves out by a distance x. Ignoring the friction between the piston and the cylinder, the correct statement (s) is (are)
03:13View SolutionAn ideal monatomic gas is confined in a cylinder by a spring-loaded piston of cross-section 8.0xx10^-3m^2 . Initially the gas is at 300K and occupies a volume of 2.4xx10^-3m^3 and the spring is in its relaxed (unstretched, unompressed) state, fig. The gas is heated by a small electric heater until the piston moves out slowly by 0.1m. Calculate the final temperature of the gas and the heat supplied (in joules) by the heater. The force constant of the spring is 8000 N//m , atmospheric pressure is 1.0xx10^5 Nm^-2 . The cylinder and the piston are thermally insulated. The piston is massless and there is no friction between the piston and the cylinder. Neglect heat loss through lead wires of the heater. The heat capacity of the heater coil is negligible. Assume the spring to be massless.
View SolutionTwo moles of an ideal monoatomic gas are confined within a cylinder by a massless and frictionless spring loaded piston of cross-sectional area 4 xx 10^(-3)m^(2) . The spring is, initially in its relaxed state. Now the gas is heated by an electric heater, placed inside the cylinder, for some time. During this time, the gas expands and does 50J of work in moving the piston through a distance 0.10m . The temperature of the gas increases by 50K . Calculate the spring constant and the heat supplied by the heater. P_(atm) = 1 xx 10^(5)N//m^(2)R = 8.314 J//mol-K
11:32View Solution2 moles of a diatomic gas are enclosed in a cylinder piston arrangment. The area of cross section and mass of the piston are 1 cm^(2) and 1 kg respectively. A heater is supplying heat to the gas very slowly. Find heat supplied (in joule) by the heater is the piston moves through a distance of 10 cm. .
08:54View SolutionTwo moles of an ideal monoatomic gas are confined within a cylinder by a massless spring loaded with a frictionless piston of negligible mass and of cross-sectional area 4 xx 10^(-3) m^2 . The springis initially in its relaxed state. Now the gas is heated by a heater for some time. During this time the gas expands and does 50 J of work in moving the piston through a distance of 0.1 m. The temperature of the gas increases by 50 K. Calculate the spring constant and the heat supplied by the heater.
View Solutionएक सिलिण्डर में एक आदर्श एकपरमाणुक गैस, स्प्रिंग भारित व द्रव्यमानहीन पिस्टन द्वारा, जिसका परिच्छेद क्षेत्रफल A=8.0×10−3मी2 है, भरी है | प्रारम्भ में गैस का ताप 300 केल्विन तथा आयतन 2.4×10−3मी3 है तथा स्प्रिंग अपनी सामान्य अवस्था में है | गैस को एक छोटे विद्युत हीटर द्वारा तब तक गर्म किया जाता है जब तक कि पिस्टन धीरे - धीरे 0.1 मी बाहर की ओर बिना घर्षण के चलता है | गैस के अन्तिम ताप तथा हीटर द्वारा दी गई ऊष्मा की गणना कीजिए | स्प्रिंग का बल नियतांक k = 8000 न्यूटन मी−1 है तथा वायुमणडल दाब, 1.0×105 न्यूटन मी−2 है | सिलिण्डर तथा पिस्टन उष्मारोषित है | पिस्टन तथा स्प्रिंग द्रव्यमान है तथा पिस्टन तथा सिलिण्डर के बीच घर्षण नहीं है | हीटर की तारों द्वारा होने वाला ऊर्जा क्षय नगण्य है | हीटर की कुण्डलियों की उष्माधारिता नगण्य है |
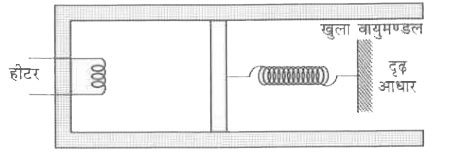 09:20View Solution
09:20View Solution2.00 mole of a monatomic ideal gas (U=1.5nRT) is enclosed in an adiabatic, fixed , vertical cylinder fitted with a smooth, light adiabatic piston. The piston is connected to a vertical spring of spring constant 200Nm−1 as shown in .the area of cross section of the cylinder is 20.0cm2. initially, the spring is at its natural length and the temperature of the gas is 300K at its natural length. the atmosphere pressure is 100 kPa. the gas is heated slowly for some time by means of an electric heater so as to move the position up through 10 cm. find (a) the work done by the gas (b) the final temperature of the gas and (c ) the heat supplied by the heater.
 06:33View Solution
06:33View SolutionTwo moles of an ideal monatomic gas are confined within a cylinder by a massless and frictionless spring loaded piston of cross-sectional area 4 xx 10^(-3) m^2 . The spring is, initially, in its relaxed state. Now the gas is heated by an electric heater, placed inside the cylinder, for some time. During this time, the gas expands and does 50 J of work in moving the piston through a distance 0.10 m. The temperature of the gas increases by 50 K. Calculate the spring constant and the heat supplied by the heater.
04:03View SolutionAn ideal monoatomic gas is confined in a cylinder by a spring-loaded piston of cross-section 8.0xx10^-3m^2 . Initially the gas is at 300K and occupies a volume of 2.4xx10^-3m^3 and the spring is in its relaxed (unstretched, unompressed) state, fig. The gas is heated by a small electric heater until the piston moves out slowly by 0.1m. Calculate the final temperature of the gas and the heat supplied (in joules) by the heater. The force constant of the spring is 8000 N//m , atmospheric pressure is 1.0xx10^5 Nm^-2 . The cylinder and the piston are thermally insulated. The piston is massless and there is no friction between the piston and the cylinder. Neglect heat loss through lead wires of the heater. The heat capacity of the heater coil is negligible. Assume the spring to be massless.
14:33View SolutionAn ideal monoatomic gas is confined in a cylinder by a spring-loaded piston of cross-section 8.0×10−3m2. Initially the gas is at 300K and occupies a volume of 2.4×10−3m3 and the spring is in its relaxed (unstretched, unompressed) state, fig. The gas is heated by a small electric heater until the piston moves out slowly by 0.1m. Calculate the final temperature of the gas and the heat supplied (in joules) by the heater. The force constant of the spring is 8000N/m, atmospheric pressure is 1.0×105Nm−2. The cylinder and the piston are thermally insulated. The piston is massless and there is no friction between the piston and the cylinder. Neglect heat loss through lead wires of the heater. The heat capacity of the heater coil is negligible. Assume the spring to be massless.
 06:28View Solution
06:28View Solution2 moles of a diatomic gas are enclosed in a cylinder piston arrangment. The area of cross section and mass of the piston are 1 cm^(2) and 1 kg respectively. A heater is supplying heat to the gas very slowly. Find heat supplied (in joule) by the heater is the piston moves through a distance of 10 cm. .
04:16View SolutionAn ideal monoatomic gas is confined in a horizontal cylinder by a spring loaded piston (as shown in the figure). Initially the gas is at temperature T1, pressure P1 and volume V1and the spring is in its relaxed state. The gas is then heated very slowly to temperature T2,pressure P2and volume V2. During this process the piston moves out by a distance x. Ignoring the friction between the piston and the cylinder, the correct statement (s) is (are)
 04:26View Solution
04:26View Solution

