Most materials have the refractive index, n>1. So, when a light ray from air enters a naturally occuring material, then by Snell's law, sinθ1sinθ2=n1n2, it is understood that the refracted ray bends towards the normal. But it never emerges on the same side of the normal as the incident ray. According to electromagnetism, the refractive index of the medium is given by the relation, n=(c/v)=±√εr,μr, where c is the speed of the electromagnetic waves in vacuum, v its speed in the medium, εr and μr are negative, one must choose the negative root of n. Such negative refractive index materials can now be artifically prepared and are called meta-materials. They exhibit significantly different optical behaviour, without violating any physical laws. Since n is negative, it results in a change in the direction of propagation of the refracted light. However, similar to normal materials, the frequency of light remains unchanged upon refraction even in meta-materials.
Answer the following questions :
Choose the correct statement.
The speed of ligth in the meta-material is v=c|n|
The speed of ligth in the meta-material is v=c|n|
The speed of ligth in the meta-material is v=c
The wavelength of the light in the meta-material (λm) is given by λm=λair|n|, Where lambda_(air) is the wavelength of the ligth in air
The correct Answer is:b
To solve the question regarding the behavior of light in metamaterials and the correct statements about the speed of light and wavelength, we can break down the solution into the following steps:
Step 1: Understand the Refractive Index
The refractive index n of a material is defined as the ratio of the speed of light in vacuum c to the speed of light in the material v:
n=cv
For most materials, n>1, meaning that light slows down when entering the material. However, in metamaterials, the refractive index can be negative.
Step 2: Analyze the Speed of Light in Metamaterials
For metamaterials with a negative refractive index, we can express the speed of light in the material as:
v=cn
Since n is negative, we can take the absolute value to ensure speed remains positive:
v=c|n|
This indicates that the speed of light in a metamaterial is inversely proportional to the absolute value of the refractive index.
Step 3: Evaluate the Given Statements
1. Speed of light in metamaterial is v=c×|n|: This is incorrect because it suggests that speed increases with increasing refractive index, which contradicts the definition.
2. Speed of light in metamaterial is v=c|n|: This is correct as derived above.
3. Speed of light in metamaterial is v=c: This is incorrect since the speed of light changes in a medium.
4. Wavelength in metamaterial is λ=λ0×n: This is incorrect because the wavelength in a medium is given by:
λ=λ0|n|
where λ0 is the wavelength in vacuum.
Step 4: Conclusion
From the analysis, the correct statement is:
- Speed of light in metamaterial is v=c|n|.
The refractive index n of a material is defined as the ratio of the speed of light in vacuum c to the speed of light in the material v:
n=cv
For most materials, n>1, meaning that light slows down when entering the material. However, in metamaterials, the refractive index can be negative.
For metamaterials with a negative refractive index, we can express the speed of light in the material as:
v=cn
Since n is negative, we can take the absolute value to ensure speed remains positive:
v=c|n|
This indicates that the speed of light in a metamaterial is inversely proportional to the absolute value of the refractive index.
1. Speed of light in metamaterial is v=c×|n|: This is incorrect because it suggests that speed increases with increasing refractive index, which contradicts the definition.
2. Speed of light in metamaterial is v=c|n|: This is correct as derived above.
3. Speed of light in metamaterial is v=c: This is incorrect since the speed of light changes in a medium.
4. Wavelength in metamaterial is λ=λ0×n: This is incorrect because the wavelength in a medium is given by:
λ=λ0|n|
where λ0 is the wavelength in vacuum.
From the analysis, the correct statement is:
- Speed of light in metamaterial is v=c|n|.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Matching Column Type2videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type14videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - MCQ2videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
Similar Questions
Most materials have the refractive index, n>1. So, when a light ray from air enters a naturally occuring material, then by Snell's law, sinθ1sinθ2=n1n2, it is understood that the refracted ray bends towards the normal. But it never emerges on the same side of the normal as the incident ray. According to electromagnetism, the refractive index of the medium is given by the relation, n=(c/v)=±√εr,μr, where c is the speed of the electromagnetic waves in vacuum, v its speed in the medium, εr and μr are negative, one must choose the negative root of n. Such negative refractive index materials can now be artifically prepared and are called meta-materials. They exhibit significantly different optical behaviour, without violating any physical laws. Since n is negative, it results in a change in the direction of propagation of the refracted light. However, similar to normal materials, the frequency of light remains unchanged upon refraction even in meta-materials.
Answer the following questions :
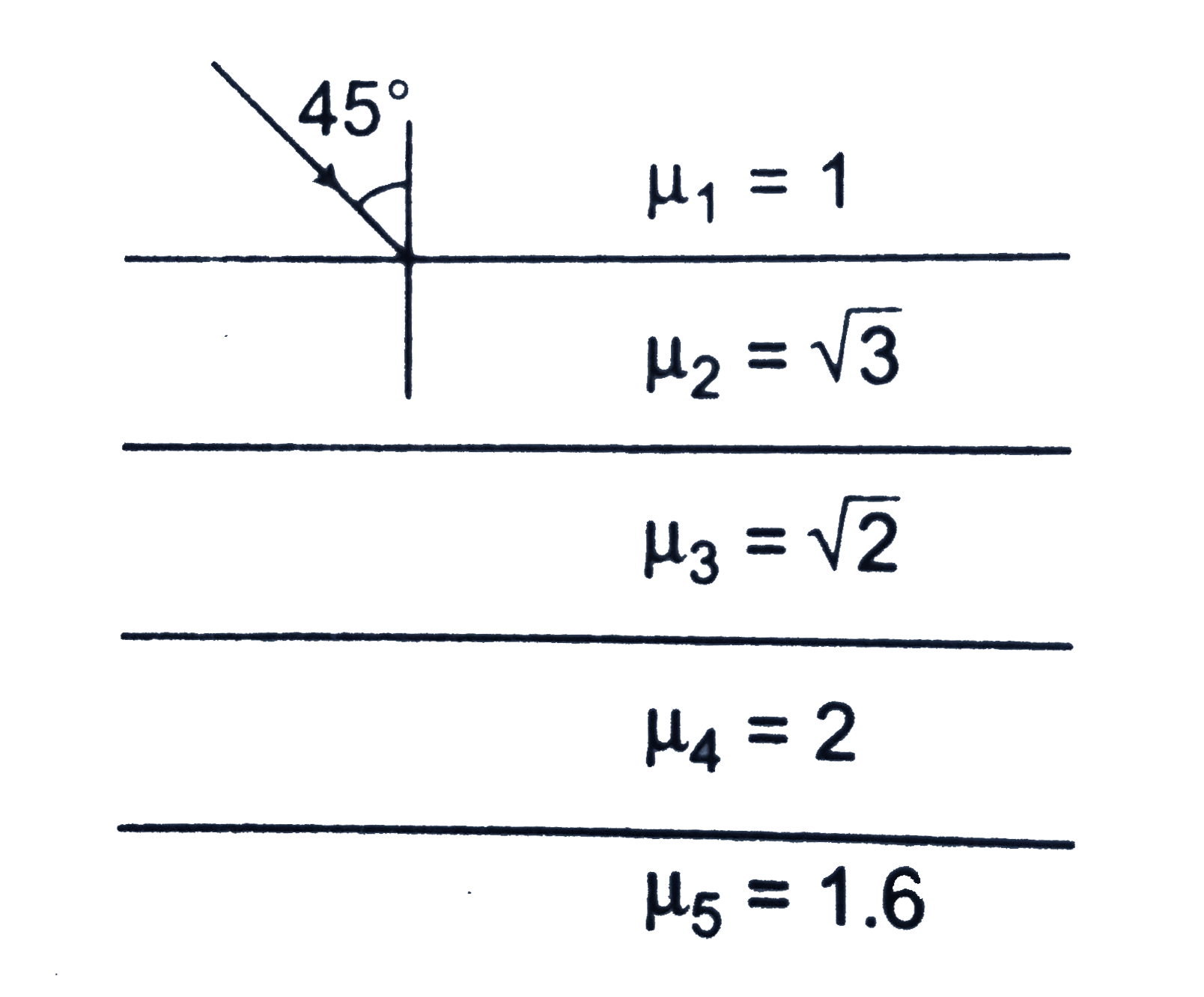
For light incident from air on a meta-material, the appropriate ray diagram isView SolutionIn the figure shown, the angle made by the light ray with the normal in the medium of refractive index √2 is
 View Solution
View SolutionWhen light rays enter the eye, most of the refraction occurs at the
View SolutionOne of the refracting surfaces of a prism of angle of 30∘ is silvered. A ray of light incident at an angle of 60∘ retraces its path. The refractive index of the material of prism is
View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5)
View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5
View SolutionWhen light travels from glass to air, the incident angle is θ1 and the refracted angle is θ2. The true relation is
View SolutionA light ray is normally incident onone face of equilateral glass prism of refractive index √2. The deviation of light ray is
View SolutionA ray of light incidents on a refracting surface at 30∘ with the surface . If the angle of refraction is 45∘ refractive index of the medium is
View SolutionThe incident ray, the _______ ray and the normal lie in the same plane during refraction.
View Solution

