Obtain an expression for the position vector of centre of mass of a two particle system.
To derive the expression for the position vector of the center of mass of a two-particle system, we can follow these steps:
1. Define the System:
Consider a two-particle system with masses m1 and m2. Let the position vectors of these masses be r1 and r2 respectively.
2. Concept of Center of Mass:
The center of mass (COM) of a system is defined as the point where the total mass of the system can be considered to be concentrated. The position vector of the center of mass rcom can be expressed in terms of the position vectors of the individual masses.
3. Total Mass:
The total mass M of the system is given by:
M=m1+m2
4. Weighted Average of Position Vectors:
The position vector of the center of mass is a weighted average of the position vectors of the individual masses. Therefore, we can express rcom as:
rcom=m1r1+m2r2M
5. Substituting Total Mass:
Substituting M=m1+m2 into the equation gives:
rcom=m1r1+m2r2m1+m2
6. Final Expression:
Thus, the final expression for the position vector of the center of mass of a two-particle system is:
rcom=m1r1+m2r2m1+m2
Consider a two-particle system with masses m1 and m2. Let the position vectors of these masses be r1 and r2 respectively.
The center of mass (COM) of a system is defined as the point where the total mass of the system can be considered to be concentrated. The position vector of the center of mass rcom can be expressed in terms of the position vectors of the individual masses.
The total mass M of the system is given by:
M=m1+m2
The position vector of the center of mass is a weighted average of the position vectors of the individual masses. Therefore, we can express rcom as:
rcom=m1r1+m2r2M
Substituting M=m1+m2 into the equation gives:
rcom=m1r1+m2r2m1+m2
Thus, the final expression for the position vector of the center of mass of a two-particle system is:
rcom=m1r1+m2r2m1+m2
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE E
1 Video
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ADVANCED PROBLEMS FOR COMPETITIONS
20 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SHORT ANSWER QUESTIONS II.
2 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
Knowledge Check
The centre of mass of two particles system lies
Aat the midpoint on the line joining the two particles.Bat one end of line joining the two particlesCon the line perpendicular to the line joining two particlesDon the line joining the two particlesThe position of centre of mass of a system of particles does not depend upon
Amasses of particlesBforces on particlesCposition of the particlesDrelative distance between the particlesThree particles , each of mass m, are placed at the vertices of a right angled triangle as shown in figure. The position vector of the center of mass of the system is (O is the origin and ˆi,ˆj,ˆk are unit vectors)
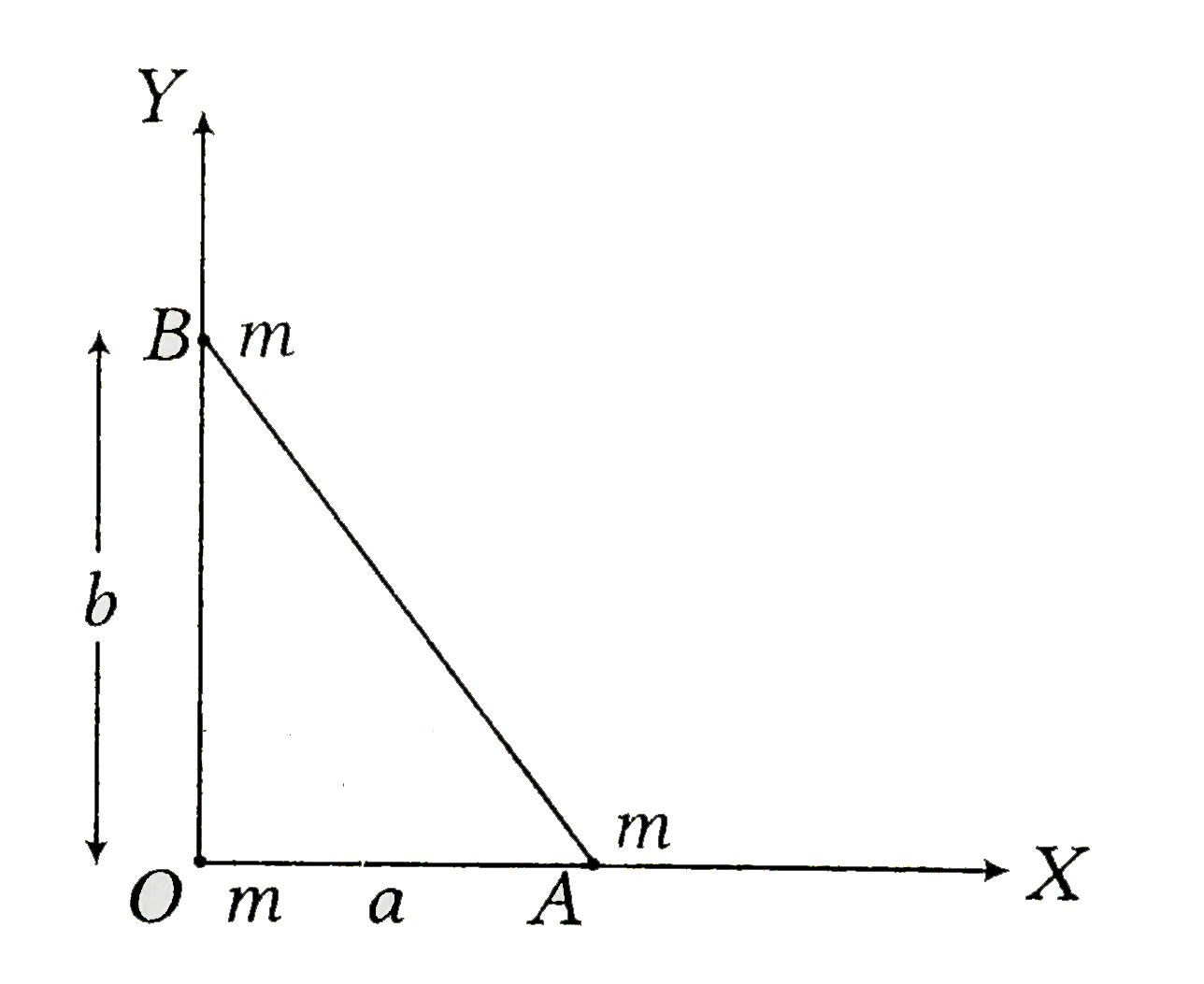 A13(aˆi−bˆj)B23(aˆi−bˆj)C23(aˆi+bˆj)D13(aˆi+bˆj)
A13(aˆi−bˆj)B23(aˆi−bˆj)C23(aˆi+bˆj)D13(aˆi+bˆj)
Find out the position of centre of mass of two particle system.
View SolutionWhat is the position vector of centre of mass of two particles of equal masses ?
View SolutionWrite an expression for the velocity of the centre of mass of a system of particles.
View SolutionWrite an expression for the centre of mass of& two partide system
View SolutionThe position of center of mass of a system of particles does not depend upon the
View Solution