Obtain the answers to (a) and (b) in Q .15, if the circuit is connected to 110 V, 12 kHz supply. Hence explain the statement that a capacitor is a conductor at very high frequencies. Compare this behaviour with that of a capacitor in d.c. after the steady state.
Capacitance of the capacitor, C=100μF=100×10−6F
Resistance of the resistor, R=40Ω
Supply voltage, V=110V
Frequency of the supply. V=12KHz=12×103Hz
=ω=2nv=2×n×12×10303
=24nxx 103 rad/s
Peak voltage, V∘=V√2=110√2V
I∘=V∘√R2+1ω2C2
Maximum current.
=110√2√(40)2+(24π×103×100×10−6)2
For an d RC circuit the voltage lags behind the current by a phase angle of ϕ given as:
tanϕ=1ωCR=1ωCR
=0.2π180rad
∴ Time lag =ϕω
=0.2π180×24π×103=1.55xx10−3s=0.04μs
Hence ϕ tends to become zero at high frequencies. At a high frequency capacitor C acts as a conductor.
In a dc circuit, after the steady state is acheived ω=0 . Hence, capacitor C amounts to an open circuit.
Topper's Solved these Questions
Similar Questions
Obtain the answers to (a) and (b) above in Exercise 7.15 if the circuit is connected to a 110 V, 12 kHz supply ? Hence, explain the statement that a capacitor is a conductor at very high frequencies. Compare this behaviour with that of a capacitor in a d.c. circuit after the steady state
View SolutionObtain the answers to (a) and (b) Q.13, if the circuit is connected to a high frequency supply (240 V , 10 kHz). Hence explain statement that at very high frequency. Inductor in circuit nearly amount to open circuit. How does an indcutor behave in a d.c. circuit after the steady state ?
View Solution
Knowledge Check
A capacitor with capacitance C is charged to Q0 and then connected in the circuit shown. When key is closed, what is charge on this capacitor in steady state?
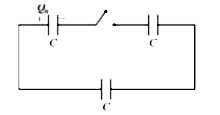 AQ03B2Q03CQ02D3Q02
AQ03B2Q03CQ02D3Q02
Obtain the answers (a) to (b) in Exercise 7.13 if the circuit is connected to a high frequency supply (240 V, 10 kHz). Hence, explain the statement that at very high frequency, an inductor in a circuit nearly amounts to an open circuit. How does an inductor behave in a d.c. circuit after the steady state ?
View SolutionA 60 μF capacitor is connected to a 110 V, 60 Hz a.c. supply. Determine the rms value of the current in the circuit.
View SolutionA 60μF capacitor is connected to a 110 V, 60 Hz a.c. supply Determine the r.m.s value of current in the circuit.
View SolutionA capacitor having a capacitance of 200 μF is charged to a potential difference of 20V. The charging battery is disconnected and the capacitor is connected to another battery of emf 10V with the positive plate of the capacitor joined with the positive terminal of the battery.
(a) Find the charges on the capacitor before and after the reconnection in steady state.
(b) Find the net charge flown through the 10 V battery
Is work done by the battery or is it done on the battery? Find its magnitude.
(d) Find the decrease in electrostatic field energy.
(e) Find the heat developed during the flow of charge after reconnection .
View SolutionAs we know in steady state charge on a capacitor is given as Q=CV which also implies C=Q/V. So can we say in steady state capacitance is proportional to the supplied charge Q.
View SolutionA 10μF capacitor in series with a 40Ω resistance is connected to a 110 V, 60Hz supply. (a) What is the maximum current in the circuit ? (b) What is the time lag between current maximum and voltage maximum ?
View SolutionA 100 uF capacitor in series with a 40 Ω resistance is connected to a 110 V, 60 Hz supply.
(a) What is the maximum current in the circuit ?
(b) What is the time lag between the current maximum and the voltage maximum ?
View Solution
