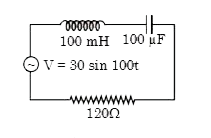
Obtain the resonance angular frequency for the circuit shown in figure.

Here inductor L and resistance R are in series. If Z1 is its resultant impedance then
Z1=R+jXL=R+jωL
This Z1 and capacitor C are in parallel . So the resultant impedance Z for about circuit.
1Z=1R+jωL+jωC ⎡⎣∴1−1ωCj=−ωCj=jωC⎤⎦
=R−jωLR2+ω2L2+jωC
[ Multiplying and dividing the first term on the right hand side by R=jωL]
=R+j(ωCR2+ω2L2C−ωL)R2+ω2L2
∴Z=R2+ω2L2R+j(ωCR2+ω2L2C−ω)
The imaginary part (coefficient of j ) in the denominator of the above equation should be zero, for Z to be maximum.
∴ωCR2+ω3L2C−ωL=0
∴ω2L2C=L−CR2
∴ω2=1LC−R2L2
∴ω=√1LC−R2L2
Topper's Solved these Questions
- ALTERNATING CURRENTS BOOK - KUMAR PRAKASHANCHAPTER - ALTERNATING CURRENTS EXERCISE - SECTION-C NCERT EXEMPLAR (MCQs)
7 Videos
- ALTERNATING CURRENTS BOOK - KUMAR PRAKASHANCHAPTER - ALTERNATING CURRENTS EXERCISE - SECTION-C NCERT EXEMPLAR (More than one Options)
6 Videos
- ALTERNATING CURRENTS BOOK - KUMAR PRAKASHANCHAPTER - ALTERNATING CURRENTS EXERCISE - SECTION B NUMERICALS (ADDITONAL EXERCISE )
32 Videos
- ATOMSBOOK - KUMAR PRAKASHANCHAPTER - ATOMSEXERCISE - Section-D -MCQs asked in GUJCET / Board Exam
34 Videos
Similar Questions
Knowledge Check
The natural frequency of the circuit shown in the figure is
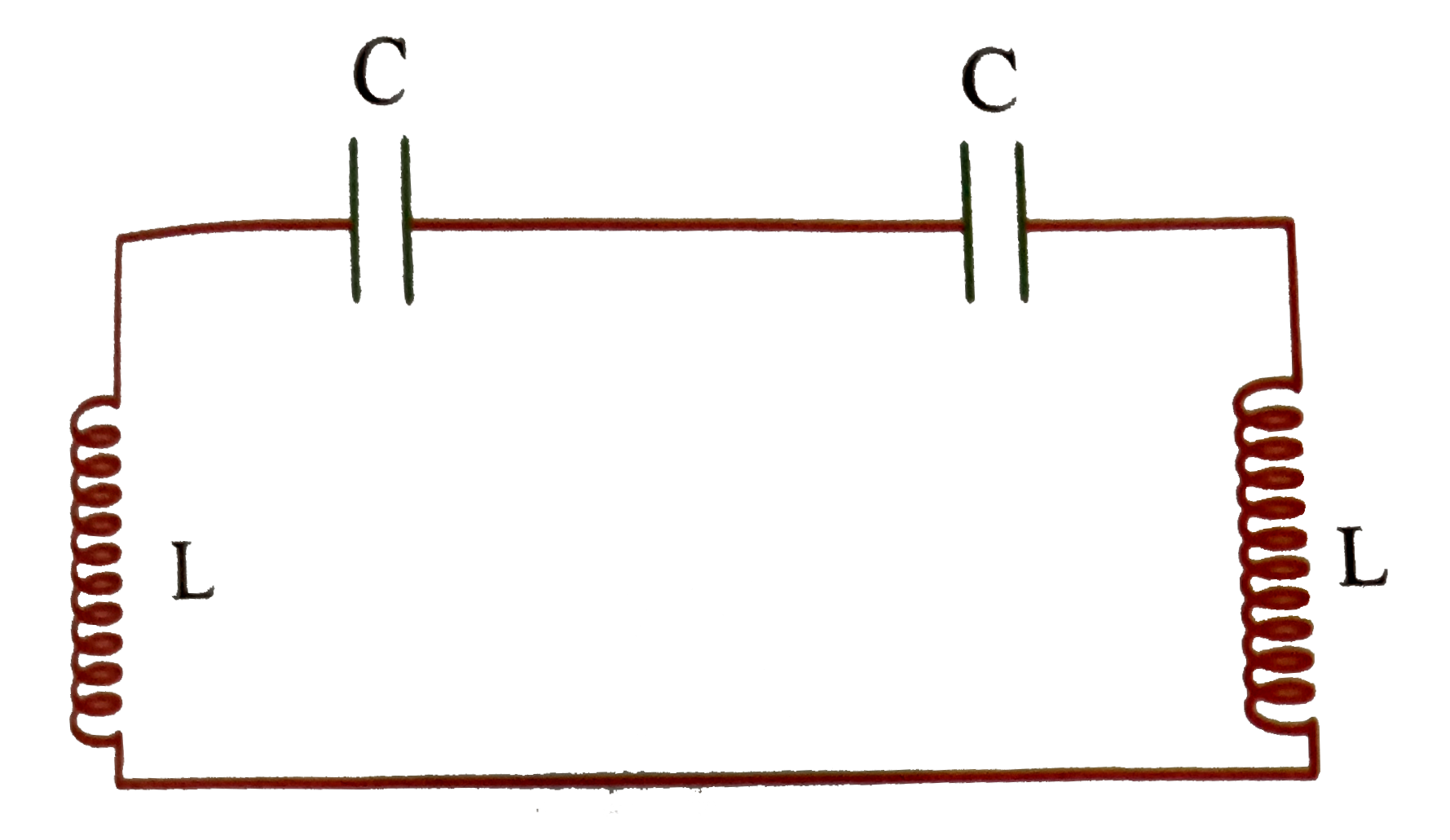 A12π√LCB1π√LCC2π√LCDnone
A12π√LCB1π√LCC2π√LCDnoneThe resonant frequency of an L - C circuit is
A12π√LCB12π√LCC12π√LCD12π√CLAn inductor L and a capacitor C are connected in the circuit as shown in the figure. The frequency of the power supply is equal to the resonant frequency of the circuit. Which ammeter will read zero ampere
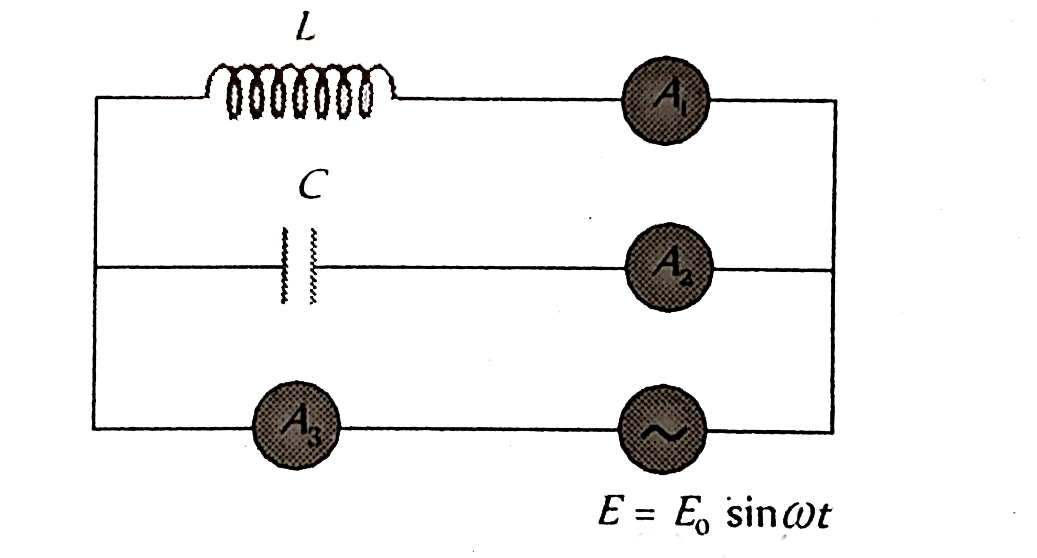 AA1BA2CA3DNone of these
AA1BA2CA3DNone of these
Phase relationship between current (l) and applied voltage (E) for a series LCR circuit is shown here. ω0 = Resonant angular frequency of the circuit and ω= Applied angular frequency .
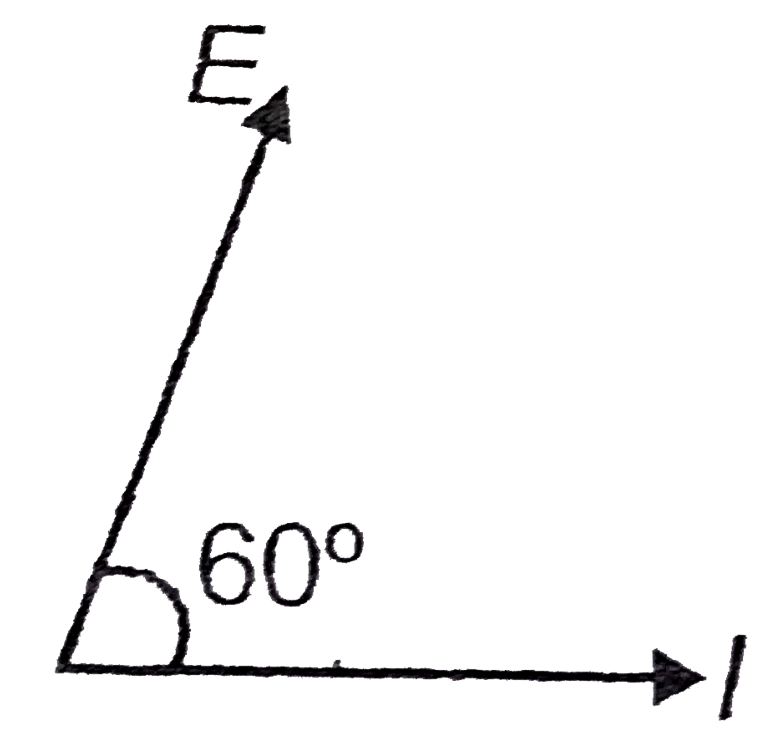
View SolutionPhase relationship between current (l) and applied voltage (E) for a series LCR circuit is shown here. ω0 = Resonant angular frequency of the circuit and ω= Applied angular frequency .

View SolutionAn inductor L and a capacitor C are connected in the circuit as shown in the figure. The frequency of the power supply is equal to the resonant frequency of the circuit. Which ammeter will read zero ampere

View SolutionAn inductor of 10mH an a capacitor of 16mF are connected in the circuit as shown in figure The frequency of the power supply is equal to the resonant frequency of the circuit Which ammeter will read will zero ampere
 .
.
View SolutionIn a series L-C-R circuit shown in the figure , what is the resonance frequency and the current at the resonating frequency?
View Solution