On a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−axis ( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x− axis , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x− axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle θ made by the velocity vector of the ball with the x−axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(3).

If both Assetion and Reason are correct but Reason is the correct explanation of Assertion.
If both Assetion and Reason are correct but Reason is not the correct explanation of Assertion.
If Asserion is true but Reason is false
If Asserion is false but Reason is true
The correct Answer is:D
(d) Component of A along B=A.B|B|=ABcosθB=Acosθ component of B along A=A.B|A|=ABcosθA=Bcosθ
Topper's Solved these Questions
Similar Questions
Knowledge Check
A line makes an angle π4 with each y-axis and z-axis. The angle that it makes with the x - axis is
Aπ2Bπ4CπDπ6
A line makes an angle of 600 with each of X-axis and Y-axis. Find the acute angle made by the line with Z-axis.
View SolutionA line makes an angle of 600 with each of X-axis and Y-axis. Find the acute angle made by the line with Z-axis.
View SolutionA vector lying in x-y plane has a magnitude 3, and makes an angle 30∘ with the x-axis. Find its components along the two axes.
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
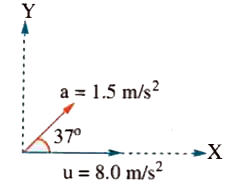
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.
View SolutionA mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin.
View SolutionFind the equation of the straight line which cuts off an intercept-5 from the y-axis and makes an angle of sin−1(1213) with the x-axis.
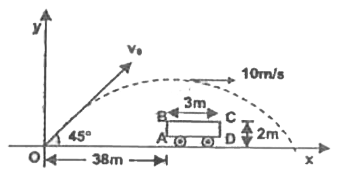
View SolutionA ball is thrown from the origin in the x-y plane with velocity 28.28m/s at an angle of 45∘ with x-axis.At the same instant a trolley also starts moving with uniform velocity of 10m/s along the positive x-axis . Initially , the trolley is located at 38m from the origin. Determine the time at which the ball hits the trolley.
View Solution

