A vector of magnitude 13 makes an angle 65.37∘ with the x-axis . What is its component along positive y-axis ?
The correct Answer is:11.82
To find the component of a vector along the positive y-axis, we can use the following steps:
Step 1: Identify the given values
- Magnitude of the vector (R) = 13
- Angle with the x-axis (θ) = 65.37°
Step 2: Use the formula for the vertical component
The vertical component (Vy) of the vector can be calculated using the formula:
Vy=R⋅sin(θ)
Step 3: Substitute the values into the formula
Now, substituting the values we have:
Vy=13⋅sin(65.37°)
Step 4: Calculate the sine of the angle
Using a calculator or trigonometric tables, we find:
sin(65.37°)≈0.91
Step 5: Calculate the vertical component
Now, substituting the sine value back into the equation:
Vy=13⋅0.91
Vy≈11.83
Final Answer
The component of the vector along the positive y-axis is approximately 11.83.
---
- Magnitude of the vector (R) = 13
- Angle with the x-axis (θ) = 65.37°
The vertical component (Vy) of the vector can be calculated using the formula:
Vy=R⋅sin(θ)
Now, substituting the values we have:
Vy=13⋅sin(65.37°)
Using a calculator or trigonometric tables, we find:
sin(65.37°)≈0.91
Now, substituting the sine value back into the equation:
Vy=13⋅0.91
Vy≈11.83
The component of the vector along the positive y-axis is approximately 11.83.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -A Objective (one option is correct)
50 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -B Objective (one option is correct)
29 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - llustration 1 :
1 Videos
- MOCK_TEST_17BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOCK_TEST_17EXERCISE - Example
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
A vector lying in x-y plane has a magnitude 3, and makes an angle 30∘ with the x-axis. Find its components along the two axes.
View SolutionA displacement vector of magnitude 4 makes an angle 30∘ with the x-axis. Its rectangular components in x-y plane are
View SolutionA displacment vector fo magnitude 4 makes an angle 30∘ with the x-axis. Its rectangular components in x-y plane are
View SolutionX- component of →a is twice of its Y- component. If the magnitude of the vector is 5√2 and it makes an angle of 135∘ with z-axis then the components of vector is:
View SolutionWrite a vector of magnitude 12 units which makes 450 angle with X-axis 600 angle with Y-axis and an obtuse angle with Z-axis.
View SolutionVector →A of magnitude 4 units is directed along the positive x-axis. Another vector →B of magnitude 3 units lies in the x-y plane and is directed along 30∘ with the positive x-axis is as shown in figure. The magnitude of dot product →A.→B is:
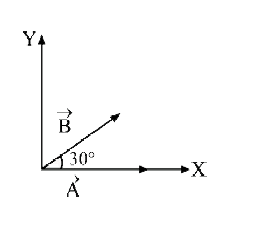
View SolutionA vector having magnitude 30 unit makes equal angles with each of X,Y, and Z -axes The components of vector along each of X,Y,and Z -axes are
View SolutionFind the equation of the line which makes an angle of 750 with x-axis and cuts an intercept of length 3 on the positive direction of y-axis.
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
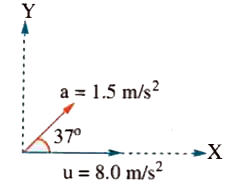
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.
View SolutionFind a vector →a of magnitude 5√2 making an angle of π4 with x-axis, π2 with y-axis and an acute angle θ with z-axis.
View Solution
