Question

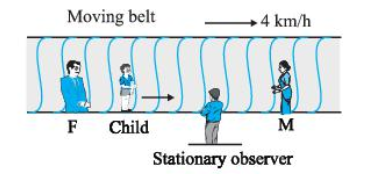
On a long horizontally moving belt, a child runs to an fro with a speed $9km{h}^{-1}$ ( with respect to the belt) between his father and mother located 50m a part on the moving belt. The belt moves with a speed of 4 $km{h}^{-1}$. For an observer on a stationery platform outside, what is the
(i) speed of the child running in the direction of motion of the belt,
(ii) speed of the child running opposited to the direction of motion of the belt , and (iii) time taken by child in (i) and (ii) ?
which of the answers alter if motion is viewed by one of the parents?

Options

A. `4 km h^(-1), 5 km h^(-1)`
B. `5 km h^(-1) ,9 km h^(-1)`
C. `9 km h^(-1), 4 km h^(-1)`
D. `13 km h^(-1), 5 km h^(-1)`

Answer

D

Explanation

To solve the problem step by step, we will analyze the motion of the child running on a moving belt, considering the speeds involved and the distances covered.

Step 1: Understand the Given Information
- Speed of the child with respect to the belt: \( v_{cb} = 9 \, \text{km/h} \)
- Speed of the belt: \( v_b = 4 \, \text{km/h} \)
- Distance between the father and mother: \( d = 50 \, \text{m} \)

Step 2: Convert Units
Since we need to calculate time in seconds, we should convert the speeds from km/h to m/s.
- To convert km/h to m/s, we use the conversion factor \( \frac{5}{18} \).

\( v_{cb} = 9 \, \text{km/h} \times \frac{5}{18} = 2.5 \, \text{m/s} \)
\( v_b = 4 \, \text{km/h} \times \frac{5}{18} = \frac{20}{18} \approx 1.11 \, \text{m/s} \)

Step 3: Calculate the Speed of the Child in the Direction of the Belt
When the child runs in the same direction as the belt, the speeds add up:
\( v_{c\text{(forward)}} = v_{cb} + v_b = 9 \, \text{km/h} + 4 \, \text{km/h} = 13 \, \text{km/h} \)

Step 4: Calculate the Speed of the Child Opposite to the Direction of the Belt
When the child runs in the opposite direction to the belt, the speeds subtract:
\( v_{c\text{(backward)}} = v_{cb} - v_b = 9 \, \text{km/h} - 4 \, \text{km/h} = 5 \, \text{km/h} \)

Step 5: Calculate Time Taken in Both Directions
The time taken to cover the distance of 50 m can be calculated using the formula:
\( \text{Time} = \frac{\text{Distance}}{\text{Speed}} \)

1. Time taken when running in the direction of the belt:
\( t_{forward} = \frac{50 \, \text{m}}{v_{c\text{(forward)}}} = \frac{50}{2.5} = 20 \, \text{s} \)

2. Time taken when running opposite to the direction of the belt:
\( t_{backward} = \frac{50 \, \text{m}}{v_{c\text{(backward)}}} = \frac{50}{1.39} \approx 36 \, \text{s} \)

Step 6: Summary of Results
- Speed of the child running in the direction of the belt: \( 13 \, \text{km/h} \)
- Speed of the child running opposite to the direction of the belt: \( 5 \, \text{km/h} \)
- Time taken in the direction of the belt: \( 20 \, \text{s} \)
- Time taken opposite to the direction of the belt: \( 36 \, \text{s} \)

Step 7: Effect of Observing from One of the Parents
If one of the parents observes the child, they are stationary relative to the belt. Therefore:
- The speed of the child will be \( 9 \, \text{km/h} \) for both directions, as they are not considering the motion of the belt.
- The time taken will remain the same as calculated above since the distance remains constant.