On connecting a battery to the two corners of a diagonal of a square conductor frame of side a the magnitude of the magnetic field at the centre will be
μ0πa
μ0√2πa
Zero
√2μ0πa
The correct Answer is:C
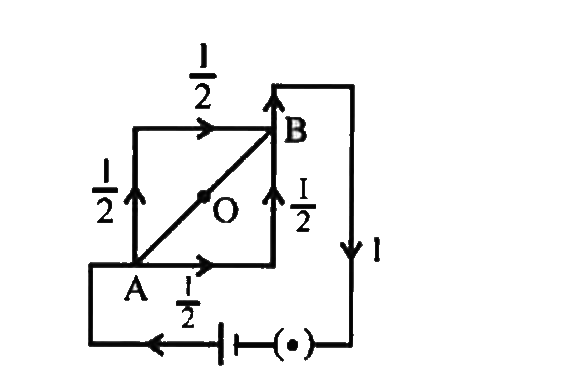
The current will be divided as I2andI2 at A and we get two sets of parallel wires carrying currents in the same direction. But the magnetic fields produced by them at the centre O will be equal and opposite. Hence the resultant magntic field at teh centre will be zero.
Topper's Solved these Questions
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - MCQ (HIGHER LEVEL)
34 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - MCQ (GRAPHICAL MCQS)
2 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - MCQ (HIGHER LEVEL)
3 Videos
- FRICTIONAL IN SOLIDS AND LIQUIDS BOOK - MARVEL PUBLICATIONCHAPTER - FRICTIONAL IN SOLIDS AND LIQUIDS EXERCISE - TEST YOUR GRASP
10 Videos
- MAGNETISMBOOK - MARVEL PUBLICATIONCHAPTER - MAGNETISMEXERCISE - TEST YOUR GRASP
10 Videos
Similar Questions
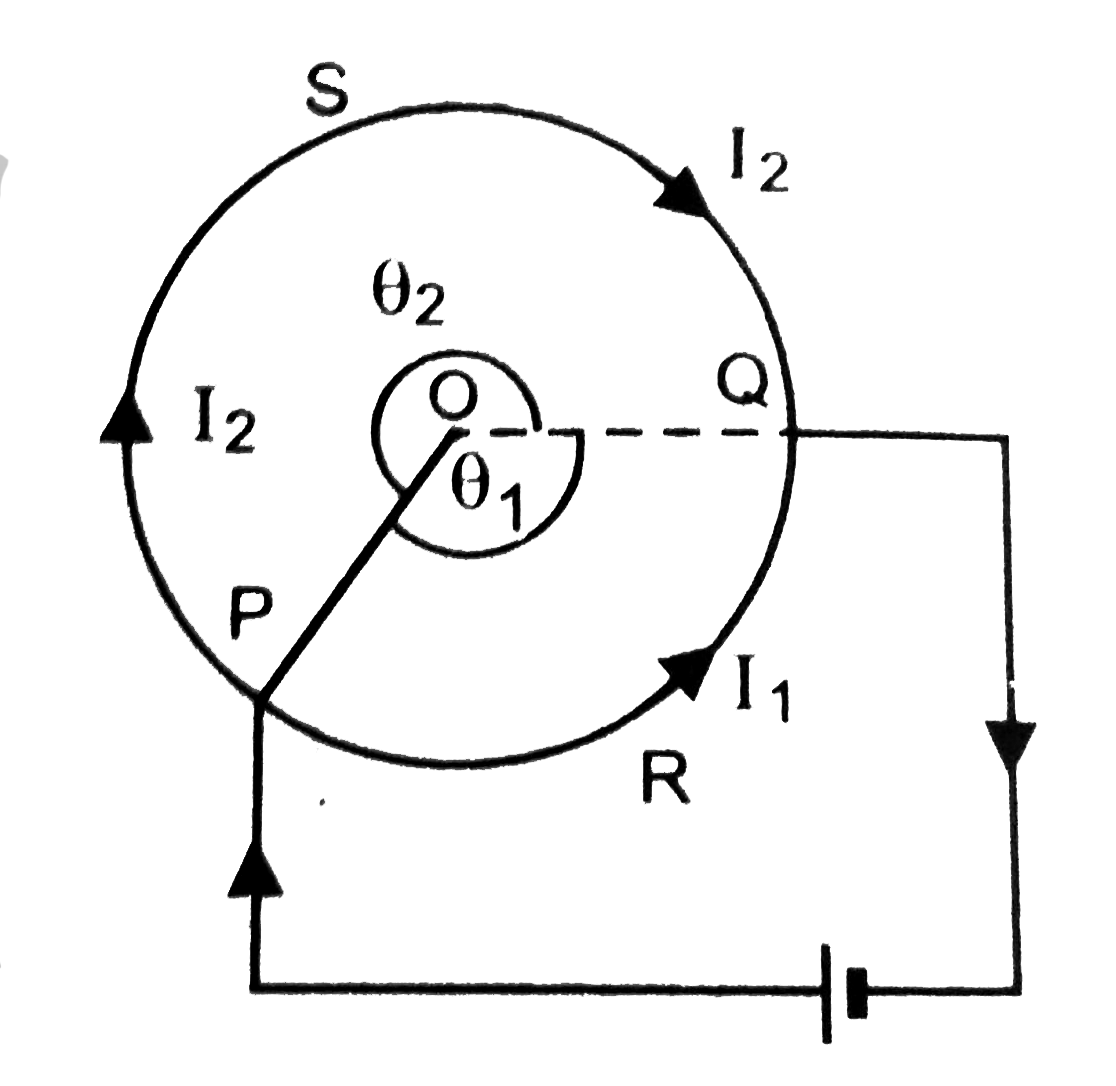
A cell is connected across two points P and Q of a uniform circular conductor, figure. Prove that the magnetic field at its centre O will be zero.
View SolutionA square loop of side length L carries a current which produces a magnetic field B0 at the centre (O) of the loop. Now the square loop is folded into two parts with one half being perpendicular to the other (see fig). Calculate the magnitude of magnetic field at the centre O.

View Solution
Knowledge Check
A square loop of side a carries a current I. The magnetic field at the center of the loop is
A2μ0I√2πaBμ0I√2πaC4μ0I√2πaDμ0IπaA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
Aindependent of LBproportional LCinversely proportional to LDlinearly proportional to LThe magnetic field at the centre of square of side a is
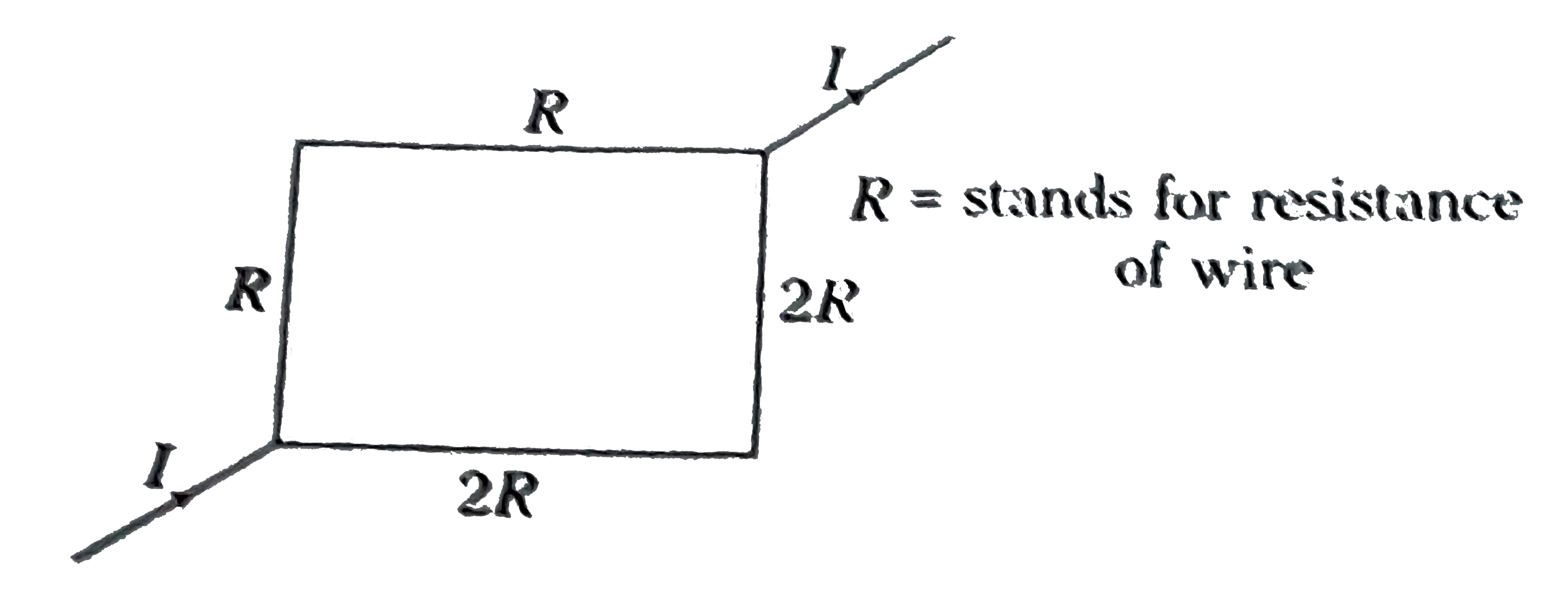 A√2μ0πaB√2μ0I3πaC23μ0IaDzero
A√2μ0πaB√2μ0I3πaC23μ0IaDzero
Two long straight conductors are connected radially to two arbitary points A and B of a circular conductor. Calculate the magnetic field at the center of the coil.
View SolutionA current of 2A enters at the corner d of a square frame abcd of side 10cm and leaves at the opposite corner b.A magnetic field B=0.1T exists in the space in direction perpendicular to the plane of the frame as shown in figure.Find the magnitude and direction of the magnetic forces on the four sides of the frame.
View SolutionA circular conductor of uniform resistance per unit length, is connected to a battery of 4 V. The total resistance of the conductor is 4ω. The net magnetic field at the centre of the conductor is

View SolutionFive point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
View SolutionA cell is connected between two points of a uniformly thick circular conductor and i1andi2 are the currents flowing in two parts of the circular conductor of radius a The magnetic field at the centre of the loop will be
View Solution
