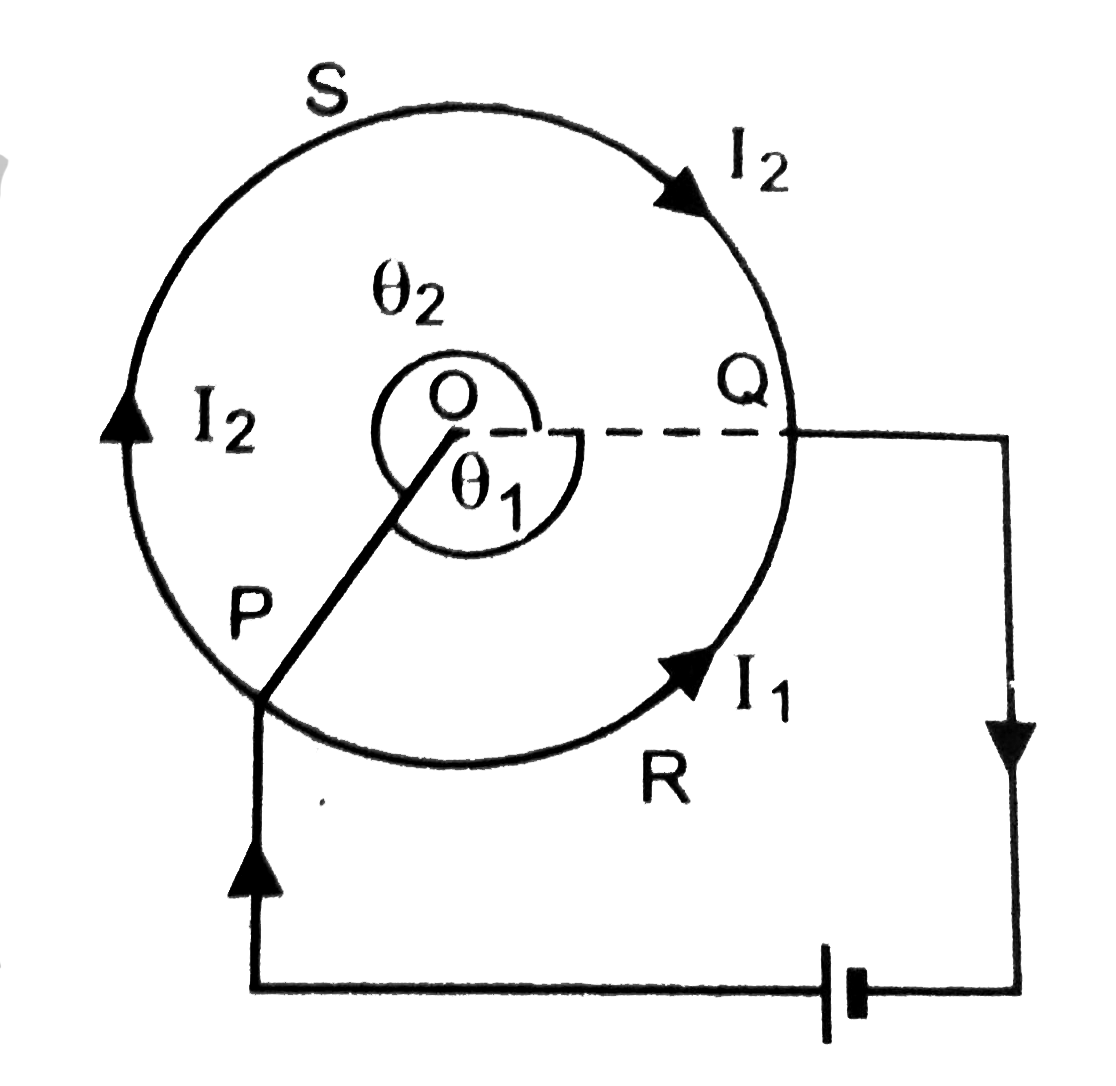
A cell is connected between two points of a uniformly thick circular conductor and i1andi2 are the currents flowing in two parts of the circular conductor of radius a The magnetic field at the centre of the loop will be
zero
μ04π(I1−I2)
μ02a(I1+I2)
μ0a(I1+I2)
The correct Answer is:A
Let l1,l2 be the lengths of the two parts PRQ and PSQ of the conductor and ρ be the resistance per unit length of the conductor . The resistance of the portion PRQ will be R1=l1ρ

The resistance of the portion PSQ will be R2=l2ρ pot diff across P and Q=I1,R1=I2R2
I1l1ρ=I2ρ or I1l1=I2l2 ....(1)
Magnetic field induction at the centre O due to currents through circular conductors PRQ and PSQ will be
=B1−B2=μ02I1l1sin90∘r2−μ04πI2l2sin90∘r2=0
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - DISHA PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXERCISE - 1 : Concept Builder (Topic wise) (Topic 3 : Force and torque on current carrying conductor and moving coil Galvanometor )
14 Videos
- MOTION IN A STRAIGHT LINEBOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise-2
30 Videos
- NUCLEIBOOK - DISHA PUBLICATIONCHAPTER - NUCLEIEXERCISE - EXERCISE - 2 (CONCEPT APPLICATOR)
30 Videos
Similar Questions
Two long straight conductors are connected radially to two arbitary points A and B of a circular conductor. Calculate the magnetic field at the center of the coil.
View SolutionAn infinitely long straight conductor is bent into the shape as shown in figure. It carries the current I and radius of the circular loop is a, then the magnetic field at the centre of the loop is ______
View Solution
Knowledge Check
A cell is connected between two points of a uniformly thick circular conductor. The magnetic field at the centre of the loop will be
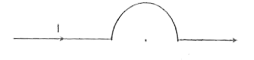
(Here i1 and i2 are the currents flowing in the two parts of the circular conductor of radius 'a' and μ0 has the usual meaning)AZeroBμ02a(i1−i2)Cμ02a(i1+i2)Dμ0a(i1+i2)A long straight conductor carrying a current i is bent to form an almost complete circular loop of radius r on it. The magnetic field at the centre of the loop
 Ais directed into the paperBis directed out of the paperChas magnitude μ0i2r(1−1π)Dhas magnitude μ(0)i2r(1+1π)
Ais directed into the paperBis directed out of the paperChas magnitude μ0i2r(1−1π)Dhas magnitude μ(0)i2r(1+1π)A part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
 Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)
Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)
A part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

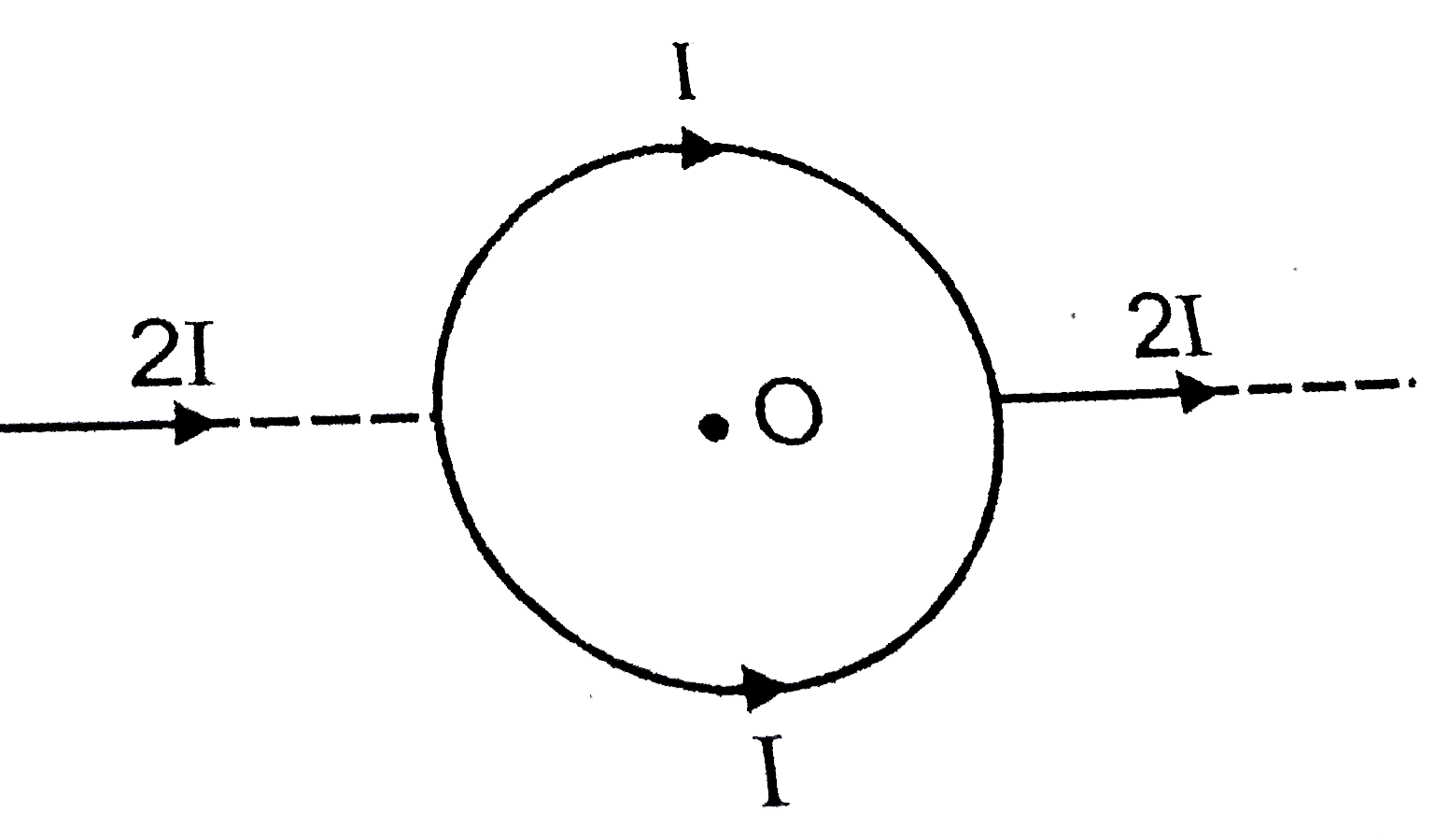
View SolutionAn infinite straigh conductor carrying current 2 I is split into a loop of radius r as shown in fig. the magnetic field at the centre of the coil is
View SolutionA cell is connected across two points P and Q of a uniform circular conductor, figure. Prove that the magnetic field at its centre O will be zero.
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View SolutionAs shown in figure a cell is connected across two points A and B of a uniform circular conductor of radius r. Prove that the magnetic field induction at its centre O will be zero.
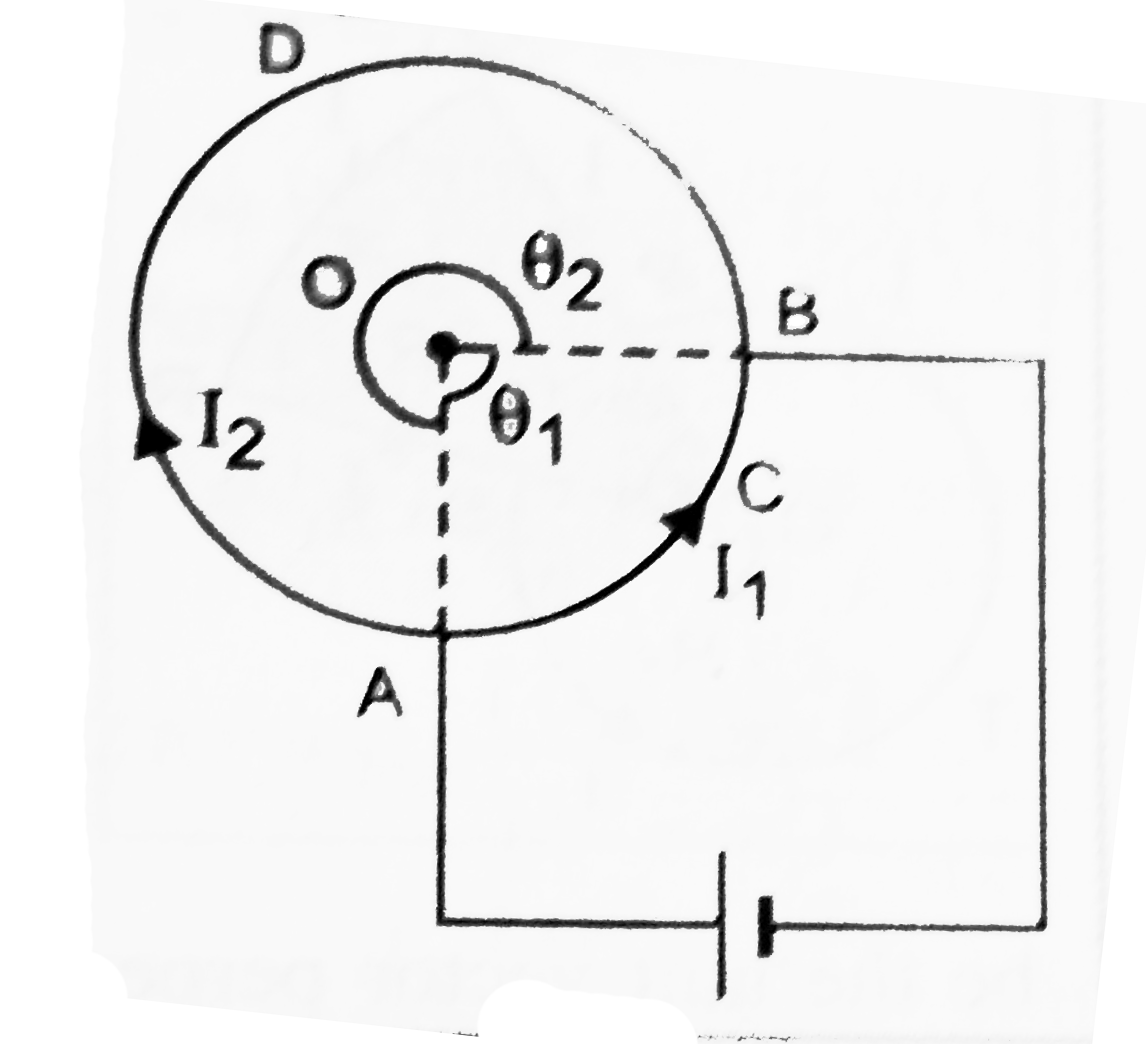
View Solution
