On meter length of wires carriers a constant current. The wire is bent to from a circular loop. The magnetic field at the centre of this loop is B. The same is now bent to form a circular loop of smaller radius to have four turns in the loop. The magnetic field at the centre of this loop B. The same is now bent to form a circular loop of smaller radius of have four turns in the loop. The magnetic field at the centre of this new loop is
B2
4B
B4
16B
The correct Answer is:d
To solve the problem, we will analyze the magnetic field produced by a circular loop of wire carrying a current.
1. Understanding the Initial Setup:
- We have a wire of length 1 meter carrying a constant current, which is bent to form a circular loop.
- The magnetic field at the center of this loop is given as B.
2. Magnetic Field Formula:
- The magnetic field B at the center of a circular loop of radius R with N turns and carrying current I is given by the formula:
B=μ0NI2R
- Here, μ0 is the permeability of free space.
3. First Loop:
- For the first loop, we have N=1 (one turn) and the length of the wire is 2πR=1 meter.
- Therefore, we can express the radius R as:
R=12π
- Substituting N=1 into the magnetic field formula gives:
B=μ0I2R
4. Second Loop:
- The wire is now bent to form a smaller circular loop with 4 turns.
- Let the new radius be R′. The total length of the wire remains the same, so:
2πR′=4×2πR
- This simplifies to:
R′=R4
5. Magnetic Field for the Second Loop:
- Now, substituting N=4 and R′=R4 into the magnetic field formula:
B′=μ0(4)I2R′=μ0(4)I2×R4=μ0(4)I×42R=16μ0I2R
- Since B=μ0I2R, we can express B′ in terms of B:
B′=16B
Final Answer:
The magnetic field at the center of the new loop with 4 turns is 16B.
- We have a wire of length 1 meter carrying a constant current, which is bent to form a circular loop.
- The magnetic field at the center of this loop is given as B.
- The magnetic field B at the center of a circular loop of radius R with N turns and carrying current I is given by the formula:
B=μ0NI2R
- Here, μ0 is the permeability of free space.
- For the first loop, we have N=1 (one turn) and the length of the wire is 2πR=1 meter.
- Therefore, we can express the radius R as:
R=12π
- Substituting N=1 into the magnetic field formula gives:
B=μ0I2R
- The wire is now bent to form a smaller circular loop with 4 turns.
- Let the new radius be R′. The total length of the wire remains the same, so:
2πR′=4×2πR
- This simplifies to:
R′=R4
- Now, substituting N=4 and R′=R4 into the magnetic field formula:
B′=μ0(4)I2R′=μ0(4)I2×R4=μ0(4)I×42R=16μ0I2R
- Since B=μ0I2R, we can express B′ in terms of B:
B′=16B
The magnetic field at the center of the new loop with 4 turns is 16B.
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following
4 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
A wire of length l carries a steady current. It is bent first to form a circular plane loop of one turn. The magnetic field at the centre of the loop is B. The same length is now bent more sharply to give a double loop of smaller radius. The magnetic field at the centre caused by the same is
View SolutionA long wire carrying a steady current is bent into a circular loop of one turn. The magnetic field at the centre of the loop is B. it is then bent into a circular coil of n turns. The magnetic field at the centre of this coil of n turns will be
View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionFind the magnetic field at the centre of the circular loop shown in figure.

View SolutionA wire of length 'I' is bent into a circular loop of radius R and carries a current I. The magnetic field at the centre of the loop is 'B '. The same wire is now bent into a double loop. If both loops carry the same current I and it is in the same direction, the magnetic field at the centre of the double loop will be
View SolutionA long wire carries a steady curent . It is bent into a circle of one turn and the magnetic field at the centre of the coil is B. It is then bent into a circular loop of n turns. The magnetic field at the centre of the coil will be
View SolutionA long wire carries a steady curent . It is bent into a circle of one turn and the magnetic field at the centre of the coil is B. It is then bent into a circular loop of n turns. The magnetic field at the centre of the coil will be
View SolutionThe magnetic field at the centre of the circular loop as shown in Fig. when a single wire is bent to form a circular loop and also extends to form straight sections is
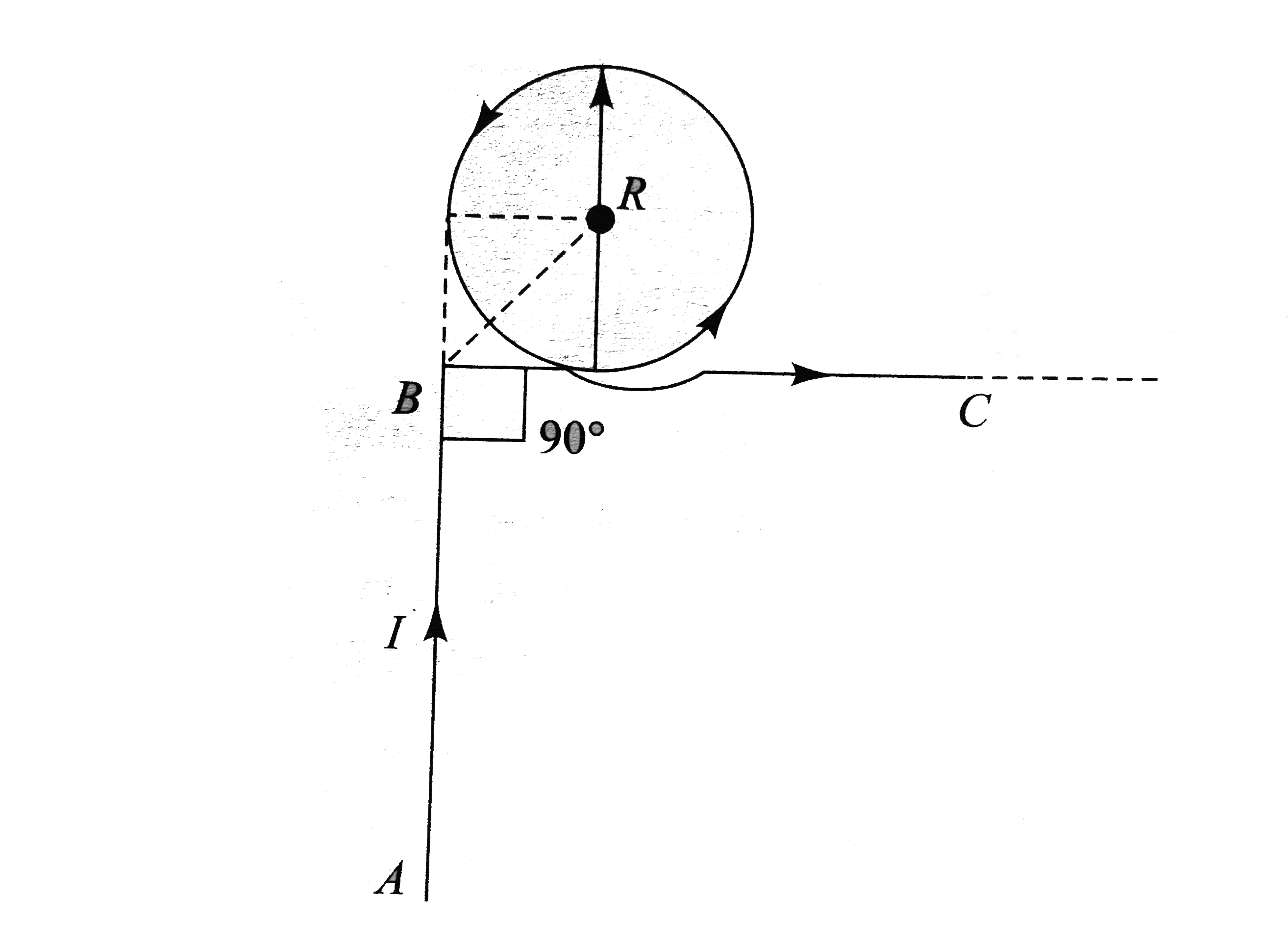
View SolutionA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View Solution
