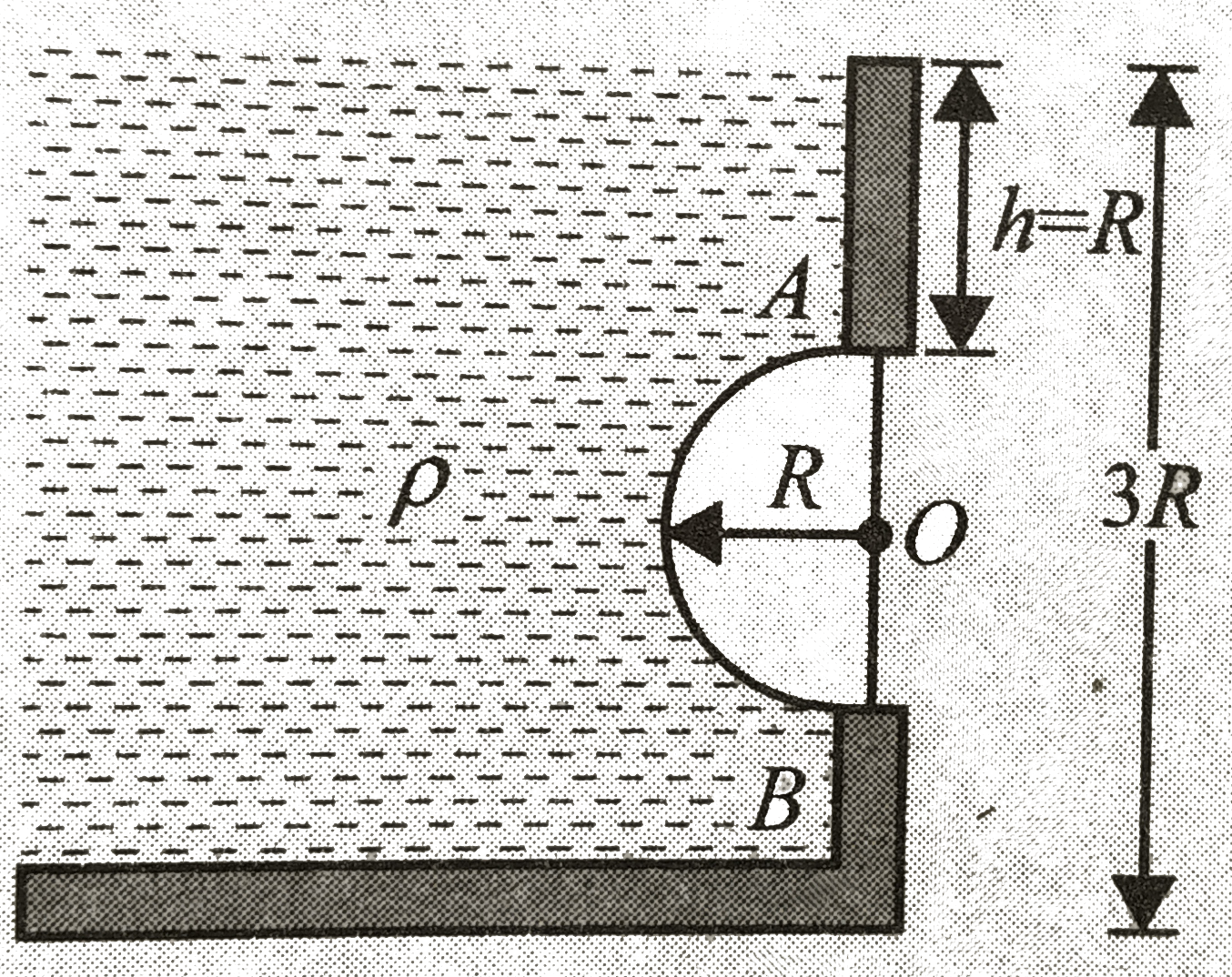
On removing a hemispherical part from the bottom of a cylinder, the mass and volume of cylinder become M and v. The remaining cylinder is suspended by a string in a liquid of density σ as show in figure. Calulate the force exerted by the liquid at the bottom of cylinder. 
W=Weight of liquid displaced by cylinder
If σ= density of liquid
Then W=Vσg
Thrust on upper surface of cylinder due to height h of liquid.
F=P×πR2=hσπR2
Total upward force exerted by liquid on cylinder F∘=W+F
=Vσg+hσgπR2
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Very Short Answer Questions)54videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Revision Exercise (Additional Questions)3videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Short Answer Type Questions)5videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)12videos
MATHEMATICAL TOOLS
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test15videos
MOTION IN A PLANE
Similar Questions
A conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is
View SolutionTo what height should a cyclindrical vessel be filled with a homogeneous liquid to make the force with which the liquid pressure on the sides of the vessel equal to the force exerted by the liquid on the bottom of the vessel ?
View Solution
Knowledge Check
- Question 1 - Select One
A hemispherical portion of a radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at a depth of h below the liquid surface. THe force on the bottom of the cylinder by the liquid is
AM gBMg−Vρ gCMg+ΠR2hgρDρg(V+ΠR2h) - Question 2 - Select One
A hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder bby the liquid is
AMgBMg - h ρ gCMg+πR2hρgDρg(V+πR2h) - Question 3 - Select One
A hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is
AMgBMg-VdgCMg+πR2hdgDdg(V+πR2h)
A hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is
View SolutionA conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is
View SolutionFigure shows a semi-cylindrical massless gate pivoted at the point O holding a stationary liquid of density ρ. The length of the cylinder is l. Calculate, the horizontal force exerted by the liquid on the gate.
View SolutionA cylinder of mass m and density ρ hanging from a string is lowered into a vessel of cross-section area s containing a liquid of density σ(<ρ) unit it is fully immersed. The increase in pressure at the bottom of the vessel is
View SolutionA uniform cylinder of mass m, length l and cross sectional area A is suspended with its vertical from a fixed point, with the help of a massless spirng of force constant (K), The cylinder is then submerged in a liquid of density p. At equilibrium the cylinder remains submerged in the liquid with 1/4th of its volume outside the liquid, as shown in the figure. The elongation of hte spring at this point is x0. WHen the cylinder is given a slight downward push into the liquid and then released, its starts oscillating with vertical S.H.M. of small amplitude.
Time period of vertical S.H.M of the cylinder isView Solution