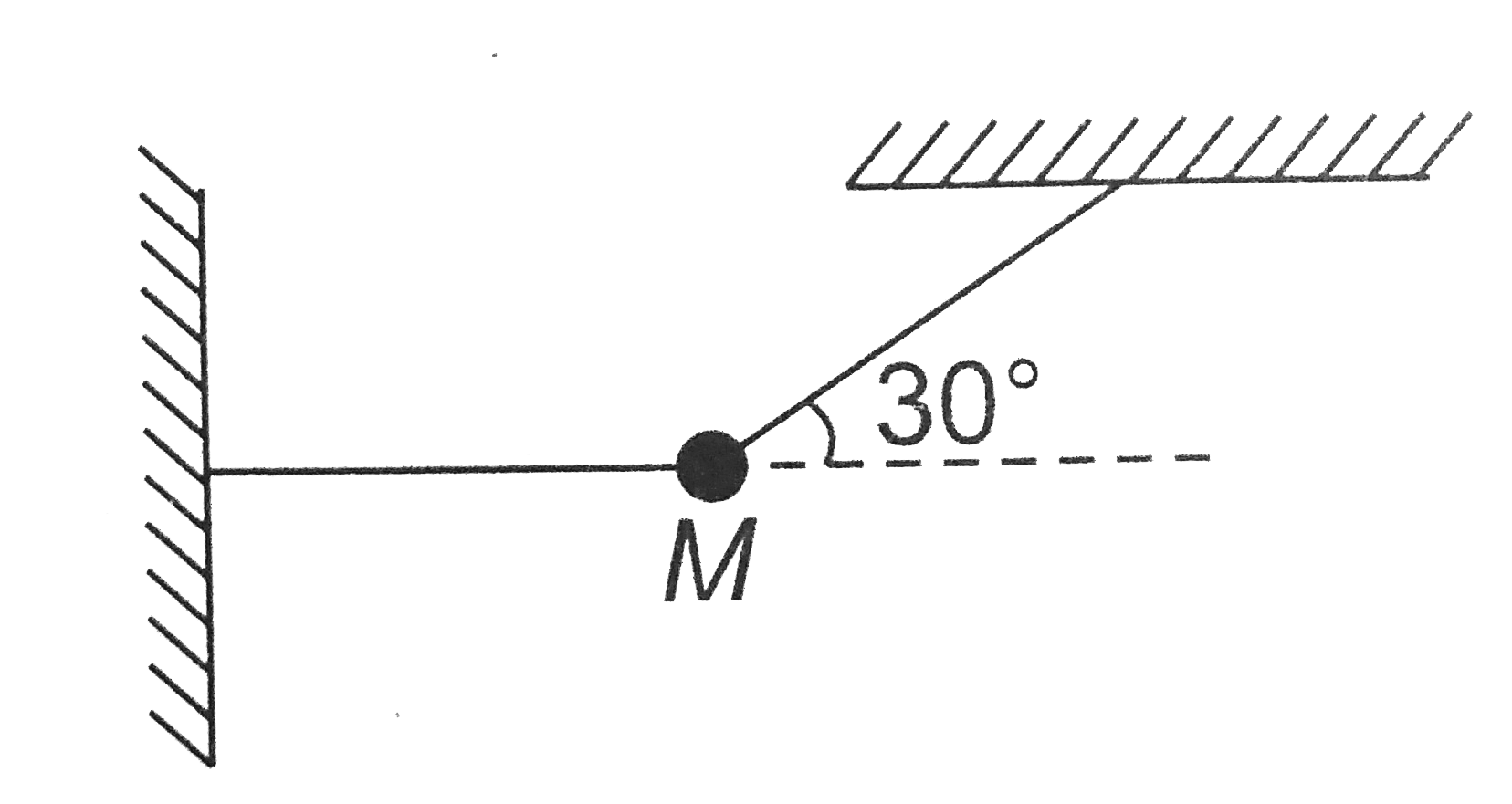
One end of a light string is fixed to the celling and the other end is tied to the wall. A body of mass 500 g is suspended from that string in such a way that the part of the string towards the wall remains horizontal and the portion towards the ceiling makes an angle of 30∘ with the ceiling. Find the tension on the two parts of the string. Solution in Bengali
Let the positive y-axis be vertically upwards and the x-axis be horizontal Fig. Let T1= tension in the horizontal part of the string, T2 = tension in the other part of the string, W = weight of the suspended body= 500×981dyn.
Sum of the components of the force along y-axis =T2sin30∘-W
Sum of the components of the forces along x-axis
T1−T2cos30∘
As the system is in equilibrium,
T2sin30∘−W=0 ⋯(1)
T1−T2cos30∘=0 ⋯(2)
From (1),
12T2=W
or, T2=2W
=2×500×981dyn=2×500×981105N=9.81N
From (2),
T1=T2cos30∘=9.81×cos30∘=8.5N.

Topper's Solved these Questions
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
18 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - EXERCISE (Multiple Choice Questions )
14 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER
16 Videos
- SUPERPOSITION OF WAVESBOOK - CHHAYA PUBLICATIONCHAPTER - SUPERPOSITION OF WAVESEXERCISE - CBSE Scanner
14 Videos
Similar Questions
Describe the moment of a force about a point as a vector quantity.
View SolutionTwo particles, initially at rest due to their mutual attraction move towards each other. When their relative velocity becomes v , velocity of the centre of mass of the system becomes
View SolutionExplain the relation in phase between displacement velocity and acceleration in SHM, graphically as well as theoretically.
View SolutionA progressive wave is given by y(x,l)=Bcos(300t−0.15x) where x and y are in cm and t in second . What is the (i) direction of propagation, (ii) wavelength , (iii) frequency, (iv) wave speed and (v) phase difference between two points 0 . 2 m apart ?
View SolutionA body of mass mis suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionA mass M is hung with a light inextensible string. Tension in horizontal part of string is.
View SolutionA 1 m long rope, having a mass of 40 g , is fixed at one end and is tied to a light string at the other end. The tension in the string in 400 N . Find the wavelength in second overtone (in cm ).
View Solution1 क्रिगा द्रव्यमान का एक गोला 50 सेमी लम्बी डोरी के एक सिरे पर बँधा हैं जिसका दूसरा सिरा छत से बँधा हैं । गोला 30 सेमी त्रिज्या के क्षैतिज वृत्त में गति करता हैं । इस शंकु लोलक का आवर्तकाल तथा डोरी में तनाव ज्ञात कीजियें । (g = 10 मीटर/सेकण्ड^(2))
View SolutionA small ball is suspended by a string from the ceiling of a car. As the car accelerates at a rate ‘a’ the string makes an angle 'a' with the vertical in equilibrium. Then the tension in the string is :
View SolutionA body of mass 13 kg is suspended by two strings of length 5 cm and 12 cm . The other ends of the strings are tied to two pegs 13 cm apart along a horizontal line . The tensions in the strings are
View SolutionA small mass is suspended by a string from the ceiling of a car. As the car accelerates at a rate 'a' the string makes an angle theta with the vertical. Then the tension in the string
View SolutionA small mass is suspended by a string from the ceiling of a car. As the car accelerates at a rate 'a' the string makes an angle theta with the vertical. Then the tension in the string
View SolutionA small mass is suspended by a string from the ceiling of a car. As the car accelerates with an acceleration a horizontal road, the angle made by the string with the vertical is
View SolutionA body of mass m is suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionA small mass is suspended by a string from the ceiling of a car. As the car accelerates at a rate 'a' the string makes an angle θ with the vertical. Then the tension in the string
View Solution
