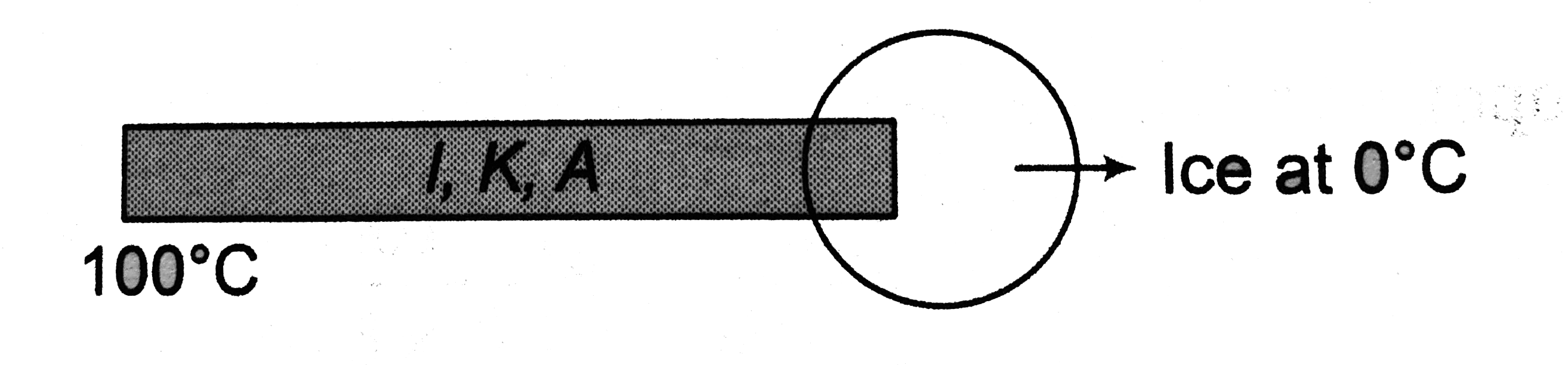
One end of the rod of length l, thermal conductivity K and area of cross-section A is maintained at a constant temperature of 100∘C. At the other end large quantity of ice is kept at 0∘C . Due to temperature difference, heat flows from left end to right end of the rod. Due to this heat ice will start melting. Neglecting the radiation losses find the expression of rate of melting of ice.
 .
.
The correct Answer is:A, D
Putting,
(dQdt)conduction=(dQdt)calorimetry
∴TDR=L⋅dmdt
⇒dmdt=TDRL
So, this is the desired expression of dmdt.
In the above expression,
TD=100∘C,R=lKA
and L = latent heat of fusion.
Topper's Solved these Questions
- CALORIMETRY & HEAT TRANSFERBook:DC PANDEYChapter:CALORIMETRY & HEAT TRANSFERExercise:Example Type 3
Explore 1 Video
- CALORIMETRY & HEAT TRANSFERBook:DC PANDEYChapter:CALORIMETRY & HEAT TRANSFERExercise:Example Type 4
Explore 4 Videos
- CALORIMETRY & HEAT TRANSFERBook:DC PANDEYChapter:CALORIMETRY & HEAT TRANSFERExercise:Example Type 1
Explore 4 Videos
- BASIC MATHEMATICSBook:DC PANDEYChapter:BASIC MATHEMATICSExercise:Exercise
Explore 13 Videos
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEYChapter:CALORIMETRY AND HEAT TRANSFERExercise:Medical entrance s gallery
Explore 38 Videos
Similar Questions
One end of a copper rod of length 1 m and area of cross - section 400×(10−4)m2 is maintained at 100∘C. At the other end of the rod ice is kept at 0∘C. Neglecting the loss of heat from the surrounding, find the mass of ice melted in 1h. Given, KCu=401W/m−KandLf=3.35×(105)J/kg.
View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View Solution
Knowledge Check
One end of conducting rod is maintained at temperature 50∘C and at the other end ice is melting at 0∘C. The rate of melting of ice is doubled if:
Athe temperature is made 200∘C and the area of cross-section of the rod is doubledBthe temperature is made 100∘C and the length of the rod is made four timeCarea of cross-section of the rod is halved and length is doubled.Dthe temperature is made 100∘C and area of cross-section of rod and length both are doubled.The end of two rods of different materials with their thermal conductivities, area of cross-section and lengths all in the ratio 1:2 are maintained at the same temperature difference. If the rate of flow of heat in the first rod is 4cal/s. Then, in the second rod rate of heat flow in cal/s will be
A1B2C8D16One end of a metal rod of length 1.0 m and area of cross section 100cm2 is maintained at . 100∘C. If the other end of the rod is maintained at 0∘C , the quantity of heat transmitted through the rod per minute is (Coefficient of thermal conductivity of material of rod =100W/m−K)
A3×103JB6×103JC9×103JD12×103J
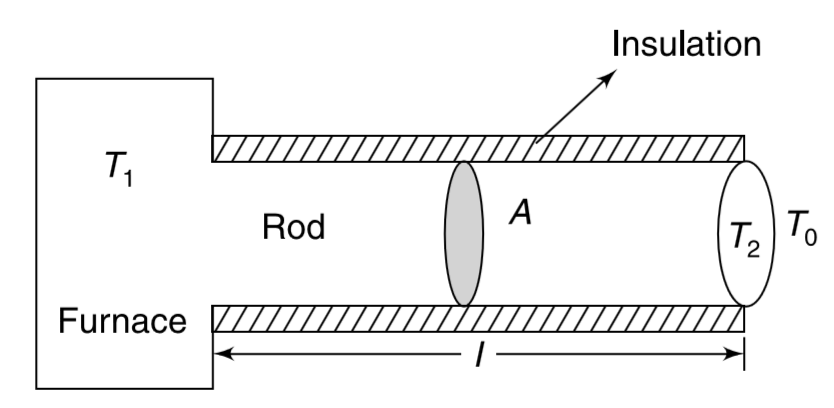
A cylindrical rod of length l, thermal conductivity k and area of cross section A has one end in a furnace maintained at constant temperature. The other end of the rod is exposed to surrounding. The curved surface of the rod is well insulated from the surrounding. The surrounding temperature is T0 and the furnace is maintained at T1=T0+ΔT1. The exposed end of the rod is found to be slightly warmer then the surrounding with its temperature maintained T2=T0+ΔT2[ΔT2<<T0]. The exposed surface of the rod has emissivity e. Prove that ΔT1 is proportional to ΔT2 and find the proportionality constant.
View SolutionThe ends of the two rods of different materials with their lengths, diameters of cross-section and thermal conductivities all in the ratio 1 : 2 are maintained at the same temperature difference. The rate of flow of heat in the shorter rod is 1cals−1. What is the rate of flow of heat in the larger rod:
View SolutionTwo rods of length l and 2l thermal conductivities 2K and K are connected end to end. If cross sectional areas of two rods are eual, then equivalent thermal conductivity of the system is .
View SolutionTwo ends of area A of a uniform rod of thermal conductivity k are maintained at different but constant temperatures. At any point on the rod, the temperature gradient is dTdl. If I be the thermal current in the rod, then:
View SolutionThe two ends of a uniform rod of thermal conductivity k are maintained at different but constant temperatures. The temperature gradientat any point on the rod is dθdl(equal to the difference in temperature per unit length). The heat flow per unit time per unit cross-section of the rod is l then which of the following statements is/are correct:
View Solution